物理中干涉现象的前世今生（大学物理版）

导言：这个知识块可谓是让广大学生同胞包括我恨铁不成钢，所以本人想通过讲述它的前因后果来让大家以及自己能对干涉现象有更生蹭的了解，同时激发自己对于物理的兴趣。

地图：接着让我们来了解一下那些是难点。干涉现象的概念很好理解，就是两个波才传播过程中相互作用所引发的一系列作用效果，而波可以有声波、光波以及水波，所以概念理解方面不算难点。难点1：计算，计算什么？计算波程差以及干涉相长点以及干涉相消点。难点2：多模型化，干涉现象可以按波的种类分类研究，如光波以及水波；也可以按照研究方法分，如分波面法以及分振幅法，同时一个研究方法同时还会有许多实例，如杨氏双缝干涉、薄膜干涉，劈尖干涉以及牛顿环，可以说是错综复杂。但我们的策略是农村包围城市，通过一些简单的地方与难点建立联系，把难点与难点分离，从而达到自己的战略目的。

讲述：

首先，上一下干涉的图。

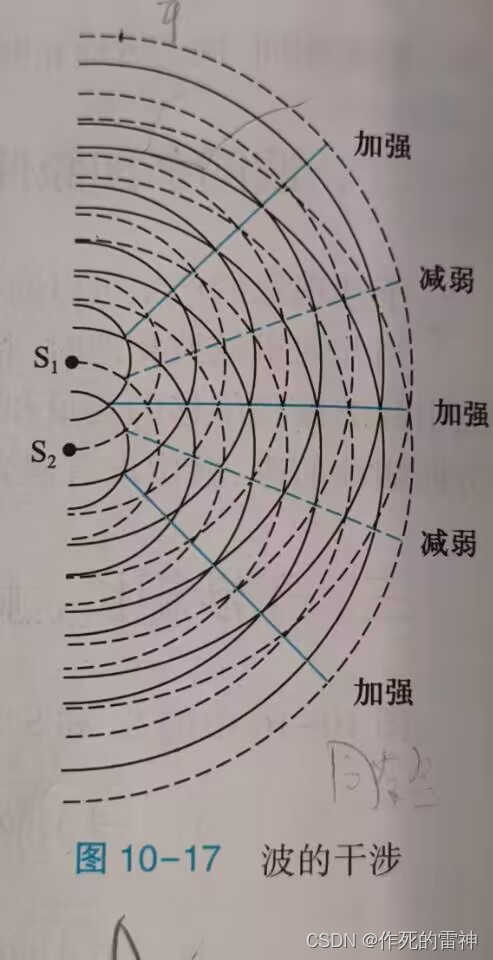
差不多对干涉已经有了一个自己的印象了，两个波相互作用所引发的效果(干涉图样)，接着我们来看一下这个事情的因，也就是条件：1.两个波同向振动。2.两个波频率相同。3.两个波相位差保持不变。4.两个波的振幅相差不太大（在干涉条纹中使用）。不过我们现在先不讲深了，因为再讲就涉及到计算了，我们先把多模型化（难点2）给解决了。我们先看一下分波面法领域下的杨氏双缝干涉

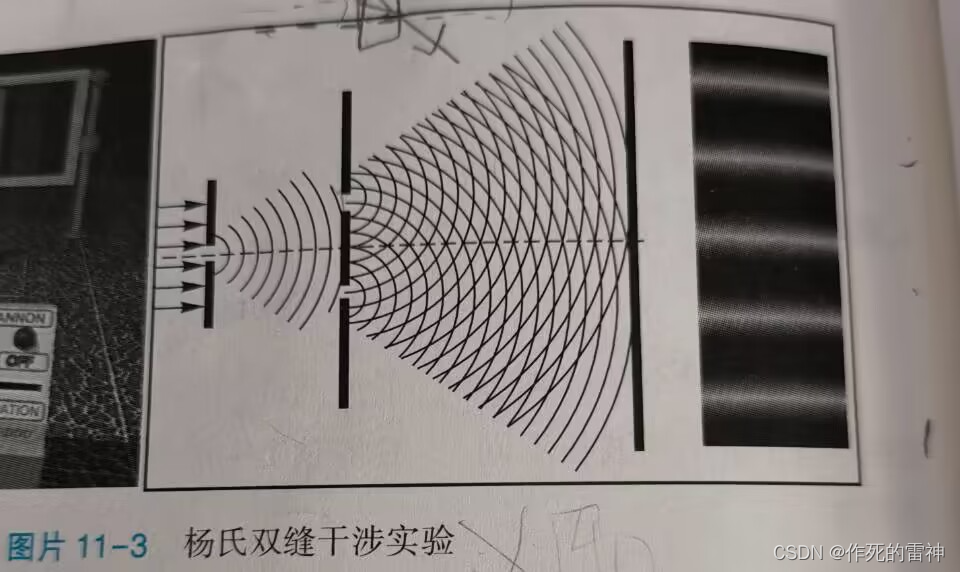
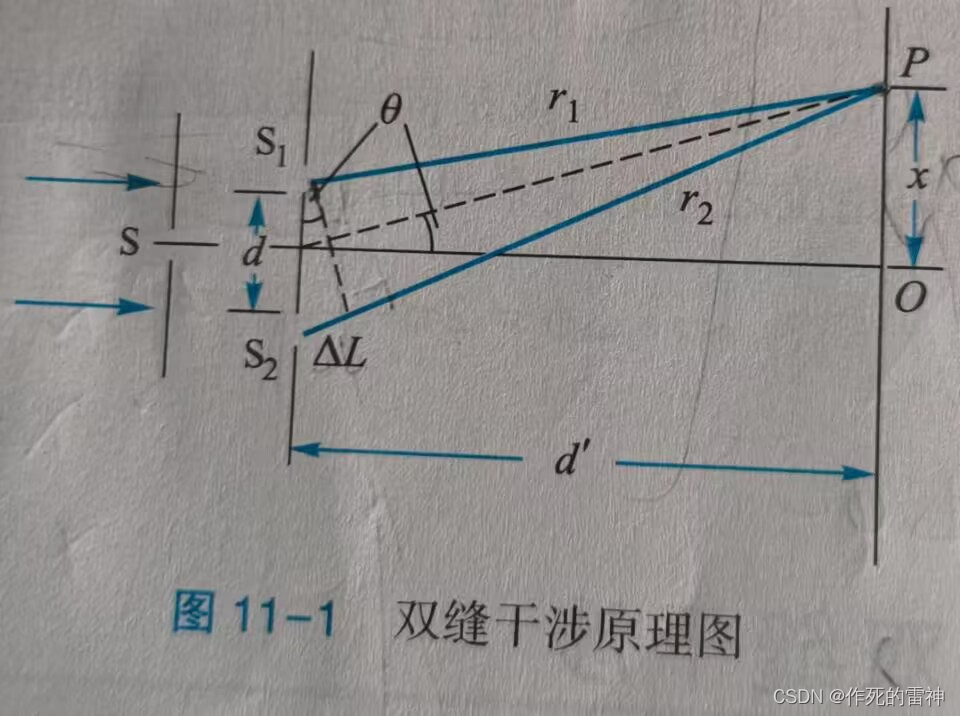
一样的套路，只不过就是将水波换成光波了，不过它和水波来比多了一个原理图，而原理图是拿来为光程差服务的，先不讲深了，具体计算还是拿到下文。光波的形成条件都是一样的，都是上面四条。这里还要注意的是不用把原理图中的那个线想成光波，光波是左图，和线没有关系，那个线只是表示波源到P点的距离。接着，我们来挑战一下分振幅法。

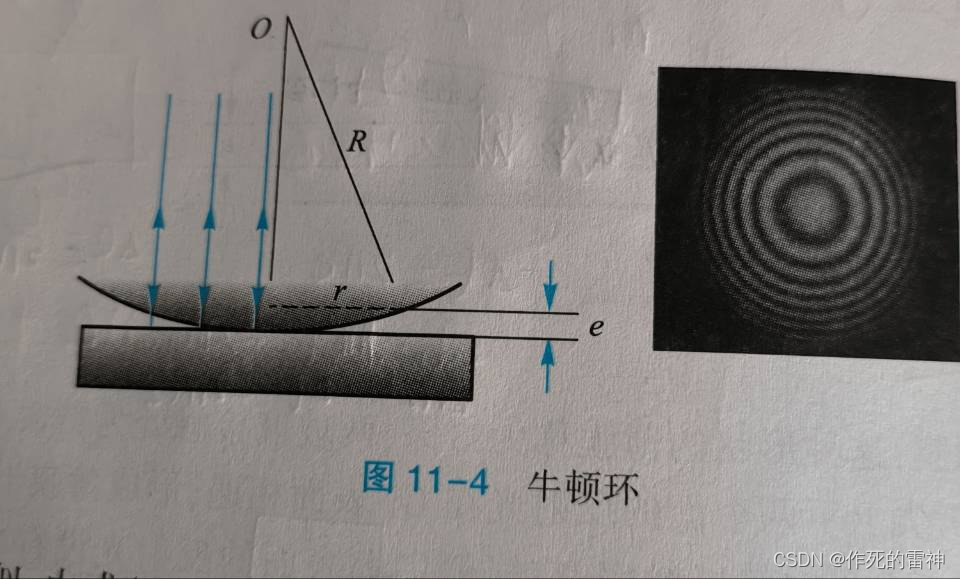
分振幅法有三个模型，分别如上图所示，而这三张图也都是拿来为光程差服务的，而光程差的复杂也会导致波的叠加的计算复杂。到此为止，我们已经把难点二，多模型化给解决了，知识框架已经搭建起了，这样子的话，只要我们掌握了一个类型的计算，那么其它类型的直接类比过去就可以直接解决了。接着我们要向深处探索。

回到普通干涉的图，我们先从因入手，那么就是这四个条件是否都是缺一不可，我们先拿出波函数来分析一下：y = Acos(w(t-x/u)+φ),为了让两个波形成的图像稳定且有规律，必然会让两个波的频率，也可以说角速度相同（条件1），而且还要保证波的传播速度相同，也就是u，相同，而以上两个条件则会造成相位差保持恒定（条件2），接着是振动方向一样（条件3），这个是确保两个波不会相互抵消，至于振幅相差不大（条件4）则是为了使图样明显。这样我们就可以分离出两个波的方程，波1：y1 = A1cos(w(t - x1/u) + φ1), 波2：y = A2cos(w(t - x2/u) + φ2)（注意条件中没有说振幅必须相同或者初相位为0）。这样子我们就有了研究波的叠加的资本了，不过为了方便研究，我们先要把两个方程改造一下，即波1：y1 = A1cos(2π(t/T) - 2π(x1/l) + φ1）波2：y2 = A2cos(2π(t/T) - 2π(x2/l) + φ2），那么什么时候振动加强，什么时候振动减弱呢？我们从相位差入手，当deltaφ=2kπ时，振动加强，而当deltaφ = （2k+1）π 时，振动抵消（减弱），而1与2的deltaφ = φ1 - φ2 - 2π（x1-x2) / l，为了研究方便，我们令φ1 - φ2 = 0，就有了 deltaφ = 2π（x1-x2) / l（注意这里因为余弦函数的周期性，所以不用考虑±号），接着我们来看振动加强点，令2π（x1 - x2）/ l = 2kπ，则有x1 - x2 = 2k*(l/2) = kl(前一个式子主要是与2kπ进行对照)，而振动减弱点,令2π（x1 - x2）/ l = (2k+1)π，则有x1 - x2 = (2k+1)*(l/2) = (k + 1/2) *l。于是我们就彻底的把干涉给搞懂了，接下来就只剩类比了。

总结一下计算过程，我们先从波函数入手推导出两个波的公式，接着再通过波程差以及函数规律推导出振动加强点以及振动减弱点所要满足的条件，前者为 deltax = 2k *(l/2) = kl,后者为 deltax = (2k+1)*(l.2) = (k+1/2)l。然后接下来我们在其它具体模型中要干的无非就是把deltax用其他的所给条件给替换点，并推导出改模型中振动加强以及振动减弱的条件即可。把它当成例题就行。不过下文中deltax都会用deltal表示。

第一题：杨氏双缝干涉。

该题中求deltax的难处就在于自己对特殊几何以及相似三角形的理解，同时还涉及到一些数学分析的知识，比如当sita 趋近于0时，sinsita = tansita。不过没有关系，我们只要一一对应就行了，d对应d’，然后deltal 对应 x，不难得出，d:d' = deltal:x,从而得到我们想要的deltal = x * (d/d') =kl, 这里因为x在实验中比较明显，我们就直接用deltal来表示x，即x = deltal *(d'/d)，当 x = （2k)(l/2) * (d'/d)时振动加强，当 x = (2k + 1)（l/2）*（d’/d）振动减弱。根据x的特性，我们得到新名词条纹间距，即亮条纹与亮条纹之间的距离（暗条纹也行）， distance = l*(d'/d)。

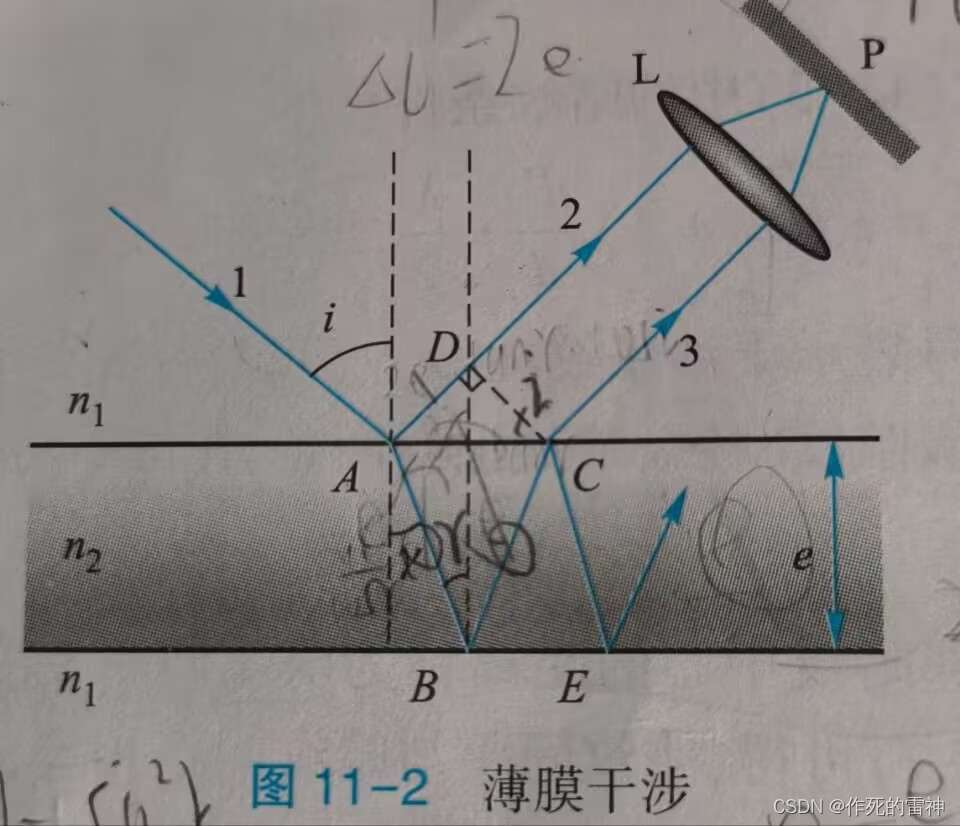
第二题：薄膜干涉。

这个题和上面那个题来比就难上不少，因为它还需要二个前置知识，光的折射定律：n1sinsita1 = n2sinsita2, 半波损失：n1

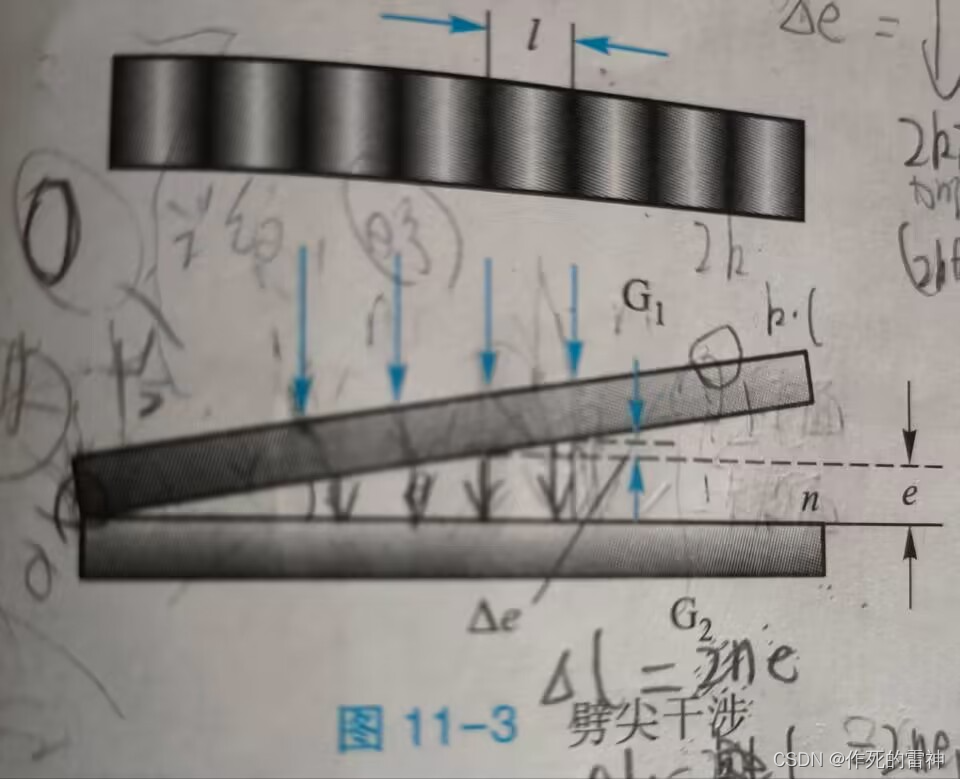
第三题：劈尖干涉

这个题直接结束,根据第二题有 deltal = 2n2e + (l/2).然后是，e = (deltal - l/2)/(2*n2).和条纹间距一样，我们可以得出条纹间距的薄膜厚度为deltae = l / (2n2),然后直捣黄龙，条纹间距deltae = l / 2n2cosγ 。

第四题：牛顿环

屑笔主不会做的说^