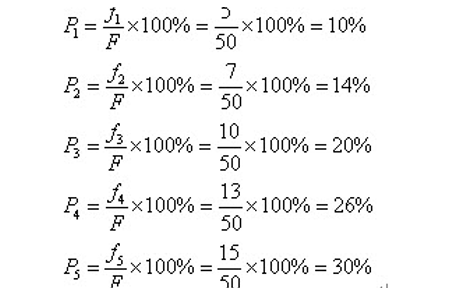初探考试系统主观题评分的算法

问题：
1、主观题的考查内容多为学生发挥为主，很难给出一个固定的考试答案，现有的人工阅卷中也多以知识点为得分进行处理；
2、主观题涉及的知识点多而且很杂，汉语相对其他语言来说句子的成分更加的复杂多变，词汇量很大，有很多的近义词、同义词，同一个语句在不同的语境中有不同含义，阅卷时对知识点的分类整理往往工作量非常的大；
3、评卷时，如何提高考生的答案与标准答案的相似度比较准确度也是一个极大的问题。


思路：
1 主观题人工阅卷思路与步骤 
   教师在人工批改主观题如名词解释与简答题时，一般按照如下
 
 (1)确定主观题标准答案的得分点，每一个得分点所对应的关键
 
 (2)教师开始对学生答案进行评阅，将学生答案中出现的词汇与
如果两者相同或是近义词，那么学生
 
 (3)为了防止学生在答题时只答关键词，而出现语句不通的情况，
也会查看学生答案语句的组织是
 
 2 主观题自动评分算法设计思路 
   人具有自己的思想，能独立思考问题，并发执行许多事情，但
它只能模拟人工阅卷过程。




解决方法：
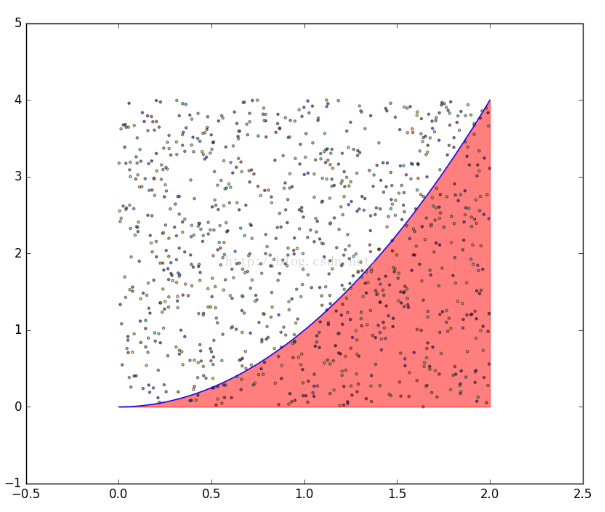
1、蒙特卡罗算法表示采样越多，越近似最优解。举个例子，假如筐里有100个苹果，让我每次闭眼拿1个，挑出最大的。于是我随机拿1个，再随机拿1个跟它比，留下大的，再随机拿1个……我每拿一次，留下的苹果都至少不比上次的小。拿的次数越多，挑出的苹果就越大，但我除非拿100次，否则无法肯定挑出了最大的。这个挑苹果的算法，就属于蒙特卡罗算法。告诉我们样本容量足够大，则最接近所要求解的概率。
1）这种思想来源于阿尔法狗的算法；
2）这个也是最接近人工模拟人的思维来评分；
3） 蒙特卡洛方法并没有什么高深的理论支撑，如果一定要说有理论也就只有概率论或统计学中的大数定律了。蒙特卡洛的基本原理简单描述是先大量模拟，然后计算一个事件发生的次数，再通过这个发生次数除以总模拟次数，得到想要的结果。比如投3个骰子，计算3个骰子同时是6的概率，可以模拟投N次（随机样本数），统计同时是6出现的次数C，然后C除以N即是计算结果。


（求的是近似解，样本数越大越接近于真实值）
2、蒙特卡洛方法与遗传算法、粒子群算法等智能优化算法有相似之处，比如都属于随机近似方法，都不能保证得到最优解等，但它们也有着本质的差别。一是层次不一样，蒙特卡洛只能称之为方法，遗传算法等则属于仿生智能算法，比蒙特卡洛方法要复杂。二是应用领域不同，蒙特卡洛是一种模拟统计方法，如果问题可以描述成某种统计量的形式，那么就可以用蒙特卡洛方法来解决；遗传算法等则适用于大规模的组合优化问题（选址问题、排班问题、管理调度、路线优化）等，以及复杂函数求最值、参数优化等。


3、遗传算法：（Genetic Algorithm, GA）起源于对生物系统所进行的计算机模拟研究。它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法，能在搜索过程中自动获取和积累有关搜索空间的知识，并自适应地控制搜索过程以求得最佳解。
1）实现过程：
遗传算法的实现过程实际上就像自然界的进化过程那样。首先寻找一种对问题潜在解进行“数字化”编码的方案。（建立表现型和基因型的映射关系）然后用随机数初始化一个种群（那么第一批袋鼠就被随意地分散在山脉上），种群里面的个体就是这些数字化的编码。接下来，通过适当的解码过程之后（得到袋鼠的位置坐标），用适应性函数对每一个基因个体作一次适应度评估（袋鼠爬得越高，越是受我们的喜爱，所以适应度相应越高）。用选择函数按照某种规定择优选择（我们要每隔一段时间，在山上射杀一些所在海拔较低的袋鼠，以保证袋鼠总体数目持平。）。让个体基因变异（让袋鼠随机地跳一跳）。然后产生子代（希望存活下来的袋鼠是多产的，并在那里生儿育女）。遗传算法并不保证你能获得问题的最优解，但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。（你不必去指导袋鼠向那边跳，跳多远。）而只要简单的“否定”一些表现不好的个体就行了。
2）物竞天择：
物竞天择－－适应性评分与及选择函数。


1.物竞――适应度函数（fitness function）


   自然界生物竞争过程往往包含两个方面：生物相互间的搏斗与及生物与客观环境的搏斗过程。但在我们这个实例里面，你可以想象到，袋鼠相互之间是非常友好的，它们并不需要互相搏斗以争取生存的权利。它们的生死存亡更多是取决于你的判断。因为你要衡量哪只袋鼠该杀，哪只袋鼠不该杀，所以你必须制定一个衡量的标准。而对于这个问题，这个衡量的标准比较容易制定：袋鼠所在的海拔高度。（因为你单纯地希望袋鼠爬得越高越好。）所以我们直接用袋鼠的海拔高度作为它们的适应性评分。即适应度函数直接返回函数值就行了。


2.天择――选择函数（selection）


    自然界中，越适应的个体就越有可能繁殖后代。但是也不能说适应度越高的就肯定后代越多，只能是从概率上来说更多。（毕竟有些所处海拔高度较低的袋鼠很幸运，逃过了你的眼睛。）那么我们怎么来建立这种概率关系呢？下面我们介绍一种常用的选择方法――轮盘赌（Roulette Wheel Selection）选择法。                                 


     比如我们有5条染色体，他们所对应的适应度评分分别为：5，7，10，13，15。


       所以累计总适应度为：


                                  


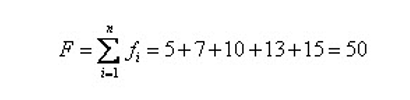
       所以各个个体被选中的概率分别为：



3、决策树算法的思想：
1）树以代表训练样本的单个结点开始。
2）如果样本都在同一个类．则该结点成为树叶，并用该类标记。
3）否则，算法选择最有分类能力的属性作为决策树的当前结点．
4）根据当前决策结点属性取值的不同，将训练样本数据集tlI分为若干子集，每个取值形成一个分枝，有几个取值形成几个分枝。匀针对上一步得到的一个子集，重复进行先前步骤，递4'I形成每个划分样本上的决策树。一旦一个属性出现在一个结点上，就不必在该结点的任何后代考虑它。
5）递归划分步骤仅当下列条件之一成立时停止：
①给定结点的所有样本属于同一类。
②没有剩余属性可以用来进一步划分样本．在这种情况下．使用多数表决，将给定的结点转换成树叶，并以样本中元组个数最多的类别作为类别标记，同时也可以存放该结点样本的类别分布，
③如果某一分枝tc，没有满足该分支中已有分类的样本，则以样本的多数类创建一个树叶。
6）构造方法：
决策树构造的输入是一组带有类别标记的例子，构造的结果是一棵二叉树或多叉树。二叉树的内部节点(非叶子节点)一般表示为一个逻辑判断，如形式为a=aj的逻辑判断，其中a是属性，aj是该属性的所有取值：树的边是逻辑判断的分支结果。多叉树(ID3)的内部结点是属性，边是该属性的所有取值，有几个属性值就有几条边。树的叶子节点都是类别标记。
由于数据表示不当、有噪声或者由于决策树生成时产生重复的子树等原因，都会造成产生的决策树过大。因此，简化决策树是一个不可缺少的环节。寻找一棵最优决策树，主要应解决以下3个最优化问题：①生成最少数目的叶子节点；②生成的每个叶子节点的深度最小；③生成的决策树叶子节点最少且每个叶子节点的深度最小。
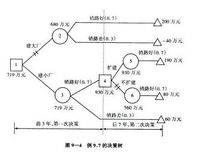
7）实例：为了适应市场的需要，某地准备扩大电视机生产。市场预测表明：产品销路好的概率为0.7；销路差的概率为0.3。备选方案有三个：第一个方案是建设大工厂，需要投资600万元，可使用10年；如销路好，每年可赢利200万元；如销路不好，每年会亏损40万元。第二个方案是建设小工厂，需投资280万元；如销路好，每年可赢利80万元；如销路不好，每年也会赢利60万元。第三个方案也是先建设小工厂，但是如销路好，3年后扩建，扩建需投资400万元，可使用7年，扩建后每年会赢利190万元。
各点期望：
点②：0.7×200×10+0.3×（-40）×10-600（投资）=680（万元）


决策树分析
点⑤：1.0×190×7-400=930（万元）
点⑥：1.0×80×7=560（万元）
比较决策点4的情况可以看到，由于点⑤（930万元）与点⑥（560万元）相比，点⑤的期望利润值较大，因此应采用扩建的方案，而舍弃不扩建的方案。把点⑤的930万元移到点4来，可计算出点③的期望利润值。
点③：0.7×80×3+0.7×930+0.3×60×（3+7）-280 = 719（万元）
最后比较决策点1的情况。由于点③（719万元）与点②（680万元）相比，点③的期望利润值较大，因此取点③而舍点②。这样，相比之下，建设大工厂的方案不是最优方案，合理的策略应采用前3年建小工厂，如销路好，后7年进行扩建的方案。
总结
上述的几种算法可谓是都可以使用，但是他们各有各自的优点，也都有自己的缺点。需要结合的使用，目前来说开发实现的难度还是很大的，毕竟国内还没有一个非常成熟的系统。目前AI盛行的时代，我想攻克只是时间啊的问题。我虽没有太大的思路，但是通过查询资料，个人觉得这几个算法还是比较靠谱的。路漫漫其修远兮。吾将上下而求索。