本文主要是介绍HoMM: Higher-order Moment Matching for Unsupervised Domain Adaptation读书笔记,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文是AAAI收录的一篇文章,与以往方法不同,其提出要对高阶特征进行域匹配,下面就简要介绍一下其思路。
摘要
最大限度地减小不同域间特征分布的差异是无监督域自适应最有前途的方向之一。从分布匹配的角度来看,现有的基于离散度的方法大多是针对二阶或更低阶的统计量设计的,而这些方法对非高斯分布的统计特性的表达是有限的。在这项工作中,我们探讨了使用高阶统计量(主要指三阶和四阶统计量)进行域匹配的好处。提出了一种高阶矩匹配(HoMM)方法,并将其扩展到复制核希尔伯特空间(RKHS)。特别地,本文提出的HoMM可以进行任意阶矩张量匹配,并证明了一阶HoMM等价于MMD,二阶HoMM等价于CORAL。此外,三阶和四阶矩张量匹配有助于实现全面的域对齐,因为高阶统计量可以近似更复杂的非高斯分布。此外,我们还利用伪标记目标样本来学习目标域中的域不变表示,进一步提高了迁移性能。大量的实验表明,我们提出的HoMM算法与现有的矩匹配算法相比有很大的优越性。
介绍
从矩匹配的角度来看,现有的基于离散点的UDA方法大多是基于最大平均差(MMD)或相关对齐(CORAL),用于不同分布的一阶(均值)和二阶(协方差)统计。然而,在实际应用中(如图像识别),深度特征往往是一个复杂的非高斯分布,不能完全用一阶或二阶统计量来表征,因此,利用这一方法只能保证分布的粗拟合。为了解决这一局限性,本文提出通过匹配高阶矩张量(主要是三阶和四阶矩张量)来进行域对齐,因为高阶矩张量包含更多的描述固有信息,能够更好地表示特征分布。图1展示了高阶矩张量的计算方法,其中绘制了一个由三个不同的高斯分布组成的点云和不同阶矩张量的水平集。正如所观察到的,高阶矩张量更准确地描述了分布。

图一 利用高阶矩张量进行域对齐的度量。正如所观察到的现象一样,使用高阶矩匹配能更准确地捕捉云团的形状。
本文的贡献包括以下两点:(1)提出了一种基于高阶矩匹配(HoMM)的域偏差最小化方法,期望该方法能够实现细粒度的域对齐。HoMM将MMD和CORAL集成为一个统一的框架,将一阶和二阶矩匹配推广为高阶矩张量匹配。在没有附加条件的情况下,三阶矩和四阶矩匹配比所有现有的基于离散的方法都要好得多。(2)针对目标域上缺乏标记的问题,提出了通过对可靠目标样本分配伪标记来学习目标域上的判别聚类方法,从而提高了迁移性能。
方法
在这项工作中,我们考虑的是一个无监督域自适应问题。源域是有监督数据,目标域是无监督数据,目标把源域上训练的分类器迁移到目标域上。 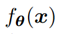 是深度神经网络的输出,并采用采用并流CNN结构进行无监督深度域自适应,如图二所示,源域与目标域的样本均共享相同的参数,并在最后一个全连接(FC)层进行域对齐。一个基本的域适应模型至少应该包括源域损失和域差异损失,其损失的基本表述为:
是深度神经网络的输出,并采用采用并流CNN结构进行无监督深度域自适应,如图二所示,源域与目标域的样本均共享相同的参数,并在最后一个全连接(FC)层进行域对齐。一个基本的域适应模型至少应该包括源域损失和域差异损失,其损失的基本表述为:

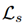 是源域的分类损失,
是源域的分类损失, 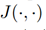 是交叉熵损失函数,
是交叉熵损失函数,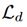 是域差异损失,如前所述,大多数存在的基于离散度的方法都是为了最小化二阶或更低的统计量。在这项工作中,提出了一种高阶矩匹配方法,它可以匹配不同域的高阶统计量。
是域差异损失,如前所述,大多数存在的基于离散度的方法都是为了最小化二阶或更低的统计量。在这项工作中,提出了一种高阶矩匹配方法,它可以匹配不同域的高阶统计量。
高阶矩匹配
为了执行细粒度的域对齐,我们将高阶矩匹配表示为

在训练过程中,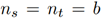
(b是每个batch的大小),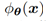 是适应层的激活输出。
是适应层的激活输出。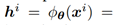
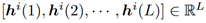 表征第i个样例的输出。L表示隐藏层的神经元个数。且
表征第i个样例的输出。L表示隐藏层的神经元个数。且

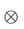 表示外积,而
表示外积,而

当p>3时,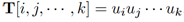 当p=1时,
当p=1时,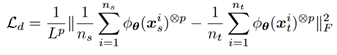 转化为
转化为 一阶矩匹配等价于线性矩阵矩阵不等式。
一阶矩匹配等价于线性矩阵矩阵不等式。
当p=2时,二阶HoMM表示为

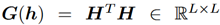
是一个Gram矩阵,因此,二阶HoMM相当于Gram矩阵的匹配。当激活输出减去平均值归一化后,集中的Gram矩阵就变成协方差矩阵。从这个角度看,二阶HoMM也相当于CORAL,它匹配域匹配的协方差矩阵。
除了一阶矩匹配(如MMD)和二阶模态匹配(如CORAL和Gram矩阵匹配),我们提出的HoMM还可以在p≥3时进行高阶模态张量匹配。由于高阶统计量可以更好地刻画非高斯分布,因此应用高阶矩匹配可以实现细粒度的域对齐。但是高阶模态张量匹配的复杂度太高,这使得高阶运动匹配在许多实际应用中不可行。为了解决这个问题,本文提出了两种实用的技术来进行高阶张量匹配。
组匹配
随着神经元数目的增加,空间复杂度呈指数增长,一种可行的方法是将适应层中隐藏的神经元分成 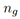 组,每一组为一个神经元群,其中神经元个数为
组,每一组为一个神经元群,其中神经元个数为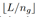 。然后分别计算并匹配各组的高阶张量。此时损失函数为:
。然后分别计算并匹配各组的高阶张量。此时损失函数为:

随机抽样匹配
当p=3/4时,组匹配可以凑效,但是p>5时,就会失去效果。因此,我们还提出了一种能够进行随机抽样匹配的策略。我们没有计算和匹配两个高维张量,而是随机选择高阶张量中的N个值,并且只计算和对齐源域和目标域中这N个值。此时的表达式是:

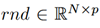 为随机产生的位置指数矩阵,因此,
为随机产生的位置指数矩阵,因此,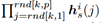 表征表示p级张量中的一个随机采样值
表征表示p级张量中的一个随机采样值 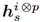 ,这样相当于在高维向量中,随机抽取N个值,并使这N个值一一对应
,这样相当于在高维向量中,随机抽取N个值,并使这N个值一一对应
希尔伯特空间里更高维特征匹配
此时
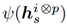 表示RKHS中的特征表示,根据所提出的随机抽样策略,域适应损失函数可以写成:
表示RKHS中的特征表示,根据所提出的随机抽样策略,域适应损失函数可以写成:

有区别聚类
当目标域特征与源域特征很好的匹配时,无监督域自适应问题就转化为半监督分类问题,已有大量工作尝试学习目标域中的判别聚类,其中大多数利用了熵正则化,以确保决策边界不跨越高密度数据区域

作者发现,当目标域具有较高的精度时,熵正则化的效果很好,但当测试精度不佳时,熵正则化的效果却很差,甚至降低了计算精度。其原因是由于熵的正则化使得某些误分类样本的概率过于自信,从而导致分类器被误导。本文提出了在共享特征空间中聚类的方法,而不是通过最小化条件熵的方法在输出层进行聚类。首先,选择目标域样例置信度比给定阈值高的样例,并给这些可靠的样本分配伪标签。然后,我们惩罚每个伪标记样本到其类中心的距离。判别聚类损失可表示为

由于我们是在小批量的基础上进行更新的,所以小样本无法准确地对中心进行定位。因此,我们在每次迭代中通过移动平均方法更新类中心。其表达式是:

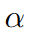 是学习率,
是学习率,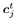 是第j类在第t次迭代的类中心,如果第i个样例属于第j类,
是第j类在第t次迭代的类中心,如果第i个样例属于第j类,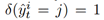 ,否则为0。
,否则为0。
损失函数
在此基础上,提出了一种融合(1)源域损耗最小化、(2)域对齐与高阶矩匹配和(3)目标域判别聚类的完备性方法,使无监督域自适应成为可能。完整的目标函数如下:

这篇关于HoMM: Higher-order Moment Matching for Unsupervised Domain Adaptation读书笔记的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




