用C++实现最小二乘法，最小区域法，最小包容圆拟合圆的算法和在Qt中的运行结果

本文主要是介绍用C++实现最小二乘法，最小区域法，最小包容圆拟合圆的算法和在Qt中的运行结果，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

用C++实现最小二乘法，最小区域法，最小包容圆拟合圆的算法和在Qt中的运行结果

我们工科生经常要处理数据，大家在处理数据的过程中遇到圆拟合的问题，一般会用到最小包容圆，最小外接圆，最小二乘拟合圆，最小区域法（遗传算法，粒子群算法），这里为了方便大家参考，提供C++实现最小二乘法，最小包容圆法，最小区域法（粒子群算法）的算法。话不多说，先上在Qt中的运行结果：

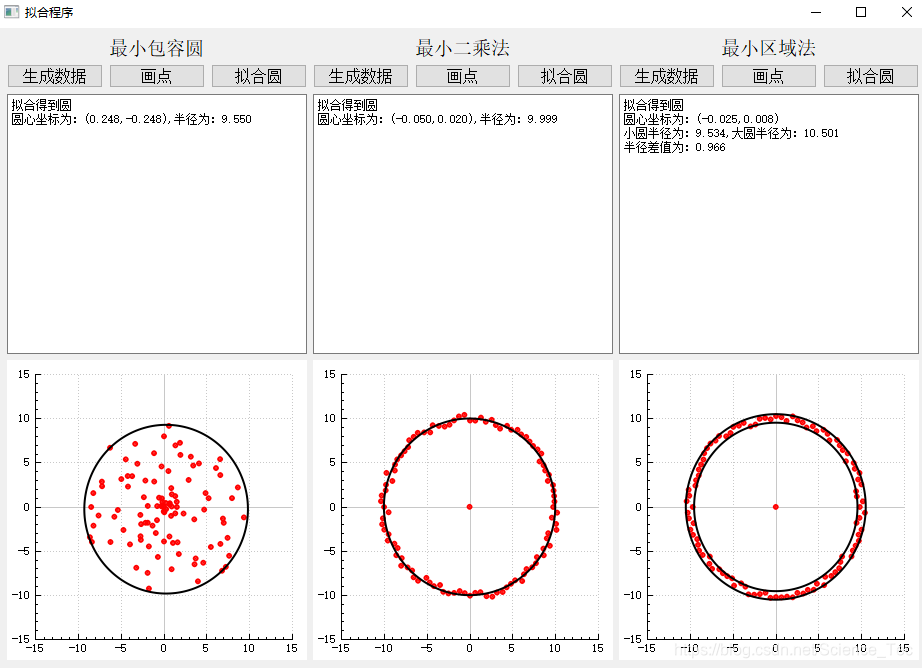
如图红色的点是随机生成的，图一中随机点在以原点为圆心，半径为10的圆内随机生成。其余两个图中点的范围在以原点为圆心，半径为9.5和10.5的同心圆范围内。黑色的线为拟合的圆。可以看到最小区域法的拟合比较精确。

下面附上三个算法代码的源文件和头文件（Qt中的代码，和C++稍微有一点不同，主要是为了可视化。大家可以根据需要自行修改。）

#ifndef LEASTSQUAREMETHODFITTINGCIRCLE_H
#define LEASTSQUAREMETHODFITTINGCIRCLE_H#include <QList>typedef struct pointInfo
{double x;double y;double radius;
}pointInfo;pointInfo LSFit(QList<pointInfo> &Point);   //最小二乘圆拟合函数#endif // LEASTSQUAREMETHODFITTINGCIRCLE_H

#include "leastsquaremethodfittingcircle.h"/* 最小二乘法圆拟合函数 */
pointInfo LSFit(QList<pointInfo> &Point)
{pointInfo tempPoint;        //定义临时变量，存储最小二乘圆心坐标double X1=0,Y1=0,X2=0,Y2=0,X3=0,Y3=0;double X1Y1=0,X1Y2=0,X2Y1=0;int N=Point.size();for(int i=0;i<Point.size();i++){double x=Point.at(i).x;double y=Point.at(i).y;double x2=x*x,y2=y*y;X1+=x;Y1+=y;X2+=x2;Y2+=y2;X3+=x*x2;Y3+=y*y2;X1Y1+=x*y;X1Y2+=x*y2;X2Y1+=x2*y;}double a=0,b=0,c=0;double C1=0,D1=0,E1=0,G1=0,H1=0;C1=N*X2-X1*X1;D1=N*X1Y1-X1*Y1;E1=N*X3+N*X1Y2-(X2+Y2)*X1;G1=N*Y2-Y1*Y1;H1=N*X2Y1+N*Y3-(X2+Y2)*Y1;a=(H1*D1-E1*G1)/(</