本文主要是介绍puzzle(0321)棋盘上的问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一,1*n的马的可达性
二,马的移动交换问题
1,Guarini谜题(对角马交换)
2,对边马交换
3,不规则棋盘的马交换
4,满盘马交换
三,其他问题
1,算法谜题 34 星星的硬币
2,算法谜题 14 复原国际象棋棋盘
一,1*n的马的可达性
象棋里面的马是1*2的马。
问题:1*n的马在一个无限大的棋盘上能否从一个指定的点跳到另一个指定的点?
如果n是奇数,那肯定是不能的。
把点哈希到整数,f=x+y,每次跳马都不会改变所到点的奇偶性,
所以奇偶性不同于起始点的所有点都是永远到不了的。
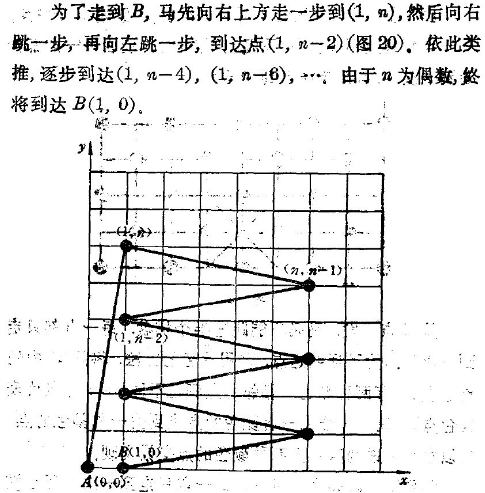
如果n是偶数,一定可以。
首先,“从一个指定的点跳到另一个指定的点”等价于“从一个点跳到与它相邻的点”
即从A(0,0)能不能跳到B(0,1)
二,马的移动交换问题
1,Guarini谜题(对角马交换)
通常认为本题在 1512 年出于 Paolo Guarini 之手, 但其实在公元 840 年左右就已经在阿拉伯棋谱中发现过它的踪迹了。
在 3*3 的国际象棋棋盘上有 4 枚骑士: 白方的两枚骑士位于底部两个角落, 黑方的两枚骑士位于顶部两个角落 (如图 1.6 所示)。试用最少的步骤移动棋子, 使得白方的骑士移至顶部两个角落, 而黑方的骑士移至底部两个角落。

由题意自然想到把棋盘的各个格子 (即在图 1.7 (a) 中简化成连续整数者) 表示成图的顶点, 这样就可以使用连接两个顶点的边来表示在顶点所代表的格子之间的一次移动。如果仿照棋盘上的原位来放置我们的顶点, 我们就会得到如图 1.7 (b) 所示的图(由于位于中央、编号为 5 的格子是骑士所走不到的位置, 因此这里就省略掉了) 。可是, 图 1.7 (b) 对问题求解没有多少助益。如果我们把顶点摆成一圈, 使得它们能够从顶点 1 开始依次被各枚骑士走到, 如图 1.7 (c) 所示, 这样就能够得到一张清楚得多的图案 。从图 1.7 (c) 中可以清楚地看出, 每一枚骑士走的每 一步都保留着所有的骑士之间按顺时针和逆时针排列的相对顺序。是故, 若要以最少步数解出这个谜题, 只有两种方法: 让每一枚骑士都按顺时针或逆时针方向沿着图示的边走, 直到每一枚骑士都首次抵达对角为止。而每个这样的对称解都需要总共16步。

题目没说要求白马和黑马不能互相攻击,不过显然是可以做到的。
这种神奇的解法当然也可以用在其他的地方,如 算法谜题34 星星的硬币
2,对边马交换
124象棋(14)
交换白马和黑马的位置,白马和黑马不能互相攻击
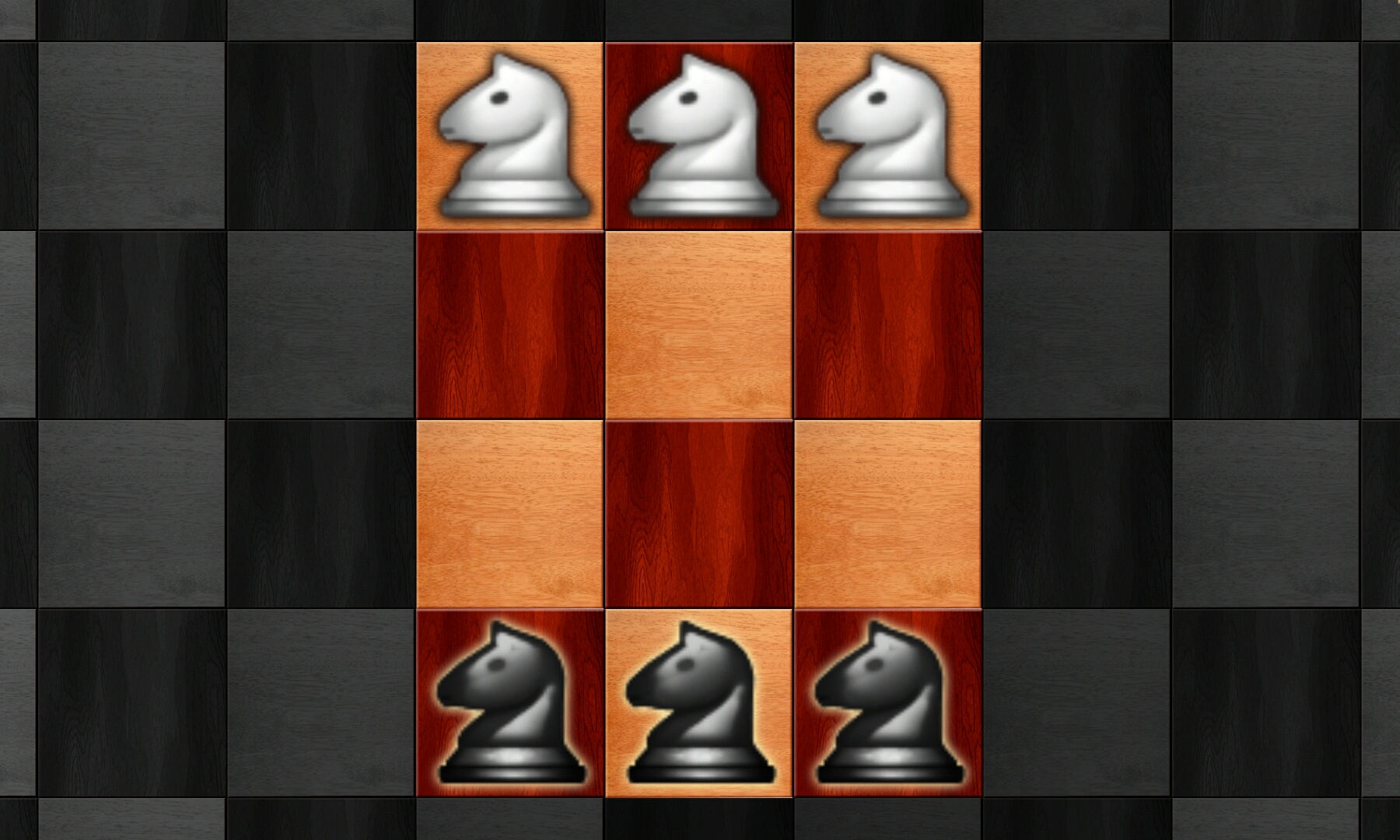
首先编号:
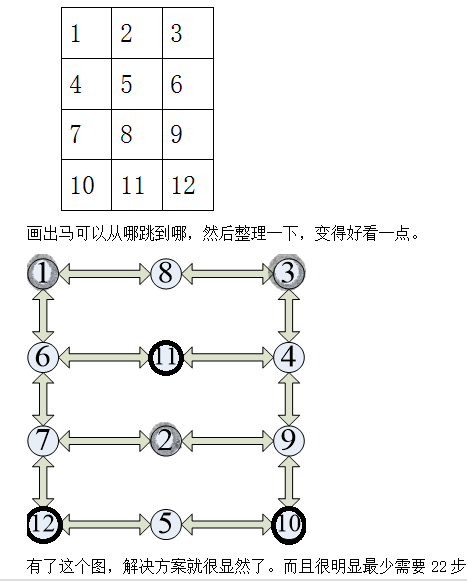
这样,就通过图的拓扑变换,将马在原图中的复杂的移动方式,化简成了在上图中的,特别简单的移动方式:每次只能上下或者左右移动一步,即沿着线路移动一步。
同时,白马和黑马的互斥,在上图中的映射为,白马和黑马相邻。
所以下面这个就是唯一最优解了,其他的最优解无非就是在上图中左右对称的另外一种,当然了,还有几步相邻的是独立的,顺序可以微调。

3,不规则棋盘的马交换
151象棋(9)
交换白马和黑马的位置

首先编号:
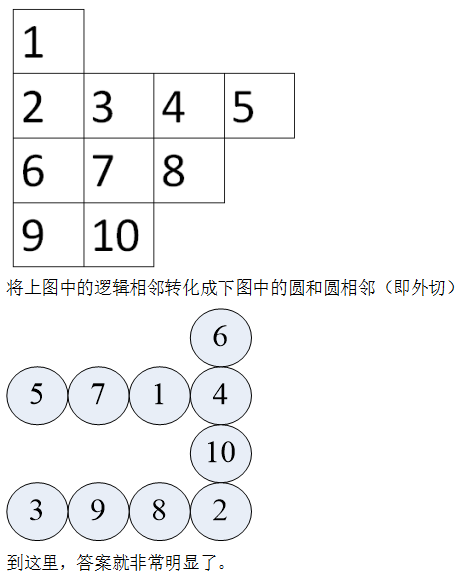
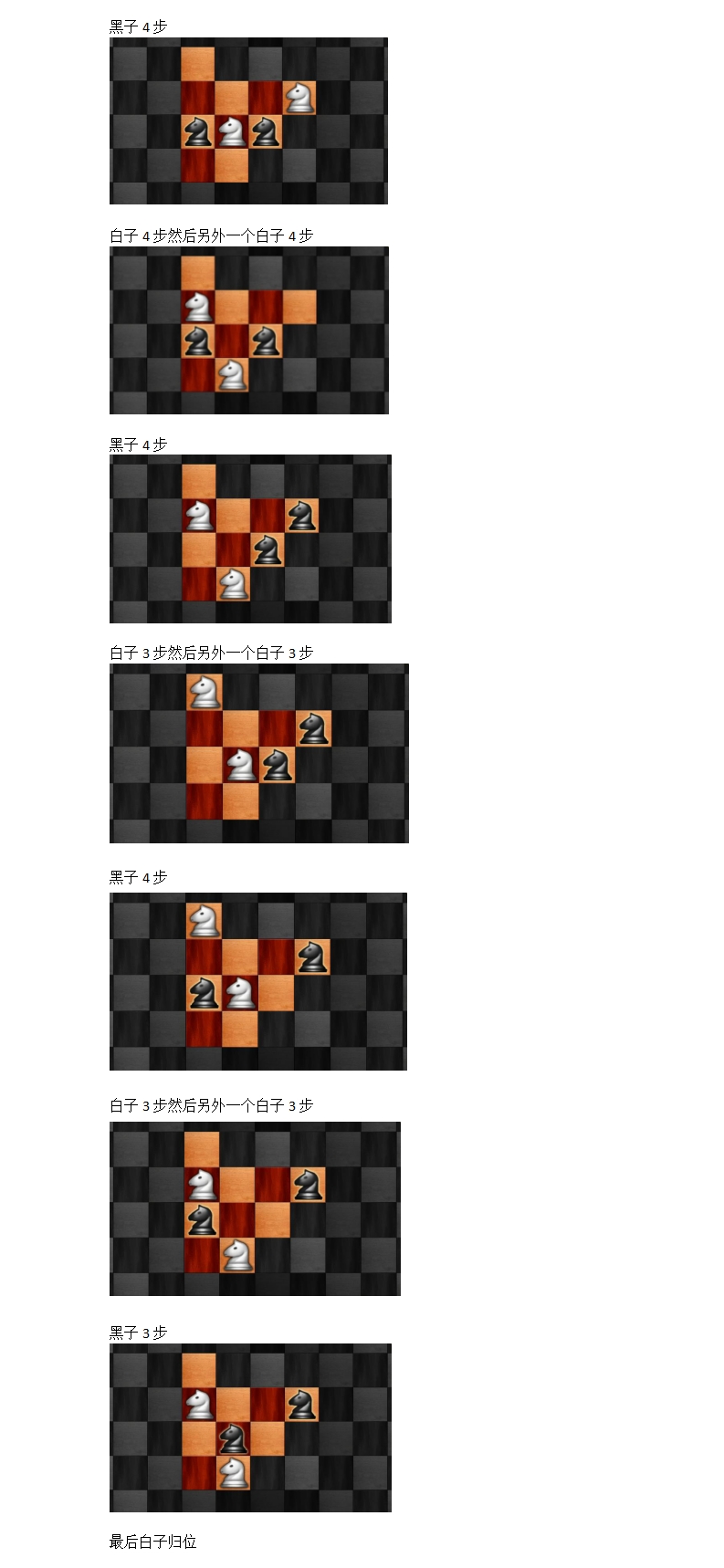
4,满盘马交换
28象棋(3)
交换白马和黑马的位置
游戏规则:
马走日,交换所有的白马和黑马即过关
在线puzzle:Toads And Frogs Puzzle in 2D
三,其他问题
1,算法谜题 34 星星的硬币
答案: 所能放置硬币的最大数是 7 。
我们将第一枚硬币放在顶点 6 上, 然后把它移动到顶点 1 , 记做 6->1,这将使得顶点 4 、 6 与顶点 1 相连的两条边不能再适用于另外一枚硬币的放置。
按照这种贪婪法的逻辑思路, 我们应该最小化这些不能使用的边的数目, 最大化仍然可以用于移动硬币的边的数目, 以此来放置硬币。这意味着第一枚硬币之后的每一枚硬币, 都应该沿着一条可用的边, 放置到拥有一条不能用的边的顶点上。 实现这一目的的最简便方法是让后一枚硬币停在前一枚硬币曾经放过的地方。例如, 7 枚硬币可以按照如下顺序放置:
6->1 3->6 8->3 5->8 2->5 7->2 4->7
很明显, 我们无法放置 8 枚硬币, 因为址 7 枚放好之后, 没有一个可以占用的顶点用于第 8 枚硬币的移动。


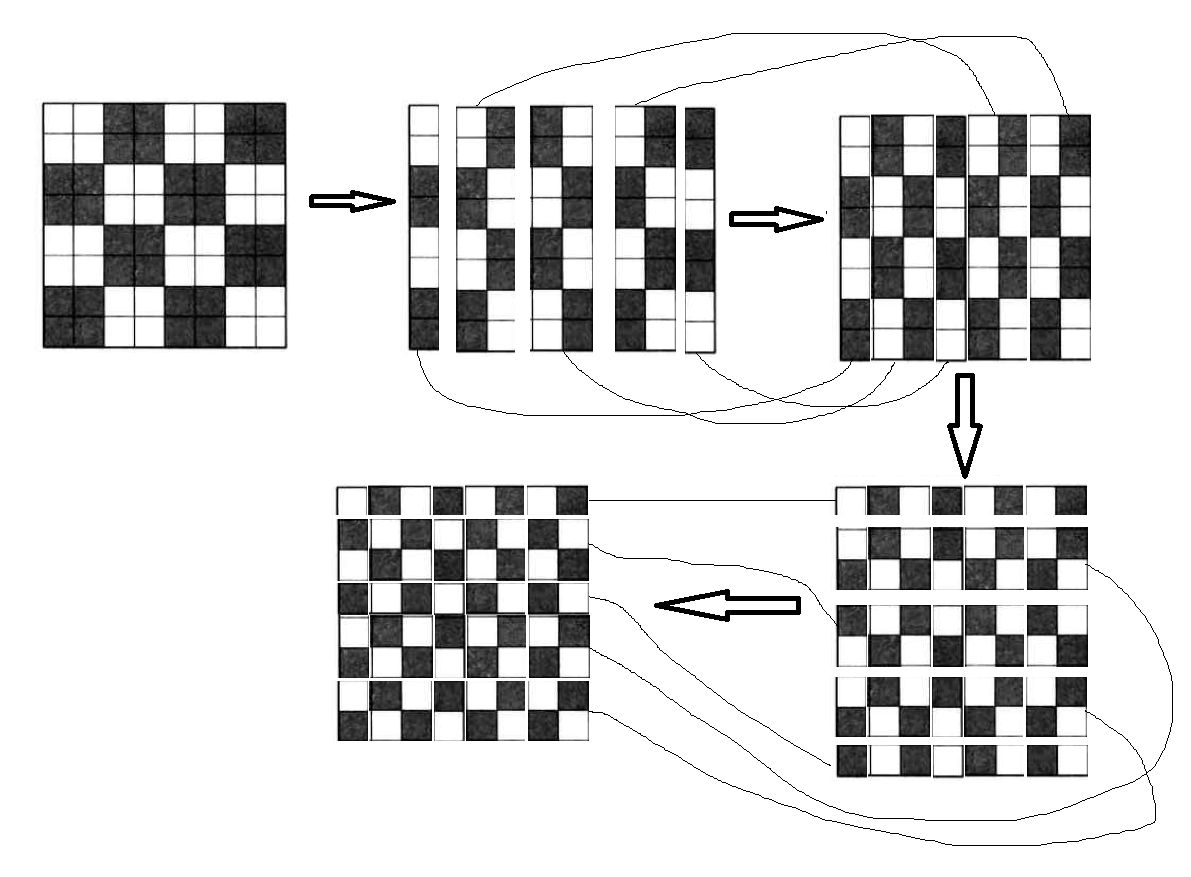
2,算法谜题 14 复原国际象棋棋盘
我的答案:
不难证明,上图中的8刀每一刀都是必不可少的,所以一共最少切分8次,而且切分8次只有如上一种切分方法能符合要求。
虽然切分方法只有一种,但是重组方法却有多种。
这篇关于puzzle(0321)棋盘上的问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!