本文主要是介绍计算几何之点操作【模板】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
点基本定义
与其说是点,不如说是一个二维向量类的定义,先给出类的完整定义,后文会一一详细介绍
class p {
public:ll x, y;//二维向量,表示一个点p(ll _x = 0, ll _y = 0):x(_x),y(_y){}//向量基本运算的实现+ - · *p operator+(const p& a)const { return p{ x + a.x,y + a.y }; }p operator-(const p& a)const { return p{ x - a.x,y - a.y }; }p operator-() const { return p{ -x,-y }; }ll operator|(const p& a)const { return x * a.x + y * a.y; }//点乘ll operator*(const p& a)const { return x * a.y - y * a.x; }//叉乘p operator*(const ll a)const { return p{ x * a,y * a }; }//向量数乘ll pow() const { return x * x + y * y; }//向量取平方//求距离double disPoint(const p& a) const;//点到点的距离double disline(const p& a, const p& b)const;//点到直线的距离double disSeg(const p& a, const p& b) const;//点到线段的距离};
double abs(const p& p) { return sqrt(p.pow()); }//向量取模
double triangle(p& a, p& b, p& c) { return (b - a) * (b - c) / 2.0; }//求三角形面积
利用向量求三角形面积
我们了解的三角形面积公式有
{ s = a h 2 s = a b sin θ 2 s = p ( p − a ) ( p − b ) ( p − c ) , ( p = a + b + c 2 ) \begin{cases} s=\frac{ah}{2} \\ s=\frac{ab\sin \theta }{2}\\ s=\sqrt[]{p(p-a)(p-b)(p-c)} ,(p=\frac{a+b+c}{2} ) \end{cases} ⎩ ⎨ ⎧s=2ahs=2absinθs=p(p−a)(p−b)(p−c),(p=2a+b+c)
而当给定三个顶点坐标 a = ( x 1 , y 1 ) , b = ( x 2 , y 2 ) , b = ( x 3 , y 3 ) a=(x_1,y_1),b=(x_2,y_2),b=(x_3,y_3) a=(x1,y1),b=(x2,y2),b=(x3,y3),求三角形面积,对计算机而言下面这个公式是最合适的:
s = ( x 2 − x 1 ) ( y 3 − y 1 ) − ( y 2 − y 1 ) ( x 3 − x 1 ) 2 s=\frac{(x_2-x_1)(y_3-y_1)-(y_2-y_1)(x_3-x_1)}{2} s=2(x2−x1)(y3−y1)−(y2−y1)(x3−x1)
众所周知,这个公式是由向量叉乘的来的,即我们求出向量 a b ⃗ , a c ⃗ \vec{ab},\vec{ac} ab,ac,二维向量叉乘的模的是以 a b , a c ab,ac ab,ac为两条边,所围成的平行四边形面积,我们求得 a b , a c ab,ac ab,ac,令其取二分之一即可得到上式
C o d e Code Code
double triangle(p& a, p& b, p& c) { return (b - a) * (b - c) / 2.0; }
判断点和线段的关系
首先我们可以讲点和线段的位置关系分为以下四种:

我们很容易发现当点在 3 , 4 3,4 3,4区域时,点和线段的夹角总是有一个钝角( ∠ p a b o r ∠ p b a \angle pab\space or \space \angle pba ∠pab or ∠pba),所以我们计算这对应向量的点积,就可以判断其余弦值的正负性,如果有小于 0 0 0的,那么点就在线段的这两个区域,根据 ∠ p a b \angle pab ∠pab和 ∠ p b a \angle pba ∠pba哪个是小于 0 0 0的,可以判断出点具体在哪个区域。
对于 1 , 2 1,2 1,2位置,我们求 a p ⃗ \vec{ap} ap和 a b ⃗ \vec{ab} ab的叉积,通过叉积的正负可以得到点的具体区域,如果叉积为 0 0 0,并且点不在 3 , 4 3,4 3,4区域,那么点就在选段上。
代码就是利用上文重载的运算符进行判断即可,这里就不给出代码了。
求点到线段的距离
我们判断点和线段的位置关系,是为了计算点到线段的距离,当点在 3 , 4 3,4 3,4区域时,点到线段的距离就是到其端点的距离,在 1 , 2 1,2 1,2区域时,点到线段的距离就是到对应直线的距离。前者的区里很好求,用点与点的距离公式计算即可。对于后者,我们利用公式:
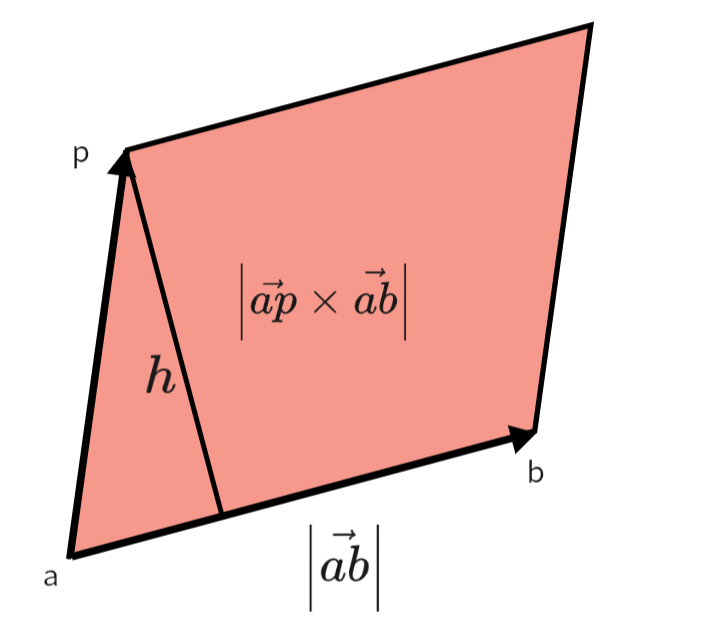
d = ∣ a p ⃗ × a b ⃗ ∣ ∣ a b ⃗ ∣ d=\frac{\left | \vec{ap}\times \vec{ab} \right | }{\left | \vec{ab}\right |} d= ab ap×ab
这个公式也非常容易推导,因为叉乘的模是对应向量所围成平行四边形的面积,而 ∣ a b ⃗ ∣ \left | \vec{ab} \right | ab 是底边长度,面积除以底就是高,就可以得到对应距离。
C o d e Code Code
double p::disPoint(const p& a) const {//点到点的距离return sqrt((x - a.x) * (x - a.x) + (y - a.y) * (y - a.y));
}
double p::disline(const p& a, const p& b)const {//点到直线的距离p ap = (*this) - a, ab = b - a;return abs(ap * ab) / abs(ab);
}
double p::disSeg(const p& a, const p& b)const {//点到线段的距离//判断点和线段的位置关系if (((sh - a) | (b - a)) <= 0 || ((sh - b) | (a - b)) <= 0)return min(sh.disPoint(a), sh.disPoint(b));return disline(a, b);
}
补题杭电5-A.Tyhoon
判断点是否在任意多边形内
作者太懒了,还没学……
射线法
角度和判断法
完整代码
#define eps 1e-8
class p {
public:double x, y;//二维向量,表示一个点p(double _x = 0, double _y = 0):x(_x),y(_y){}//向量基本运算的实现+ - · *p operator+(const p& a)const { return p{ x + a.x,y + a.y }; }p operator-(const p& a)const { return p{ x - a.x,y - a.y }; }p operator-() const { return p{ -x,-y }; }double operator|(const p& a)const { return x * a.x + y * a.y; }//点乘double operator*(const p& a)const { return x * a.y - y * a.x; }//叉乘p operator*(const ll a)const { return p{ x * a,y * a }; }//向量数乘double pow() const { return x * x + y * y; }//向量取平方//求距离double disPoint(const p& a) const;//点到点的距离double disline(const p& a, const p& b)const;//点到直线的距离double disSeg(const p& a, const p& b) const;//点到线段的距离};
double abs(const p& p) { return sqrt(p.pow()); }//向量取模double triangle(p& a, p& b, p& c) { return (b - a) * (b - c) / 2.0; }//求三角形面积double p::disPoint(const p& a) const {//点到点的距离return sqrt((x - a.x) * (x - a.x) + (y - a.y) * (y - a.y));
}double p::disline(const p& a, const p& b)const {//点到直线的距离p ap = (*this) - a, ab = b - a;return abs(ap * ab) / abs(ab);
}
double p::disSeg(const p& a, const p& b)const {//点到线段的距离//判断点和线段的位置关系if ((((*this) - a) | (b - a)) <= -eps || (((*this) - b) | (a - b)) <= -eps)return min(this->disPoint(a), this->disPoint(b));return disline(a, b);
}
这篇关于计算几何之点操作【模板】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



