图的最小生成树：Dijkstra迪杰斯特拉算法--源点到图中各节点的最短路径

图的最小生成树：Dijkstra迪杰斯特拉算法–源点到图中各节点的最短路径

提示：系列图的文章
提示：大厂笔试面试都可能不咋考的数据结构：图

由于图的结构比较难，出题的时候，很难把这个图的数据搞通顺，而且搞通顺了题目也需要耗费太多时间，故笔试面试都不会咋考
笔试大厂考的就是你的贪心取巧策略和编码能力，这完全不必用图来考你，其他的有大量的选择
面试大厂考你的是优化算法的能力，但是图没啥可以优化的，只要数据结构统一，它的算法是固定死的，所以不会在面试中考！
万一考，那可能都是大厂和图相关的业务太多，比如美团高德地图啥的，这种考的少。

但不管考不考，我们要有基础，要了解图的数据结构和算法。万一考了呢，准备以备不时之需。

图的数据结构比较难，算法是固定的套路
咱们需要统一一种自己熟悉的图的数据结构，方便套用算法时好写！！

下面是咱们得关于图的重要基础知识和重点应用：
（1）图数据结构，图的统一数据结构和非标准图的转化算法
（2）图的宽度优先遍历：BFS遍历
（3）图的深度优先遍历：DFS遍历

有了这些基础知识，咱就可以破解图的题目了
（4）图的拓扑排序：图的BFS的应用题
（5）图的最小生成树：Kruskal算法–并查集的经典应用，解决连通性问题
（6）图的最小生成树：Prim算法–解锁一批边，解锁一批节点

文章目录

• 图的最小生成树：Dijkstra迪杰斯特拉算法--源点到图中各节点的最短路径
• • @[TOC](文章目录)
• 生成树的定义
• 本题的图结构：Graph
• 什么是最小生成树？
• Dijkstra迪杰斯特拉算法：源点到图中各节点的最短路径
• 总结

生成树的定义

一个连通图的生成树是一个极小的连通子图，它包含图中全部的n个顶点，但只有构成一棵树的n-1条边。

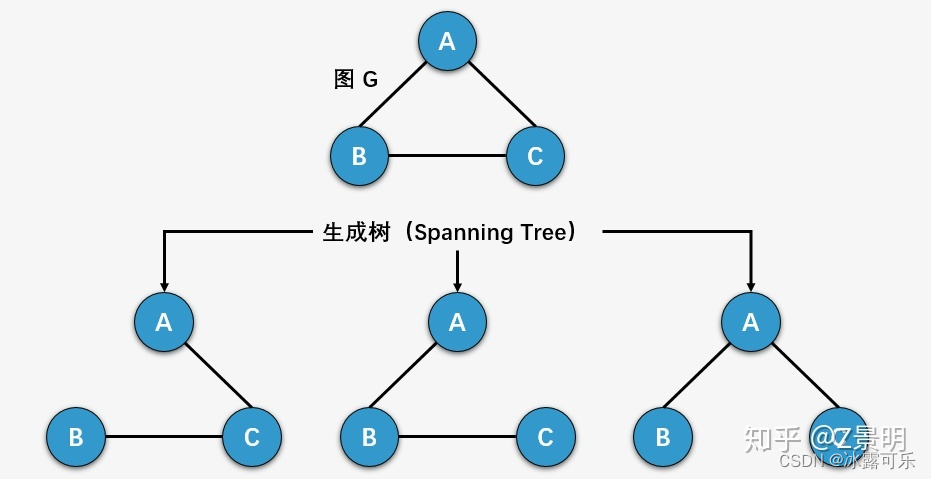
本题的图结构：Graph

就是统一的丰富图结构表示法：
这个文章必须看透：
这个文章必须看透：
这个文章必须看透：
（1）图数据结构，图的统一数据结构和非标准图的转化算法

//这里就不得不复习一下图的结构，左神标准的结构//边结构public static class Edge{public Node from;public Node to;//源节点和目的节点public int weight;//边的权public Edge(int w, Node f, Node t){weight = w;from = f;to = t;}}//点结构public static class Node{public int value;//值，这种图已经有了的，并查集就不不要包装了public int in;public int out;public ArrayList<Node> nexts;//直接邻居一堆动态数组节点public ArrayList<Edge> edges;//直接邻居的边，动态数组，一堆，个图一样public Node(int v){value = v;in = 0;out = 0;nexts = new ArrayList<>();edges = new ArrayList<>();}}//图结构public static class Graph{public HashMap<Integer, Node> nodes;//图的一堆节点，包出来了，并查集就不用包了public HashSet<Edge> edges;//图的一堆边public Graph(){nodes = new HashMap<>();edges = new HashSet<>();}}//建图的标准函数//这个主要是标准的左神图结构，这个玩意用来规整最明了简洁的图结构，方便实现很多图的算法public static Graph generateGraph(int[][] matrix){if (matrix == null || matrix.length == 0) return null;//无非就是构造一堆图节点，将节点们的参数初始化，边，边的参数初始化//一般图结构是二维数组：matrix,第一列是权，第二列：from节点，第三列：to节点//int[][] matrix = {//                {1,1,2},//                {2,2,3},//                {3,1,3}//        };Graph graph = new Graph();for (int i = 0; i < matrix.length; i++) {//每一行，读出来，构造节点int weight = matrix[i][0];int from = matrix[i][1];int to = matrix[i][2];//造节点,图中没有才造，否则不必---不然就要出问题，多造一些节点，导致混乱//****************这里出过大错！！！if (!graph.nodes.containsKey(from)) graph.nodes.put(from, new Node(from));if (!graph.nodes.containsKey(to)) graph.nodes.put(to, new Node(to));//获取节点Node fromNode = graph.nodes.get(from);Node toNode = graph.nodes.get(to);//造边Edge edge = new Edge(weight, fromNode, toNode);graph.edges.add(edge);toNode.in++;fromNode.out++;fromNode.nexts.add(toNode);fromNode.edges.add(edge);}//每一行都建好，返回图即可return graph;}//这些结构需要多写几遍，才能熟悉，记住，跟奥运健儿一样，多练习，才能稳定发挥

什么是最小生成树？

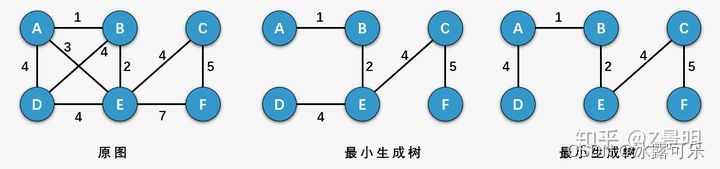
所谓一个 带权图 的最小生成树，就是原图中边的权值最小的生成树 ，
所谓最小是指边的权值之和小于或者等于其它生成树的边的权值之和。

Dijkstra迪杰斯特拉算法：源点到图中各节点的最短路径

指定一个点（源点）到其余各个顶点的最短路径，也叫做“单源最短路径”。
例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。

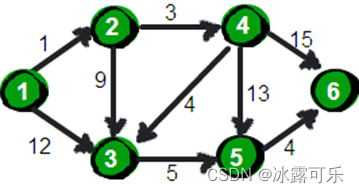
Dijkstra算法基于贪心思想，简单来讲就是两步：

（1）找出起点距离其他点的最短距离中的最小的那个
（2）用最小的来更新其他点的最短距离，更新完后舍弃

依我所见，迪杰斯特拉类似于排序，假设从起点到其他点的路径为边。
选出最短的边，通过最短的边来更新其他的边。
再通过第二短的边，更新其他的边。
整个过程就是从小到大依次找出从起点到其他点的最短边





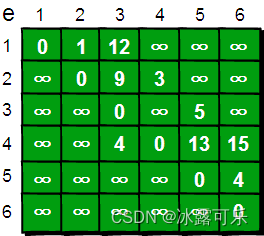
下面我们来模拟一下：

（1）最开始距离1最近的点是2节点，故1–2的距离直接敲定为1
（2）看看其他点，会不会因为这条边改变最短距离，因为最新这个短的距离，而更新其他节点–1的距离，这是可能的，需要就更新

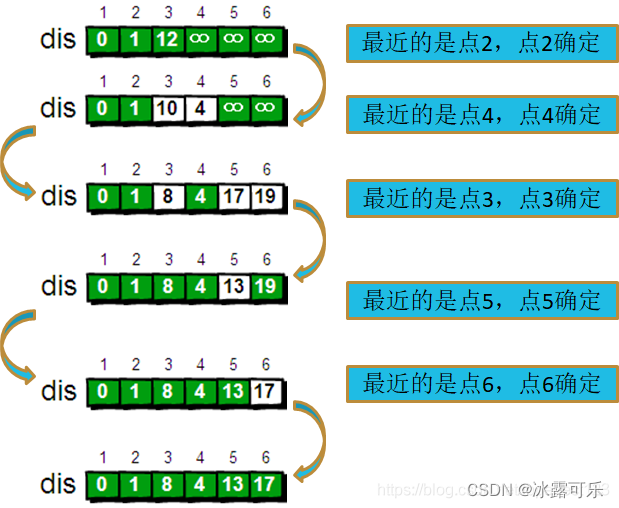
明白了就可以手撕代码了

public static Node getMinDistanceAndUnselectedNode(HashMap<Node, Integer> distanceMap,HashSet<Node> selectedNode){//当不做操作时，minNode是一个nullNode minNode = null;int min = Integer.MAX_VALUE;//无穷大//依次遍历距离表中的实体，而且要找没被用过的节点for(Map.Entry<Node, Integer> entry:distanceMap.entrySet()){Node node = entry.getKey();//拿节点int distance = entry.getValue();//拿距离if (!selectedNode.contains(node) && distance < min){//没用过的--且距离很短，直接赋给最小节点min = distance;minNode = node;}}return minNode;}//然后开始玩dijkstra算法public static HashMap<Node, Integer> dijkstraMST1(Node from){if (from == null) return null;HashMap<Node, Integer> distanceMap = new HashMap<>();HashSet<Node> selectedNode = new HashSet<>();distanceMap.put(from, 0);//起点Node minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNode);//先把起点找到while (minNode != null){//终止条件就是所有图中的点都被访问过了int distance = distanceMap.get(minNode);for (Edge edge:minNode.edges){Node toNode = edge.to;//拿到直接邻居if (!distanceMap.containsKey(toNode)){distanceMap.put(toNode, distance + edge.weight);//把最新的A--to节点的距离加上}else {//见过这个节点，更新--看看新距离是否更小distanceMap.put(toNode,Math.min(distance + edge.weight,distanceMap.get(toNode)));}}//所有邻居边都操作完后selectedNode.add(minNode);//记录最小生成树的那个点minNode = getMinDistanceAndUnselectedNode(distanceMap, selectedNode);//再去找现在最短距离的那个点}return distanceMap;}

测试一波：

public static void test(){int[][] matrix = {{1,1,2},{2,2,3},{3,3,4},{100,4,5},{5,2,5},{100,2,6},{7,5,6}};Graph graph = generateGraph(matrix);Node from = null;for (Node node:graph.nodes.values()){if (node.value == 1) from = node;break;//找到节点1}HashMap<Node, Integer> distanceMap = dijkstraMST1(from);for (Map.Entry<Node, Integer> entry:distanceMap.entrySet()){System.out.println(entry.getValue());}}public static void main(String[] args) {test();}

结果：

13
0
3
6
1
6

挺难的
但是思想要明白

总结

提示：重要经验：

1）图的算法是真的不困难，核心思想很简单，但是图的数据结构很难，在互联网大厂笔试面试中，没有任何人可以在笔试或者面试中写出来，时间太久了，这也不是考你撸代码的实力的好办法，更不是考你优化算法能力的最佳方案
2）dijkstra算法是不断用新的最短距离更新别的那些最短距离
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。