2019南京网络赛 B super_log —— 幂塔函数 广义欧拉降幂

本文主要是介绍2019南京网络赛 B super_log —— 幂塔函数 广义欧拉降幂，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接：点我啊╭(╯^╰)╮

题目大意：

    求 $a^{a^{..{.}^a}}mod$ $m$，共 $b$ 个 $a$

解题思路：

    

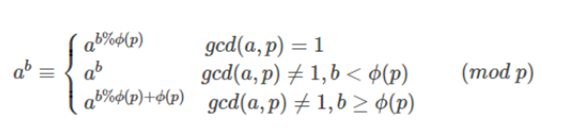
    注意对于指数取模的时候
    要判断计算指数会不会超过模数
    所以在快速幂里修改一下取模操作即可

    $PS：$ 对于 $gcd(a,p)=1$ 的情况可以直接套用广义定理

核心：欧拉降幂的运用

#include<bits/stdc++.h>
#define rint register int
#define deb(x) cerr<<#x<<" = "<<(x)<<'\n';
using namespace std;
typedef long long ll;
using pii = pair <ll, ll>;
const int maxn = 1e6 + 10;
int T;ll phi[maxn];
inline void phi_table(ll n) {	//计算1到n的欧拉函数值for(ll i = 2; i <= n; i++) phi[i] = 0;phi[1] = 1;for(ll i = 2; i <= n; i++) {if(!phi[i]) {for(ll j = i; j <= n; j+=i) {if(!phi[j]) phi[j] = j;phi[j] = phi[j] / i * (i - 1);}}}
}ll qpow(ll a, ll b, ll p) {ll ret = 1;while(b) {if(b & 1) ret = ret * a;ret = ret < p ? ret : (ret % p + p);a = a * a;a = a < p ? a : (a % p + p);b >>= 1;}return ret;
}ll dfs(ll k, ll m, ll a){if(m == 1) return 1;if(k == 0) return 1;ll exp = dfs(k-1, phi[m], a);return qpow(a, exp, m);
}int main() {ll a, b, m;scanf("%d", &T);phi_table(1e6 + 5);while(T--) {scanf("%lld%lld%lld", &a, &b, &m);if(m == 1) puts("0");else if(b == 0) puts("1");else if(b == 1) printf("%lld\n", a % m);else {ll ans = dfs(b, m, a);printf("%lld\n", ans % m);}}
}

这篇关于2019南京网络赛 B super_log —— 幂塔函数 广义欧拉降幂的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---