贪心算法正确性证明

贪心算法正确性证明

什么是贪心算法

WIKI定义：贪心算法（英语：greedy algorithm），又称贪婪算法，是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是最好或最优的算法。比如在旅行推销员问题中，如果旅行员每次都选择最近的城市，那这就是一种贪心算法。
用大白话说：我每一步都选择当下的最好选择，这样做下去我的最终结果就是最好的。
贪心算法是一种漂亮的算法设计思路，有很多应用，比如Prim算法。贪心算法在很多情况下可以得到最优解。（并不适用于所有情况，文章最后会给出反例）

贪心算法正确性证明
和这世界上大部分算法相同，贪心算法可以由数学归纳法证明其正确性。下面以Prim算法为例子给出证明过程：
对于一个给的的图G，其最小生成树集合为T*（一个图可以有多个最小生成树）,由算法求出的最小生成树为T，我们只需要在Prim算法的每一步得出的树T一直是T*的子集即可。

1.BaseCase: T是空树，因此T当然是T*的子集，BaseCase成立。

2.inductive: T是T的子集，下一步要将一条边e加到T中，求证T+e依旧是T的子集

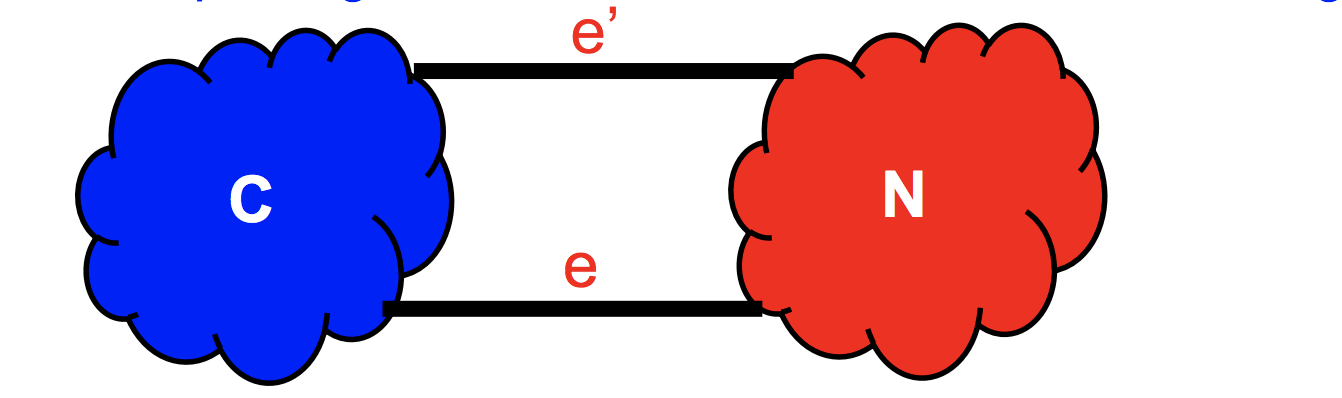
图中e’是属于T的一条边
第一种情况：e = e’,说明我们加入的边e是最小生成树中的一条边，T+e自然是T的子集，证明完毕。
第二种情况：e != e’，这时根据Prim算法规则（或者说根据贪心算法原理），e一定小于等于e’，即W(e) <= W(e’)，因此T+e’依旧是T*的一个子集，证明完毕。
有的读者可能会说这是Prim算法的证明过程，并不是贪心算法的证明。但是其实所有贪心算法都可以用这种方法证明，因为贪心算法的理念都是一样的，就是每一步时选择当下最优解可以得出最优结果，均可以由数学归纳法快速证明。
BTW:贪心算法天生就是为数学归纳法准备的，它自己的算法思想几乎就是证明过程。

反例：

我实在懒得打字+翻译成中文了，各位看官自行阅览吧，其实很容易就举出反例了