莫尔条纹--处理及分析 C++

老师评语：可以再利用骨架提取做一遍，两种方法比较精度，有需要的小伙伴可以直接参考！

1. 整体思路

通过观察原图像，图像存在噪声点，且黑色条纹边界不清晰，使用滤波、图像增强、二值化等方法对原图像进行预处理，另外为保证测量结果的准确性，使用图像三作为原图像，测量多个距离值并求均值。

 

原图像

中值滤波

图像增强（锐化）

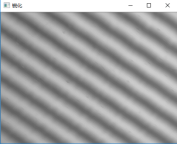
二值化

按位取反

膨胀：矩形结构元素、十字形结构元素，效果相差不大

腐蚀：矩形结构元素、十字形结构元素，十字形效果较好，选择十字形

轮廓检测及绘制

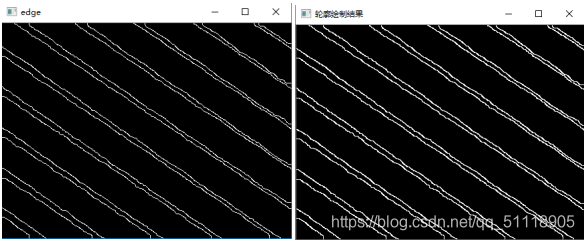
观察图像20个轮廓特征都为不规则曲线，利用霍夫直线检测无法准确检测出直线，由于图像由一个个图像点组成所以使用直线拟合的方法，将每个由像素点组成的轮廓拟合成直线。

获取轮廓像素坐标点

直线拟合

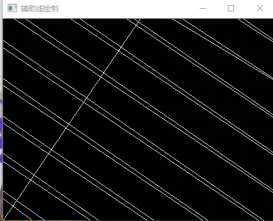
获取拟合直线斜率及解析式

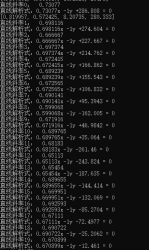
由于直线非平行直线无法直接求出图像之间的距离，求条纹间距时，两个阴影中心的距离=一个轮廓至下下轮廓的距离，使用等价代换的原则，计算直线1和直线3之间的距离。无法直接求解：方法1：两条直线，一条直线保持不变，另一条直线理解为一个个的点，求点到直线直接的距离再求均值

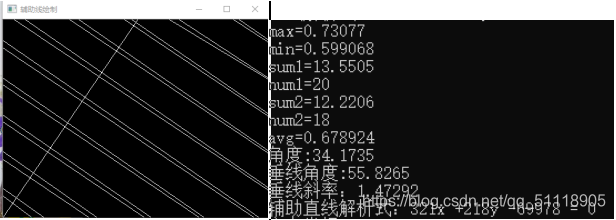
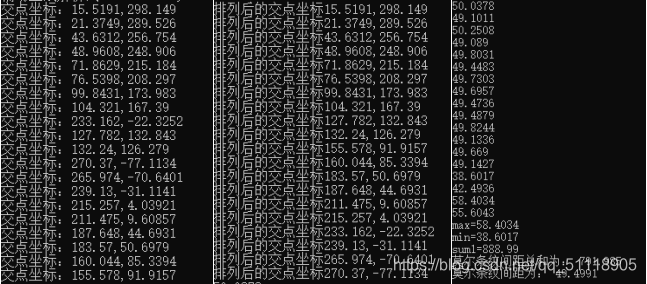
方法二：考虑到直线数量众多，方法一的计算量巨大，且受直线偏移影响严重。20条直线的斜率差别不大，求取20条直线的斜率，去掉最大值和最小值求均值，做出20条直线的类垂直线，求取他们之间的交点，获取交点坐标，利用公式计算交点1和交点3之间的距离，一共18个交点距离，去掉最大值和最小值求出均值，得出最终的距离49.4991个像素点。

2、程序源码

#include <iostream>

#include <opencv2/opencv.hpp>

using namespace std;

using namespace cv;

void drawLine(Mat &img, vector<Vec4i>lines, double rows, double cols, Scalar scalar, int n)

{

Point pt1, pt2;

for (size_t i = 0; i < lines.size();i++)

{

float rho = lines[i][0];

float theta = lines[i][1];

double a = cos(theta);

double b = sin(theta);

double x0 = a*rho, y0 = b*rho;

double length = max(rows, cols);

pt1.x = cvRound(x0 + length*(-b));

pt1.y = cvRound(y0 + length*(a));

pt2.x = cvRound(x0 - length*(-b));

pt2.y = cvRound(y0 - length*(a));

line(img, pt1, pt2, scalar, n);

}

}

int main() {

Mat image, gray, src, dst, gray1;//定义Mat类型的变量

image = imread("莫尔条纹3.png", 0);//读取程序文件夹中的图像，并赋值给变量image，0代表灰度图，1代表彩色图

if (!image.data) {

printf("could not find image");

return -1;

}

namedWindow("image", WINDOW_AUTOSIZE); //定义用户可调节大小的窗口，并命名为image

imshow("image", image);  //在image窗口里展示image图像

int w = image.cols;

int h = image.rows;

cout << "图像宽：" << w << endl;

cout << "图像高：" << h << endl;

//图像去噪(中值滤波)

medianBlur(image, src, 7);

imshow("meidan denoise demo", src);

//图像锐化

Mat kernel = (Mat_<char>(3, 3) << 0, -1, 0, -1, 5, -1, 0, -1, 0);

filter2D(src, dst, src.depth(), kernel);

imshow("锐化", dst);

//二值化

threshold(dst, gray, 120, 255, THRESH_BINARY );

imshow("gray", gray);

//按位取反

bitwise_not(gray, gray1);

imshow("gray1",gray1);

//形态学操作-膨胀

Mat struct1, struct2;

struct1 = getStructuringElement(0, Size(3, 3));  //矩形结构元素

struct2 = getStructuringElement(1, Size(3, 3));  //十字结构元素

Mat dilateGray, dilateGray1;

dilate(gray1, dilateGray, struct1, Point(-1, -1), 1);

dilate(gray1, dilateGray1, struct2, Point(-1, -1), 2);

imshow("dilateGray", dilateGray);

imshow("erodeGray1", dilateGray1);

//形态学操作-腐蚀

Mat erodeGray, erodeGray1;

Mat struct3, struct4;

struct3 = getStructuringElement(0, Size(3, 3));  //矩形结构元素

struct4 = getStructuringElement(1, Size(3, 3));  //十字结构元素

erode(dilateGray, erodeGray, struct3, Point(-1, -1), 3);

erode(dilateGray, erodeGray1, struct4, Point(-1, -1), 3);

imshow("erodeGray", erodeGray);

imshow("erodeGray1", erodeGray1);

Mat edge;

Canny(erodeGray, edge, 80, 180, 3, false);

//imshow("edge",edge);

//轮廓发现与绘制

vector<vector<Point>> contours;

vector<Vec4i> hierarchy;

Vec4f line0, line1, line2, line3, line4, line5, line6, line7, line8,line9,line10,line11,line12,line13,line14,line15, line16, line17, line18,line19;

findContours(edge, contours, hierarchy, RETR_TREE, CHAIN_APPROX_SIMPLE, Point());

//绘制轮廓

for (int t = 0; t < hierarchy.size(); t++)

{

drawContours(edge, contours, t, Scalar(255, 255, 255), 1, 4);

//printf("%d", t);

}

int m0, n0;

for (m0 = 0; m0 < contours.size(); m0++)

{

for (n0 = 0; n0 < contours[m0].size(); n0++)

cout << contours[m0][n0] << "";

cout << "\n";

}

//显示结果

imshow("轮廓绘制结果", edge);

vector<Point2f>point_0;

vector<Point2f>point_1;

vector<Point2f>point_2;

vector<Point2f>point_3;

vector<Point2f>point_4;

vector<Point2f>point_5;

vector<Point2f>point_6;

vector<Point2f>point_7;

vector<Point2f>point_8;

vector<Point2f>point_9;

vector<Point2f>point_10;

vector<Point2f>point_11;

vector<Point2f>point_12;

vector<Point2f>point_13;

vector<Point2f>point_14;

vector<Point2f>point_15;

vector<Point2f>point_16;

vector<Point2f>point_17;

vector<Point2f>point_18;

vector<Point2f>point_19;

int m, n;

for (m = 0; m < contours.size(); m++)

{

for (n = 0; n < contours[m].size(); n++)

{

switch (m)

{

case 0:

point_0.push_back(contours[m][n]);

break;

case 1:

point_1.push_back(contours[m][n]);

break;

case 2:

point_2.push_back(contours[m][n]);

break;

case 3:

point_3.push_back(contours[m][n]);

break;

case 4:

point_4.push_back(contours[m][n]);

break;

case 5:

point_5.push_back(contours[m][n]);

break;

case 6:

point_6.push_back(contours[m][n]);

break;

case 7:

point_7.push_back(contours[m][n]);

break;

case 8:

point_8.push_back(contours[m][n]);

break;

case 9:

point_9.push_back(contours[m][n]);

break;

case 10:

point_10.push_back(contours[m][n]);

break;

case 11:

point_11.push_back(contours[m][n]);

break;

case 12:

point_12.push_back(contours[m][n]);

break;

case 13:

point_13.push_back(contours[m][n]);

break;

case 14:

point_14.push_back(contours[m][n]);

break;

case 15:

point_15.push_back(contours[m][n]);

break;

case 16:

point_16.push_back(contours[m][n]);

break;

case 17:

point_17.push_back(contours[m][n]);

break;

case 18:

point_18.push_back(contours[m][n]);

break;

case 19:

point_19.push_back(contours[m][n]);

break;

default:

cout << "input error" << endl;

}

}

}

Mat img(321, 432,CV_8UC1, cv::Scalar(0));

//直线拟合0

fitLine(point_0, line0, DIST_L1, 0, 0.01, 0.01);

cout << line0 << endl;

double k0 = line0[1] / line0[0];

cout << "直线斜率0：  " << k0 << endl;

double A0 = k0, B0 = -1, C0 = line0[3] - k0*line0[2] ;

cout << "直线解析式：" << A0 << "x " << B0 << "y +" << C0 << " = 0 " << endl;

Point point00, point01;

point00.x = 0;

point00.y = C0;

point01.y = 321;

point01.x = (321-C0)/k0;

line(img, point00, point01, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合1

fitLine(point_1, line1, DIST_L1, 0, 0.01, 0.01);

cout << line1 << endl;

double k1 = line1[1] / line1[0];

cout << "直线斜率1：  " << k1 << endl;

double A1 = k1, B1 = -1, C1 = line1[3] - k1*line1[2] ;

cout << "直线解析式：" << A1 << "x " << B1 << "y +" << C1 << " = 0 " << endl;

Point point10, point11;

point10.x = 0;

point10.y = C1;

point11.y = 321;

point11.x = (321 - C1) / k1;

line(img, point10, point11, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合2

fitLine(point_2, line2, DIST_L1, 0, 0.01, 0.01);

double k2 = line2[1] / line2[0];

cout << "直线斜率2：  " << k2 << endl;

double A2 = k2, B2 = -1, C2 = line2[3] - line2[2] * k2;

cout << "直线解析式：" << A2 << "x " << B2 << "y +" << C2 << " = 0 " << endl;

Point point20, point21;

point20.x = 0;

point20.y = C2;

point21.y = 321;

point21.x = (321 - C2) / k2;

line(img, point20, point21, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合3

fitLine(point_3, line3, DIST_L1, 0, 0.01, 0.01);

double k3 = line3[1] / line3[0];

cout << "直线斜率3：  " << k3 << endl;

double A3 = k3, B3 = -1, C3 = line3[3] - line3[2] * k3;

cout << "直线解析式：" << A3 << "x " << B3 << "y +" << C3 << " = 0 " << endl;

Point point30, point31;

point30.x = 0;

point30.y = C3;

point31.y = 321;

point31.x = (321 - C3) / k3;

line(img, point30, point31, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合4

fitLine(point_4, line4, DIST_L1, 0, 0.01, 0.01);

double k4 = line4[1] / line4[0];

cout << "直线斜率4：  " << k4 << endl;

double A4 = k4, B4 = -1, C4 =  line4[3] - line4[2] * k4;

cout << "直线解析式：" << A4 << "x " << B4 << "y +" << C4 << " = 0 " << endl;

Point point40, point41;

point40.x = 0;

point40.y = C4;

point41.y = 321;

point41.x = (321 - C4) / k4;

line(img, point40, point41, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合5

fitLine(point_5, line5, DIST_L1, 0, 0.01, 0.01);

double k5 = line5[1] / line5[0];

cout << "直线斜率5：  " << k5 << endl;

double A5 = k5, B5 = -1, C5 = line5[3] - line5[2] * k5;

cout << "直线解析式：" << A5 << "x " << B5 << "y +" << C5 << " = 0 " << endl;

Point point50, point51;

point50.x = 0;

point50.y = C5;

point51.y = 321;

point51.x = (321 - C5) / k5;

line(img, point50, point51, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合6

fitLine(point_6, line6, DIST_L1, 0, 0.01, 0.01);

double k6 = line6[1] / line6[0];

cout << "直线斜率6：  " << k6 << endl;

double A6 = k6, B6 = -1, C6 = line6[3] - line6[2] * k6;

cout << "直线解析式：" << A6 << "x " << B6 << "y +" << C6 << " = 0 " << endl;

Point point60, point61;

point60.x = 0;

point60.y = C6;

point61.y = 321;

point61.x = (321 - C6) / k6;

line(img, point60, point61, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合7

fitLine(point_7, line7, DIST_L1, 0, 0.01, 0.01);

double k7 = line7[1] / line7[0];

cout << "直线斜率7：  " << k7 << endl;

double A7 = k7, B7 = -1, C7 = line7[3] - line7[2] * k7;

cout << "直线解析式：" << A7 << "x " << B7 << "y +" << C7 << " = 0 " << endl;

Point point70, point71;

point70.x = 0;

point70.y = C7;

point71.y = 321;

point71.x = (321 - C7) / k7;

line(img, point70, point71, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合8

fitLine(point_8, line8, DIST_L1, 0, 0.01, 0.01);

double k8 = line8[1] / line8[0];

cout << "直线斜率8：  " << k8 << endl;

double A8 = k8, B8 = -1, C8 = line8[3] - line8[2] * k8;

cout << "直线解析式：" << A8 << "x " << B8 << "y " << C8 << " = 0 " << endl;

Point point80, point81;

point80.x = 0;

point80.y = C8;

point81.y = 321;

point81.x = (321 - C8) / k8;

line(img, point80, point81, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合9

fitLine(point_9, line9, DIST_L1, 0, 0.01, 0.01);

double k9 = line9[1] / line9[0];

cout << "直线斜率9：  " << k9 << endl;

double A9 = k9, B9 = -1, C9 = line9[3] - line9[2] * k9;

cout << "直线解析式：" << A9 << "x " << B9 << "y +" << C9 << " = 0 " << endl;

Point point90, point91;

point90.x = 0;

point90.y = C9;

point91.y = 321;

point91.x = (321 - C9) / k9;

line(img, point90, point91, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合10

fitLine(point_10, line10, DIST_L1, 0, 0.01, 0.01);

double k10 = line10[1] / line10[0];

cout << "直线斜率10：  " << k10 << endl;

double A10 = k10, B10 = -1, C10 =  line10[3] - line10[2] * k10;

cout << "直线解析式：" << A10 << "x " << B10 << "y +"<< C10 << " = 0 " << endl;

Point point100, point101;

point100.x = -C10/A10;

point100.y = 0;

point101.x = 432;

point101.y = A10 * 432 + C10;

line(img, point100, point101, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合11

fitLine(point_11, line11, DIST_L1, 0, 0.01, 0.01);

double k11 = line11[1] / line11[0];

cout << "直线斜率11：  " << k11 << endl;

double A11 = k11, B11 = -1, C11 = line11[3] - line11[2] * k11;

cout << "直线解析式：" << A11 << "x " << B11 << "y " << C11 << " = 0 " << endl;

Point point110, point111;

point110.x = -C11 / A11;

point110.y = 0;

point111.x = 432;

point111.y = A11 * 432 + C11;

line(img, point110, point111, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合12

fitLine(point_12, line12, DIST_L1, 0, 0.01, 0.01);

double k12 = line12[1] / line12[0];

cout << "直线斜率12：  " << k12 << endl;

double A12 = k12, B12 = -1, C12 = line12[3] - line12[2] * k12;

cout << "直线解析式：" << A12 << "x " << B12 << "y " << C12 << " = 0 " << endl;

Point point120, point121;

point120.x = -C12 / A12;

point120.y = 0;

point121.x = 432;

point121.y = A12 * 432 + C12;

line(img, point120, point121, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合13

fitLine(point_13, line13, DIST_L1, 0, 0.01, 0.01);

double k13 = line13[1] / line13[0];

cout << "直线斜率13：  " << k13 << endl;

double A13 = k13, B13 = -1, C13 = line13[3] - line13[2] * k13;

cout << "直线解析式：" << A13 << "x " << B13 << "y " << C13 << " = 0 " << endl;

Point point130, point131;

point130.x = -C13 / A13;

point130.y = 0;

point131.x = 432;

point131.y = A13 * 432 + C13;

line(img, point130, point131, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合14

fitLine(point_14, line14, DIST_L1, 0, 0.01, 0.01);

double k14 = line14[1] / line14[0];

cout << "直线斜率14：  " << k14 << endl;

double A14 = k14, B14 = -1, C14 = line14[3] - line14[2] * k14;

cout << "直线解析式：" << A14 << "x " << B14 << "y " << C14 << " = 0 " << endl;

Point point140, point141;

point140.x = -C14 / A14;

point140.y = 0;

point141.x = 432;

point141.y = A14 * 432 + C14;

line(img, point140, point141, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合15

fitLine(point_15, line15, DIST_L1, 0, 0.01, 0.01);

double k15 = line15[1] / line15[0];

cout << "直线斜率15：  " << k15 << endl;

double A15 = k15, B15 = -1, C15 = line15[3] - line15[2] * k15;

cout << "直线解析式：" << A15 << "x " << B15 << "y " << C15 << " = 0 " << endl;

Point point150, point151;

point150.x = -C15 / A15;

point150.y = 0;

point151.x = 432;

point151.y = A15 * 432 + C15;

line(img, point150, point151, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合16

fitLine(point_16, line16, DIST_L1, 0, 0.01, 0.01);

double k16 = line16[1] / line16[0];

cout << "直线斜率16：  " << k16 << endl;

double A16 = k16, B16 = -1, C16 = line16[3] - line16[2] * k16;

cout << "直线解析式：" << A16 << "x " << B16 << "y " << C16 << " = 0 " << endl;

Point point160, point161;

point160.x = -C16 / A16;

point160.y = 0;

point161.x = 432;

point161.y = A16 * 432 + C16;

line(img, point160, point161, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合17

fitLine(point_17, line17, DIST_L1, 0, 0.01, 0.01);

double k17 = line17[1] / line17[0];

cout << "直线斜率17：  " << k17 << endl;

double A17 = k17, B17 = -1, C17 = line17[3] - line17[2] * k17;

cout << "直线解析式：" << A17 << "x " << B17 << "y " << C17 << " = 0 " << endl;

Point point170, point171;

point170.x = -C17 / A17;

point170.y = 0;

point171.x = 432;

point171.y = A17 * 432 + C17;

line(img, point170, point171, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合18

fitLine(point_18, line18, DIST_L1, 0, 0.01, 0.01);

double k18 = line18[1] / line18[0];

cout << "直线斜率18：  " << k18 << endl;

double A18 = k18, B18 = -1, C18 = line18[3] - line18[2] * k18;

cout << "直线解析式：" << A18 << "x " << B18 << "y " << C18 << " = 0 " << endl;

Point point180, point181;

point180.x = -C18 / A18;

point180.y = 0;

point181.x = 432;

point181.y = A18 * 432 + C18;

line(img, point180, point181, Scalar(255, 255, 255), 1, LINE_8, 0);

//直线拟合19

fitLine(point_19, line19, DIST_L1, 0, 0.01, 0.01);

double k19 = line19[1] / line19[0];

cout << "直线斜率19：  " << k19 << endl;

double A19 = k19, B19 = -1, C19 = line19[3] - line19[2] * k19;

cout << "直线解析式：" << A19 << "x " << B19 << "y " << C19 << " = 0 " << endl;

Point point190, point191;

point190.x = -C19 / A19;

point190.y = 0;

point191.x = 432;

point191.y = A19 * 432 + C19;

line(img, point190, point191, Scalar(255, 255, 255), 1, LINE_8, 0);

//舍弃最大值及最小值，求斜率均值

double a[20] = { k0,k1,k2,k3,k4,k5,k6,k7,k8,k9,k10,k11,k12,k13,k14,k15,k16,k17,k18,k19 };

double sum = 0;

int num = 20;

//for 循环判断最大值和最小值

double max = a[0];

double min = a[0];

for (int i = 0; i < 20; i++)

{

if (a[i] > max)

max = a[i];

if (a[i] < min)

min = a[i];

sum += a[i];

}

cout << "max=" << max << endl;

cout << "min=" << min << endl;

cout << "sum1=" << sum << endl;

cout << "num1=" << num << endl;

//for循环去除最大值和最小值

for (int i = 0; i < 20; i++)

{

if (a[i] == max || a[i] == min)

{

sum -= a[i];

num--;

}

}

cout << "sum2=" << sum << endl;

cout << "num2=" << num << endl;

double avg = sum / num;

cout << "avg=" << avg << endl;

double b = atan(avg);            //弧度制

double c = b * 180 / 3.1415926;  //角度制

cout << "角度:" << c << endl;

double d = 90 - c;

cout << "垂线角度:" << d << endl;

double e = tan(d*3.1415926/180);

cout << "垂线斜率：" << e << endl;

//辅助线的一般直线公式

double AA = 321, BB = 218, CC = -321 * 218;

cout << "辅助直线解析式：" << AA<< "x +" << BB << "y " << CC << " = 0 " << endl;

//直线绘制

line(img,Point(0,321), Point(218,0),Scalar(255,255,255),1,LINE_8,0);

imshow("辅助线绘制", img);

//求取直线交点

double A[20] = { A0,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A14,A15,A16,A17,A18,A19 };

double B[20] = { B0,B1,B2,B3,B4,B5,B6,B7,B8,B9,B10,B11,B12,B13,B14,B15,B16,B17,B18,B19 };

double C[20] = { C0,C1,C2,C3,C4,C5,C6,C7,C8,C9,C10,C11,C12,C13,C14,C15,C16,C17,C18,C19 };

double D[20], x[20], y[20];

for (int i = 0; i < 20; i++)

{

D[i] = A[i] * BB - AA * B[i];

x[i] = (B[i] * CC - BB * C[i]) / D[i];

y[i] = (AA * C[i] - A[i] * CC) / D[i];

cout << "交点坐标：" << x[i] << "," << y[i] << endl;

}

//x从小到大排列数组

double tempx;

double tempy;

for (int i = 1; i < 20; i++)

{

for (int j = i - 1; j >= 0; j--)

{

if (x[j + 1] < x[j])

{

tempx = x[j];

x[j] = x[j + 1];

x[j + 1] = tempx;

}

else break;

}

}

for (int i = 0; i < 20; i++)

{

cout << x[i] << endl;

}

//y从大到小排列数组

for (int i = 1; i < 20; i++)

{

for (int j = i - 1; j >= 0; j--)

{

if (y[j + 1] > y[j])

{

tempy = y[j];

y[j] = y[j + 1];

y[j + 1] = tempy;

}

else break;

}

}

for (int i = 0; i < 20; i++)

{

cout <<"排列后的交点坐标"<<x[i]<<","<< y[i] << endl;

}

//计算距离

double dis[18];

for (int i = 0; i < 18; i++)

{

int j = i + 2;

dis[i] = sqrt(pow((x[j] - x[i]),2) + pow((y[j] - y[i]),2));//pow平方,sqrt开平方

}

for (int i = 0; i < 18; i++)

{

cout << dis[i] << endl;

}

//去掉距离最大值、最小值，求平均

double sum_dis = 0;

//for 循环判断最大值和最小值

double max_dis = dis[0];

double min_dis = dis[0];

for (int i = 0; i < 18; i++)

{

if (dis[i] > max_dis)

max_dis = dis[i];

if (dis[i] < min_dis)

min_dis = dis[i];

sum_dis += dis[i];

}

cout << "max=" << max_dis << endl;

cout << "min=" << min_dis << endl;

cout << "sum1=" << sum_dis << endl;

//for循环去除最大值和最小值

for (int i = 0; i < 18; i++)

{

if (dis[i] == max_dis || dis[i] == min_dis)

{

sum_dis -= dis[i];

}

}

double avg_dis = sum_dis / 16;

cout << "莫尔条纹间距总和为： " << sum_dis << endl;

cout << "莫尔条纹间距为： " << avg_dis << endl;

/*//霍夫直线检测

vector<Vec4i> lines1, lines2;

HoughLinesP(edge, lines1, 5, CV_PI / 180.0, 150, 100, 1000);

HoughLinesP(edge, lines2, 5, CV_PI / 180.0, 150, 30, 30);

Mat img1, img2;

edge.copyTo(img1);

edge.copyTo(img2);

drawLine(img1, lines1, edge.rows, edge.cols, Scalar(255), 1);

drawLine(img2, lines2, edge.rows, edge.cols, Scalar(255), 1);

imshow("img1", img1);

imshow("img2", img2);*/

waitKey(0);

return 0;

}