绝缘检测原理和绝缘电阻计算方法

本文主要是介绍绝缘检测原理和绝缘电阻计算方法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

简介
绝缘检测功能
绝缘检测原理
绝缘电阻检测的常用方法
- 不平衡电桥法
绝缘电阻
- 绝缘电阻的计算
绝缘检测开启或关闭
为什么根据 V1 ＜ V2 或 V1 ≥ V2 判断是上桥臂并入电阻还是下桥臂并入电阻

简介

绝缘检测是判断动力（正、负）总线与外壳“地”是否存在连接

一些意外情况会发生绝缘故障，比如高压插件老化、积灰、进水、动力走线不合理因（车辆运行）震动摩擦发生破皮

绝缘故障其实就是“电阻”从动力线回路异常“搭”到了不该“搭”到的地方（比如PACK包、车架）

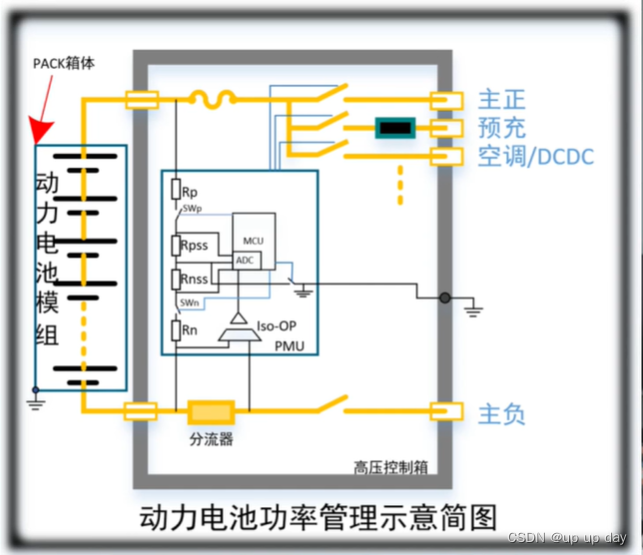
在这里插入图片描述

绝缘检测功能

简单来说，绝缘检测就是检测电池包是否漏电

绝缘检测原理

理想状态下，电池包的高压+ 和高压- 对车身地的绝缘阻值应该 ∞

Rn、Rp只要有一方阻值足够大，车身地与电池不形成导电回路，那么它们之间就是绝缘的。只有当Rn、Rp绝缘阻值同时降到一定值，高压电池回路对车身地形成漏电回路，才会造成短路的情况。
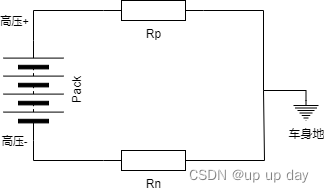
在这里插入图片描述

绝缘电阻检测的常用方法

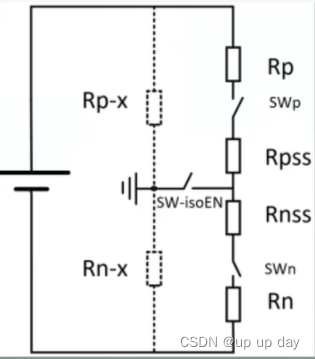
不平衡电桥法

在每一侧增加了一路开关和一个电阻，通过交替切换两侧的开关改变两极对地的等效电阻，得到正、负极检测电阻上不平衡的检测电压，从而计算出正负极的绝缘电阻，正负极检测电阻上的电压随着开关切换周期变化，当某一极绝缘电阻变低时该侧检测电阻电压变小，对应另一侧检测电阻的电压变大。

优点是能准确的检测正负极的绝缘电阻，缺点是切换开关后电路需要等待一段时间达到稳态，相对来说检测时间长。

绝缘电阻

绝缘检测的目的就是计算绝缘电阻，当绝缘电阻低于某个阈值，则很可能会造成电池短路、漏电，威胁人员安全

Rp 和 Rn 在数学上就是两个未知数
求绝缘电阻就是去求解这两个未知数
因此问题就变成了用电路知识去构建包含Rp 和Rn 的二元一次方程

在这里插入图片描述

绝缘电阻的计算

以下面绝缘检测方案为例：

绝缘检测前：K1 K2 K3 全部断开

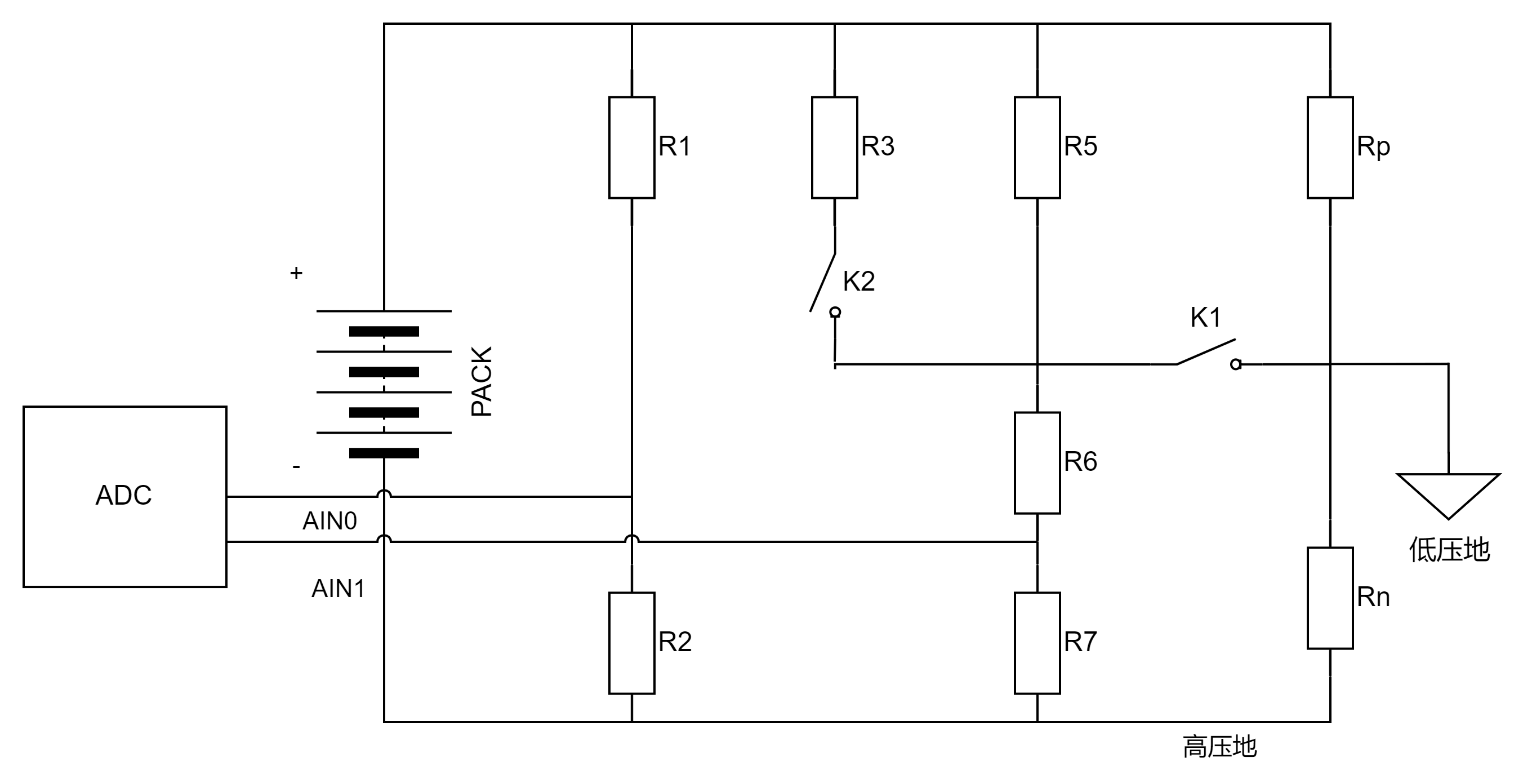
步骤一：闭合 K1，开始绝缘检测，整体电路如下所示
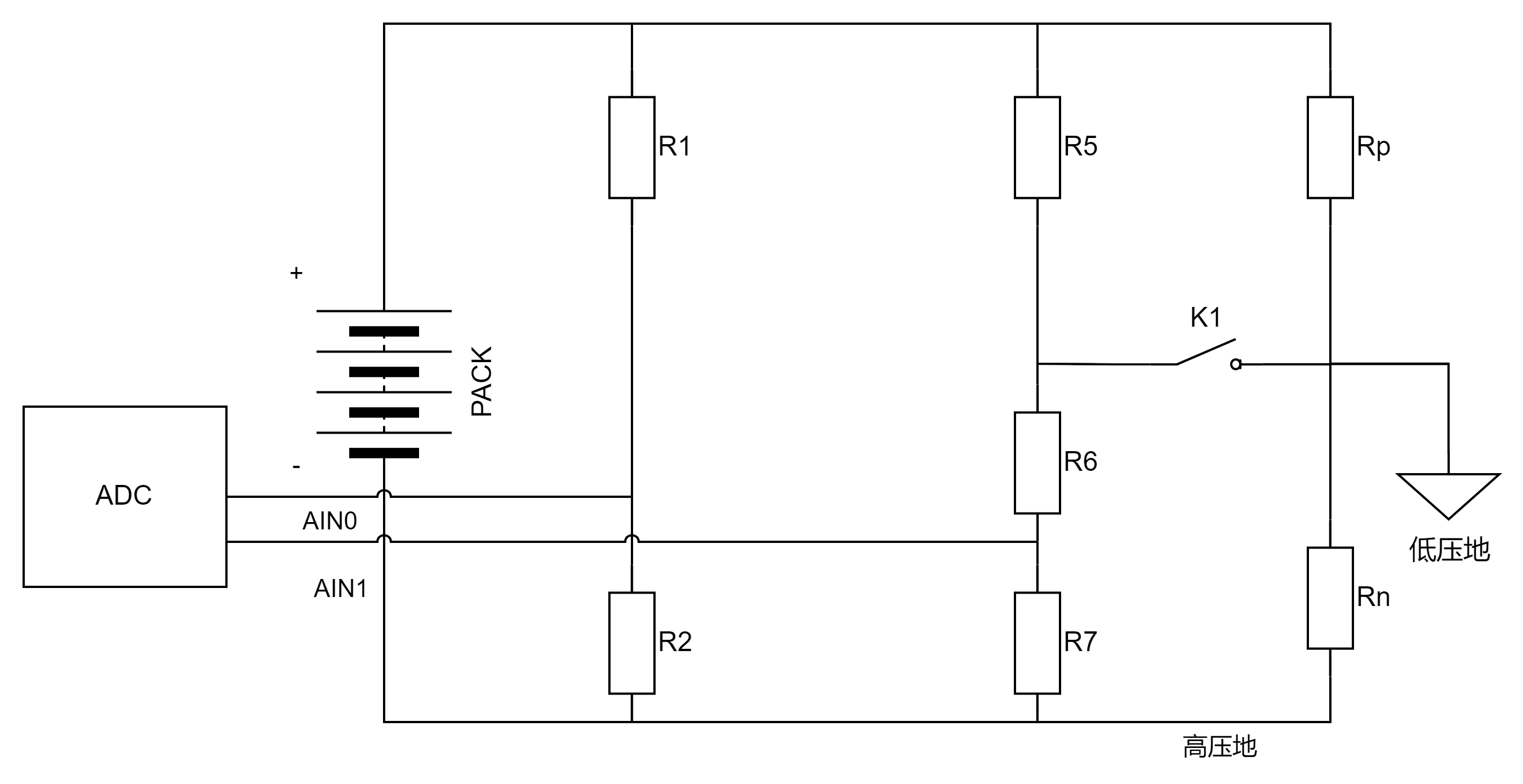
在这里插入图片描述
$\begin{aligned} & V_{p+} ：代表电池总压 \\ & V_{1} ：代表上桥臂电压，即 R_{5} 或 R_{p} 两端电压 \\ & V_{2} ：代表下桥臂电压，即（R_{6} + R_{7} ）两端电压或 R_{n} 两端电压 \\ & V_{AIN0} ：代表R_{2} 两端电压，从而推导出 V_{p+} \\ & V_{AIN1} ：代表R_{7} 两端电压，从而推导出 V_{2} \\ \end{aligned}$
根据已知条件列出公式：
$\begin{aligned} & V_{p+} = V_{AIN0} * \frac{ R_{1} + R_{2} }{R_{2}} \Longleftarrow V_{p+} = V_{AIN0} + \frac{ V_{AIN0}}{R_{2}}*R_{1} \\ & V_{2} = V_{AIN1} * \frac{ R_{6} + R_{7} }{R_{7}} \Longleftarrow V_{p+} = V_{AIN1} + \frac{ V_{AIN1}}{R_{7}}*R_{6} \\ & V_{1} = V_{p+} - V_{2} \\ & 由基尔霍夫电流定理（KCL）得 \\ \\ & \frac{ V_{1} }{R_{5}} + \frac{ V_{1} }{R_{p}} = \frac{ V_{AIN1} }{R_{7}} + \frac{ V_{2} }{R_{n}} \end{aligned}$

第二步：V1' 和 V2' 的采集与 Rn Rp 电阻的计算

国标中第一次检测出上下桥臂电压后,判断两个电压的大小,来决定第二次并入电阻的位置,即哪个位置电压大,第二次就在这个位置处并入已知电阻

若 V1 ≥ V2 ，闭合 K2，接入 PACK+ 侧辅助电阻 R3，重新测得高压地到低压地为 V2'，PACK+到高压地电压 Vp+'

根据已知条件列出公式：
$\begin{aligned} & V_{p+}' = V'_{AIN0} * \frac{ R_{1} + R_{2} }{R_{2}} \Longleftarrow V_{p+}' = V_{AIN0}' + \frac{ V_{AIN0}'}{R_{2}}*R_{1} \\ & V_{2}' = V_{AIN1}' * \frac{ R_{6} + R_{7} }{R_{7}} \Longleftarrow V_{p+}' = V_{AIN1}' + \frac{ V_{AIN1}'}{R_{7}}*R_{6} \\ & V_{1}' = V_{p+}' - V_{2}' \\ & 由基尔霍夫电流定理（KCL）得 \\ \\ & \frac{ V_{1}' }{R_{3}} + \frac{ V_{1}' }{R_{5}} + \frac{ V_{1}' }{R_{p}} = \frac{ V_{AIN1}' }{R_{7}} + \frac{ V_{2}' }{R_{n}} \end{aligned}$
联立方程：
$\begin{aligned} \begin{cases} \frac{ V_{1} }{R_{5}} + \frac{ V_{1} }{R_{p}} = \frac{ V_{AIN1} }{R_{7}} + \frac{ V_{2} }{R_{n}}\\ \frac{ V_{1}' }{R_{3}} + \frac{ V_{1}' }{R_{5}} + \frac{ V_{1}' }{R_{p}} = \frac{ V_{AIN1}' }{R_{7}} + \frac{ V_{2}' }{R_{n}}\\ \end{cases} \end{aligned}$
两个未知数，两个方程，求出 Rp Rn
若 V1 ＜ V2 ，闭合K3，接入 PACK+ 侧辅助电阻 R4，重新测得高压地到低压地为 V2'，PACK+到高压地电压 Vp+'

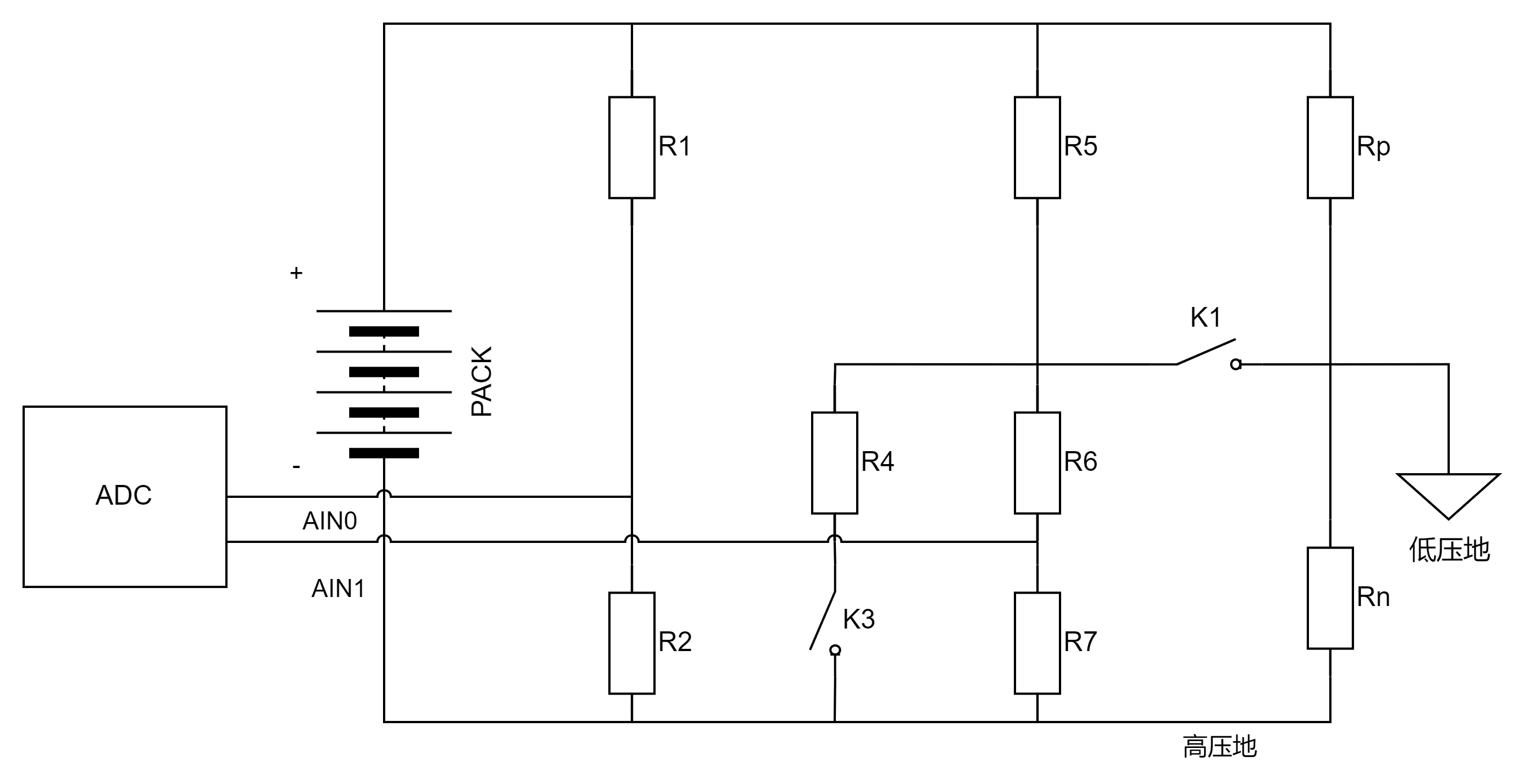
根据已知条件列出公式：
$\begin{aligned} & V_{p+}' = V'_{AIN0} * \frac{ R_{1} + R_{2} }{R_{2}} \Longleftarrow V_{p+}' = V_{AIN0}' + \frac{ V_{AIN0}'}{R_{2}}*R_{1} \\ & V_{2}' = V_{AIN1}' * \frac{ R_{6} + R_{7} }{R_{7}} \Longleftarrow V_{p+}' = V_{AIN1}' + \frac{ V_{AIN1}'}{R_{7}}*R_{6} \\ & V_{1}' = V_{p+}' - V_{2}' \\ & 由基尔霍夫电流定理（KCL）得 \\ \\ & \frac{ V_{1}' }{R_{5}} + \frac{ V_{1}' }{R_{p}} = \frac{ V_{AIN1}' }{R_{7}} + \frac{ V_{2}' }{R_{n}} + \frac{ V_{2}' }{R_{4}} \end{aligned}$
联立方程：
$\begin{aligned} \begin{cases} \frac{ V_{1} }{R_{5}} + \frac{ V_{1} }{R_{p}} = \frac{ V_{AIN1} }{R_{7}} + \frac{ V_{2} }{R_{n}}\\ \frac{ V_{1}' }{R_{5}} + \frac{ V_{1}' }{R_{p}} = \frac{ V_{AIN1}' }{R_{7}} + \frac{ V_{2}' }{R_{n}} + \frac{ V_{2}' }{R_{4}}\\ \end{cases} \end{aligned}$
两个未知数，两个方程，求出 Rp Rn