100个python算法超详细讲解：自守数

1．问题描述
自守数是指一个数的平方的尾数等于该数自身的自然数。例如，5^2
=25，25^2 =625，76^2 =5776，9376^2 =87 909 376。求100 000以内的自守
数。
2．问题分析
根据自守数的定义，求解本题的关键是知道当前所求自然数的位
数，以及该数平方的尾数与被乘数、乘数之间的关系。
3．算法设计
采用“求出一个数的平方后再截取最后相应位数”的方法显然是不可
取的，因为计算机无法表示过大的整数。
分析手工方式下整数平方（乘法）的计算过程，以376为例：

 本问题所关心的是积的最后三位。分析产生积的后三位的过程可以
看出，在每一次的部分积中，并不是它的每一位都会对积的后三位产生
影响。总结规律可以得到，在三位数乘法中，对积的后三位产生影响的
部分积分别如下：
·第一个部分积中：被乘数最后三位×乘数的倒数第一位。
·第二个部分积中：被乘数最后两位×乘数的倒数第二位。
·第三个部分积中：被乘数最后一位×乘数的倒数第三位。
将以上部分积的后三位求和后截取后三位就是三位数乘积的后三
位。这样的规律可以推广到同样问题的不同位数乘积。
4．求给定数的位数
求一个数的位数可以借助最高位的权值来计算，对于十进制来说，
个位的权值为10 0 ，十位的权值为10 1 ，百位的权值为10 2 ，以此类推。
一个存储三位数的变量n=123，每次除以10，将得到的值再赋给n，直到
n的值为0，最多可以除3次；若变量n中存储的是4位数，用同样的方法
去除以10最多可以除4次。可以发现，直到变量变为0，除以10的次数即
为当前给定数的位数。程序如下：

#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author : liuhefei
# @desc: 求给定数的位数
if __name__=="__main__":print("请输入一个正整数n：", end="")n = int(input())if n <=0:print("输出错误")exit()count = 0 # count存储数的位数while n != 0:n = n // 10count += 1print(" %d 位数" %count)

由于本题在下面的编程过程中还要用到原数number，故在求位数的
程序段中为保证number值不被破坏，暂时将number的值赋给另一变量
mul，即mul=number，由mul代替number去执行相应的操作。对应程序
段如下：

mul = number
k = 1
while (mul // 10) > 0: # 由number的位数确定截取数字进行乘法时的系数k
mul //= 10
k *= 10

5．分离给定数中的最后几位
从一个两位数（存在变量n中）开始分析，分离最低位个位：
n%10；对于三位数n，分离最后两位：n%100；对于四位数n，分离最
后三位：n%1000；以此类推，若分离出最后x位，只需要用原数对10x
求余。
从算法设计部分所举例子可以看出，对于第二个部分积“2632”来说
其实应该是“26320”，因为对于乘数中的倒数第二位“7”来说，因其在十
位，对应的权值为10，第二个部分积实质上为376×70=26 320。故求部
分积的程序段为：

while k > 0:
# (部分积+截取被乘数的后N位×截取乘数的第M位)，%a再截取部分积
mul = (mul + (number % (k * 10))*(number % b - number % (b // 10)))%a
k //= 10 # k为截取被乘数时的系数
b *= 10

对于整个循环来说，变量k是由number的位数确定截取数字进行乘
法时的系数。第一次执行循环体时，被乘数的所有位数都影响到平方的
尾数，故第一个部分的积等于被乘数×乘数的最后一位，将部分积累加
到变量mul上，再对a取余截取相应的尾数位数；第二次执行循环体，影
响平方尾数的是被乘数中除了最高位之外的数（故k先除以10再参加运
算），第二个部分的积等于被乘数×乘数的倒数第二位，(number%b-
number%(b//10))用来求乘数中影响平方尾数的对应位上的数；第三次、
第四次执行循环体的过程同上。
6．确定程序框架
该程序的简略流程图如图3.13所示。

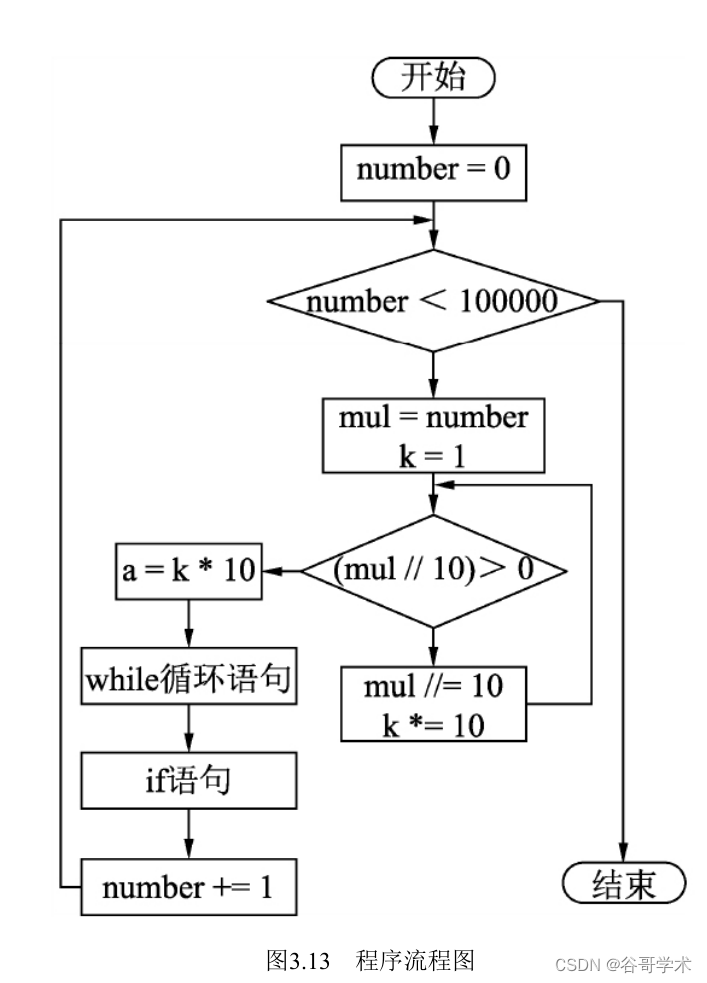
7．完整的程序

#!/usr/bin/python3
# -*- coding: utf-8 -*-
# @author : liuhefei
# @desc: 自守数
if __name__=="__main__":print("100000以内的自守数：")for number in range(0, 100000):mul = numberk = 1while (mul // 10) > 0: # 由number的位数确定截取数字进行乘法时的系数kmul //= 10k *= 10a = k * 10 # a为截取部分积时的系数mul = 0 # 积的最后n位b = 10 # b为截取乘数相应位时的系数while k > 0:# (部分积+截取被乘数的后N位×截取乘数的第M位)，%a再截取部分积mul = (mul + (number % (k * 10))*(number % b - number % (b // 10)))%ak //= 10 # k为截取被乘数时的系数b *= 10if number == mul: # 判定若为自守数，则输出print("%ld " %number, end="\t")# print()

 8．运行结果
在PyCharm中运行程序，运行结果如图3.14所示。