自守数专题
C语言例4-24:从键盘输入一个小于1000的自然数,判断其是否是自守数。
自守数是指一个数的平方的尾数等于其自身的自然数,例如25*25=625 代码如下: //从键盘输入一个小于1000的自然数,判断其是否是自守数。//自守数是指一个数的平方的尾数等于其自身的自然数,例如25*25=625//算法分析:由自守数的定义可知,自守数的平方与10或100或1000相除的余数是自守数本身#include<stdio.h>int main(void){int nu
B1091 N-自守数 (15 分)
如果某个数 K K K 的平方乘以 N N N 以后,结果的末尾几位数等于 K K K,那么就称这个数为“ N N N-自守数”。例如 3 × 9 2 2 = 25392 3×92^2=25392 3×922=25392,而 25392 25392 25392 的末尾两位正好是 92 92 92,所以 92 92 92 是一个 3 3 3-自守数。 本题就请你编写程序判断一
牛客算法题 HJ99 自守数 golang实现
题目 HJ99 自守数 描述自守数是指一个数的平方的尾数等于该数自身的自然数。例如:25^2 = 625,76^2 = 5776,9376^2 = 87909376。请求出n(包括n)以内的自守数的个数数据范围: 1≤�≤100001≤n≤10000 输入描述:int型整数输出描述:n以内自守数的数量。示例1输入:6复制输出:4复制说明:有0,1,5,6这四个自
华为机试HJ99 自守数
HJ99 自守数-Python 题目解题思路代码结果 题目 解题思路 1、多组输入,需要循环 2、n以内,从0到n,循环就要记得有n。循环判断平方后的字符串以n的字符串结尾,来判断是自守数。 代码 while True:try:n = int
100个python算法超详细讲解:自守数
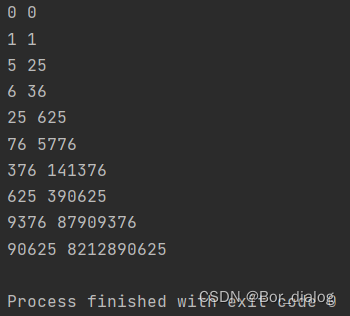
1.问题描述 自守数是指一个数的平方的尾数等于该数自身的自然数。例如,5^2 =25,25^2 =625,76^2 =5776,9376^2 =87 909 376。求100 000以内的自守 数。 2.问题分析 根据自守数的定义,求解本题的关键是知道当前所求自然数的位 数,以及该数平方的尾数与被乘数、乘数之间的关系。 3.算法设计 采用“求出一个数的平方后再截取最后相应位数”的方法显然是不可 取
python自守数问题 字符串切片解法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言直接上代码 前言 提示:这里可以添加本文要记录的大概内容: 自守数是指一个数的平方的尾数等于该数自身的自然数。例如:5^2=25,76 ^2=5776,此处的5和76就可以被称为自守数。通常我们求解自守数会通过观察平方后的尾数和乘数还有被乘数之间的关系来求解,但python 灵活的语法可
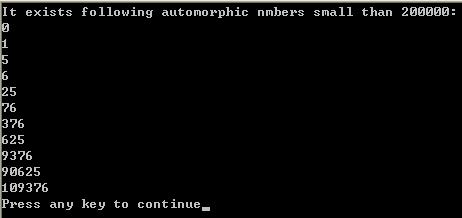
求200000以内自守数c语言,求c语言答案 输出200000以内的自守数
代码: #include int main() { long mul,number,k,ll,kk; printf("It exists following automorphic nmbers small than 200000:\n"); for(number=0;number<200000;number++) { for(mul=number,k=1;(mul/=10)>0;k*=10);