本文主要是介绍哈夫曼编码(霍夫曼、赫夫曼),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、发展历史
哈夫曼使用自底向上的方法构建二叉树。
哈夫曼编码的基本方法是先对图像数据扫描一遍,计算出各种像素出现的概率,按概率的大小指定不同长度的唯一码字(这种长度不同的编码方式称为变长编码,对应的长度相同的编码方式叫定长编码),由此得到一张该图像的哈夫曼码表。编码后的图像数据记录的是每个像素的码字,而码字与实际像素值的对应关系记录在码表中。
(同理也可对字符数据,扫描字符数据,计算各字符出现概率,按概率的大小指定不同长度的唯一码字,得到一段该字符数据的哈夫曼码表,编码后的字符数据记录是每个字符的码字,而码字与实际字符的对应关系记录在码表中)
该方法完全依据字符出现概率来构造异字头(即任一字符的编码不会是另一字符编码的前缀)的平均长度最短的码字,有时称之为最佳编码,一般就称Huffman编码。
二、原理
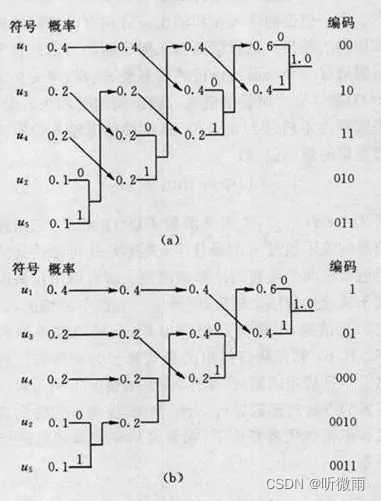
a图表示将新合并的支路排到等概率的最上支路,b图则是排到等概率的最下支路
设某信源产生有五种符号 u 1 , u 2 , u 3 , u 4 和 u 5 u_1,u_2,u_3,u_4和u_5 u1,u2,u3,u4和u5,对应概率 p 1 = 0.4 , p 2 = 0.1 , p 3 = p 4 = 0.2 , p 5 = 0.1 p_1=0.4,p_2=0.1,p_3=p_4=0.2,p_5=0.1 p1=0.4,p2=0.1,p3=p4=0.2,p5=0.1。首先,将符号按照概率由大到小排队,如图1所示。编码时,从最小概率的两个符号开始,可选其中一个支路为0,另一支路为1。这里,我们选上支路为0,下支路为1。再将已编码的两支路的概率合并,并重新排队。多次重复使用上述方法直到合并概率归一时为止。
从上图中(a)和(b)可以看出,两者虽平均码长相等,但同一符号可以有不同的码长,及编码方法并不唯一,其原因是两支路概率合并后重新排队时,可能出现几个支路概率相等,造成排队方法不唯一。一般,若将新合并后的支路排到等概率的最上支路,将有利于缩短码长方差,且编出的码更接近于等长码。 这里上图(a)的编码比(b)好。
哈夫曼码的码字(各符号的代码)是异前置码字,即任一码字不会是另一码字的前面部分,这使各码字可以连在一起传送,中间不需另加隔离符号,只要传送时不出错,收端仍可分离各个码字,不致混淆。
三、定理
哈夫曼编码的具体方法:先按出现的概率大小排队,把两个最小的概率相加,作为新的概率和剩余的概率重新排队,再把最小的两个概率相加,再重新排队,直到最后变成1。每次相加时都将“0”和“1”赋与相加的两个概率,读出时由该符号开始一直走到最后的“1”, 将路线上所遇到的“0”和“1”按最低位到最高位的顺序排好,就是该符号的赫夫曼编码。
3.1 举例
U :( a 1 , a 2 , a 3 , a 4 , a 5 , a 6 , a 7 ) U:(a_1,a_2,a_3,a_4,a_5,a_6,a_7) U:(a1,a2,a3,a4,a5,a6,a7)
值分别为:
( 0.20 0.20 0.20 0.19 0.19 0.19 0.18 0.18 0.18 0.17 0.17 0.17 0.15 0.15 0.15 0.10 0.10 0.10 0.01 0.01 0.01)
生成的哈哈夫曼树如下:
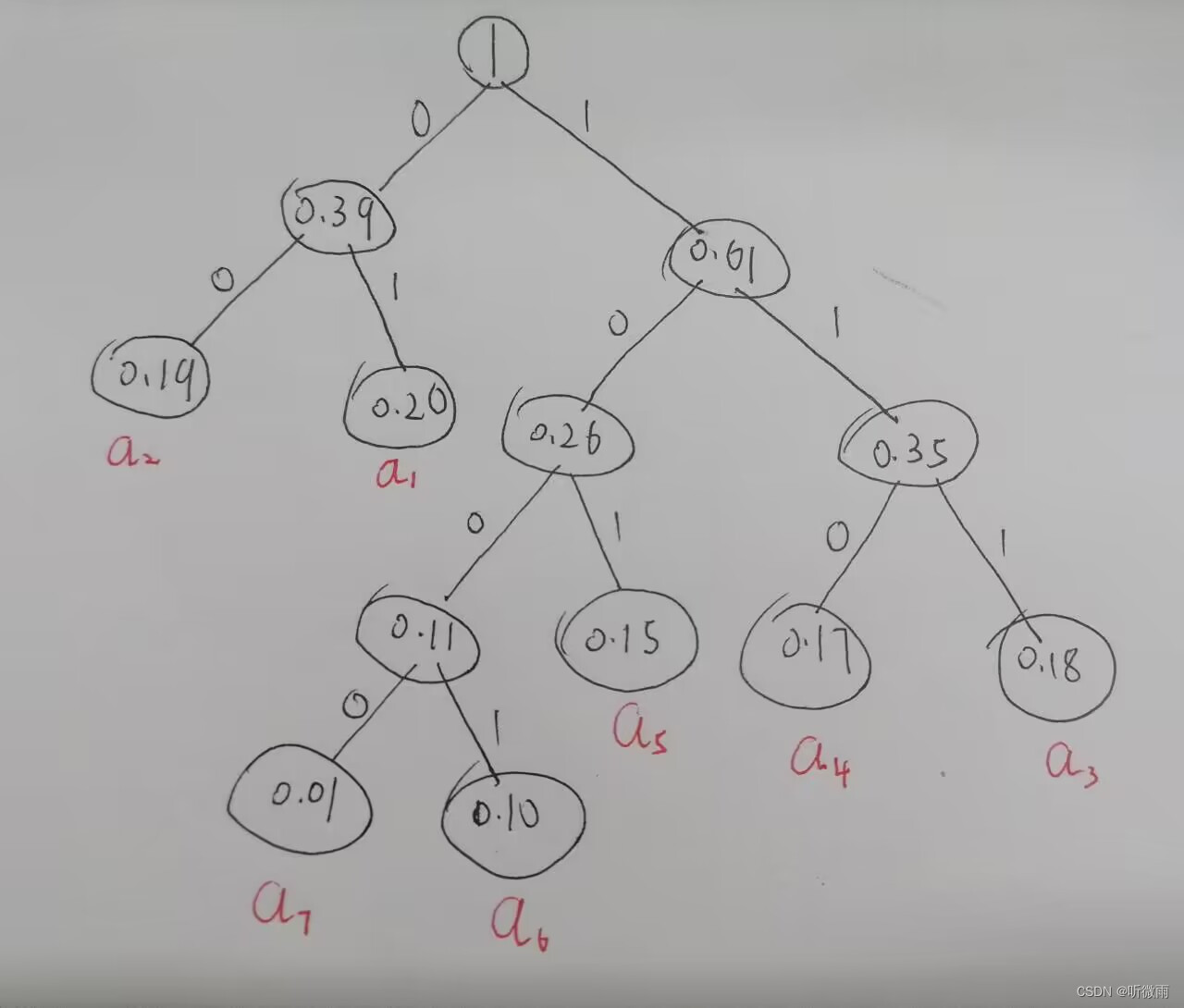
哈夫曼编码为:
a 1 a_1 a1:01
a 2 a_2 a2:00
a 3 a_3 a3:111
a 4 a_4 a4:110
a 5 a_5 a5:101
a 6 a_6 a6:1000
a 7 a_7 a7:1001
用赫夫曼编码所得的平均比特率: ∑ 码长 ∗ 出现概率 \sum码长 *出现概率 ∑码长∗出现概率
上例为:0.2 * 2+0.19 * 2+0.18 * 3+0.17 * 3+0.15 * 3+0.1 * 4+0.01 *4=2.72bit
四、类型
4.1 静态哈夫曼编码
1.哈夫曼编码时如何实现数据的压缩和解压缩的呢?
在计算机当中,数据的存储和加工都是以字节为基本单位的,一个西文字符要通过一个字节来表示,而一个汉字就要用两个字节,我们把这种每一个字符都通过相同的字节数来表达的编码形式称为定长编码。
以西文为例,例如我们要在计算机当中存储这样一句话:I am a teacher. 就需要15个字节,也就是120(15*8)个二进制位的数据来实现。
与这种定长编码不同的是,哈夫曼编码是一种变长编码,它根据字符出现的概率来构造平均长度最短的编码,也就是说,如果一个字符在一段文档当中出现的次数多,它的编码就响应的短,如果一个字符在一段文档当中出现的次数少,它的编码就相应的长。当编码中,各码字的长度严格按照对应符号出现的概率大小进行逆序排列时,则编码的平均长度时最小的,这就是哈夫曼编码实现数据压缩的基本原理。
2.获取一段数据的哈夫曼编码三步骤
1.扫描需编码的数据,统计原数据中各字符出现的概率。
2.利用得到的概率值创建哈夫曼树。
3.对哈夫曼树进行编码,并把编码后得到的码字存储起来。
3.如何保证任意一个字符的编码都不会成为其他编码的前缀呢?(方便接收端的译码过程)
因为定长编码已经用相同的位数这个条件保证了任一字符的编码都不会成为其它编码的前缀,所以某一字符的编码成为另一字符编码前缀这种情况只会出现在变长编码中,要想避免这种情况,必须用一个条件来制约变长编码,这个条件就是要想成为压缩编码,变长编码就必须是前缀编码(任一字符的编码不能是另一字符编码的前缀)。
那么哈夫曼编码是否是前缀编码呢?观察上图由 ( a 1 , a 2 , a 3 , a 4 , a 5 , a 6 , a 7 ) (a_1,a_2,a_3,a_4,a_5,a_6,a_7) (a1,a2,a3,a4,a5,a6,a7)构成的编码树,可以发现要想成为某一字符的编码前缀,必须是该字符的父亲节点、祖孙节点…等有辈分差关系的节点。在哈夫曼树中,文档中的数据字符全都分布在哈夫曼树的叶子节点,从而保证了哈夫曼编码当中的任何一个字符都不能是另一个字符编码的前缀,也就是说哈夫曼编码是一种前缀编码,也就保证了解压缩过程当中译码的准确性。
4.哈夫曼编码的解压缩过程
将编码严格按照哈夫曼树进行翻译就可以了,例如遇到1000,就可以顺着哈夫曼树找到 a 6 a_6 a6,遇到111,就可以顺着哈夫曼树找到 a 3 a_3 a3,以此类推,就可以很顺利的找到原来所有的字符。
5.哈夫曼编码的重要性
哈夫曼编码是一种一致性编码,有着非常广泛的应用,例如在JPEG文件中,就应用了哈夫曼编码来实现最后一步的压缩,在数字电视大力发展的今天,哈夫曼编码成为了视频信号的主要压缩方式。哈夫曼编码出现结束了熵编码不能实现最短编码的历史,也使哈夫曼编码成为一种非常重要的无损编码。
6.静态哈夫曼方法的缺点
静态哈夫曼编码的最大缺点就是它需要对原始数据进行两遍扫描:
- 第一遍统计原始数据中各字符出现的频率,利用得到的频率值创建哈夫曼树并将树的有关信息保存起来,便于压缩时使用;
- 第二遍则根据前面得到的哈夫曼树对原始数据进行编码,并将编码信息存储起来。这样如果用于网络通信中,将会引起较大的时延。
对于文件压缩这样的应用场合,额外的磁盘访问将会降低该算法的数据压缩速度。
4.2 动态哈夫曼编码(适应性哈夫曼编码)
动态哈夫曼编码允许在符号正在传输时构建代码,允许一次编码并适应数据中变化的条件,即随着数据流的到达,动态地收集和更新符号的概率(频率) 。一遍扫描的好处是使得源程序可以实时编码,但由于单个丢失会损坏整个代码,因此它对传输错误更加敏感。
动态哈夫曼编码与解码过程的链接:https://blog.csdn.net/weixin_43838265/article/details/117324663
动态哈夫曼编码方法对数据编码的依据是动态变化的哈夫曼树,也就是说,对于第n+1个字符编码时根据原始数据中前n个字符得到的哈夫曼树来进行的,压缩和解压具有相同的初始化树,每处理完一个字符,压缩和解压方使用相同的算法修改哈夫曼树,因而该方法不需要为解压而保存树的有关信息。压缩和解压一个字符所需的时间与该字符的编码长度成正比,因而该过程可以实时进行。
五、应用举例
哈夫曼树─即最优二叉树,带权路径长度最小的二叉树,经常应用于数据压缩。 在计算机信息处理中,“哈夫曼编码”是一种一致性编码法(又称“熵编码法”),用于数据的无损耗压缩。这一术语是指使用一张特殊的编码表将源字符(例如某文件中的一个符号)进行编码。这张编码表的特殊之处在于,它是根据每一个源字符出现的估算概率而建立起来的(出现概率高的字符使用较短的编码,反之出现概率低的则使用较长的编码,这便使编码之后的字符串的平均期望长度降低,从而达到无损压缩数据的目的)。这种方法是由David.A.Huffman发展起来的。 例如,在英文中,e的出现概率很高,而z的出现概率则最低。当利用哈夫曼编码对一篇英文进行压缩时,e极有可能用一个位(bit)来表示,而z则可能花去25个位。用普通的表示方法时,每个英文字母均占用一个字节(byte),即8个位。二者相比,e使用了一般编码的1/8的长度,z则使用了3倍多。若能实现对于英文中各个字母出现概率的较准确的估算,就可以大幅度提高无损压缩的比例。
这篇关于哈夫曼编码(霍夫曼、赫夫曼)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






