本文主要是介绍梅科尔工作室-SVM培训,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.SVM与KNN的区别
svm:
就像是在河北和北京之间有一条边界线,如果一个人居住在北京一侧就预测为北京人,在河北一侧,就预测为河北人。但是住在河北的北京人和住在北京的河北人就会被误判。
svm需要超平面wx+b来分割数据集(此处以线性可分为例),因此会有一个模型训练过程来找到w和b的值。训练完成之后就可以拿去预测了,根据函数y=wx+b的值来确定样本点x的label,不需要再考虑训练集。对于SVM,是先在训练集上训练一个模型,然后用这个模型直接对测试集进行分类。

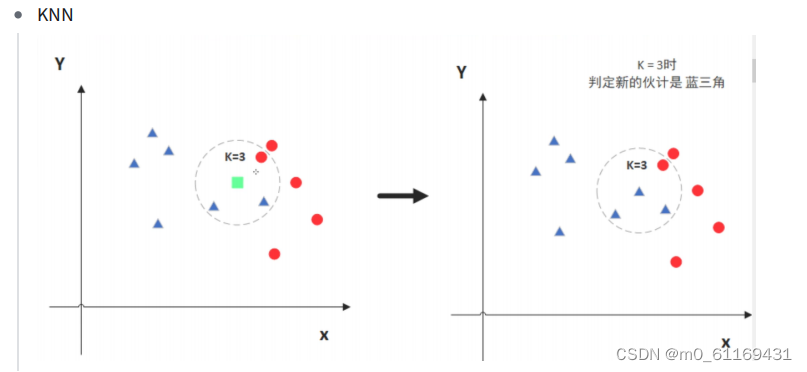
knn:
就是物以类聚,人以群分。如果你的朋友里大部分是北京人,就预测你也是北京人。如果你的朋友里大部分是河北人,那就预测你是河北人。不管你住哪里。
knn没有训练过程,他的基本原理就是找到训练数据集里面离需要预测的样本点距离最近的k个值(距离可以使用比如欧式距离,k的值需要自己调参),然后把这k个点的label做个投票,选出一个label做为预测。对于KNN,没有训练过程。只是将训练数据与训练数据进行距离度量来实现分类。
2.SVM原理
SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。如下图所示, w⋅x+b=0 即为分离超平面,对于线性可分的数据集来说,这样的超平面有无穷多个(即感知机),但是几何间隔最大的分离超平面却是唯一的。
2.1 寻找最大间隔
既然这样的直线是存在的,那么我们怎样寻找出这样的直线呢?与二维空间类似,超平面的方程也可以写成一下形式:
![]()
有了超平面的表达式之后之后,我们就可以计算样本点到平面的距离了。假设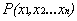

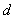
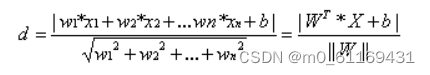
其中||W||为超平面的范数,常数b类似于直线方程中的截距。
这是一个有约束条件的优化问题,通常我们可以用拉格朗日乘子法来求解。拉格朗日乘子法的介绍可以参考这篇博客。应用拉格朗日乘子法如下:
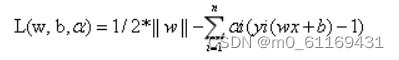
求L关于求偏导数得: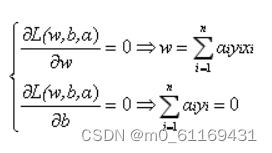
2.2 松弛变量
由于实际中很多样本数据都不能够用一个超平面把数据完全分开。如果数据集中存在噪点的话,那么在求超平的时候就会出现很大问题。从图三中课看出其中一个蓝点偏差太大,如果把它作为支持向量的话所求出来的margin就会比不算入它时要小得多。更糟糕的情况是如果这个蓝点落在了红点之间那么就找不出超平面了。
因此引入一个松弛变量ξ来允许一些数据可以处于分隔面错误的一侧。这时新的约束条件变为:
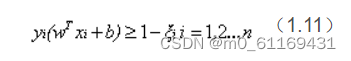
式中ξi的含义为允许第i个数据点允许偏离的间隔。如果让ξ任意大的话,那么任意的超平面都是符合条件的了。所以在原有目标的基础之上,我们也尽可能的让ξ的总量也尽可能地小。所以新的目标函数变为:
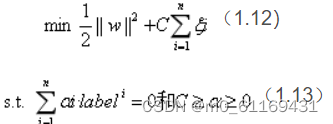
新的拉格朗日函数变为:
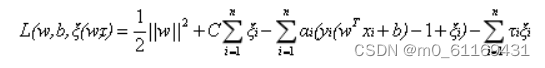
代入原式化简之后得到和原来一样的目标函数:
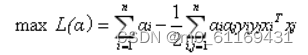
经过添加松弛变量的方法,我们现在能够解决数据更加混乱的问题。通过修改参数C,我们可以得到不同的结果而C的大小到底取多少比较合适,需要根据实际问题进行调节。
2.3 核函数
以上讨论的都是在线性可分情况进行讨论的,但是实际问题中给出的数据并不是都是线性可分的。
事实上,对于低维平面内不可分的数据,放在一个高维空间中去就有可能变得可分。以二维平面的数据为例,我们可以通过找到一个映射将二维平面的点放到三维平面之中。理论上任意的数据样本都能够找到一个合适的映射使得这些在低维空间不能划分的样本到高维空间中之后能够线性可分。我们再来看一下之前的目标函数:
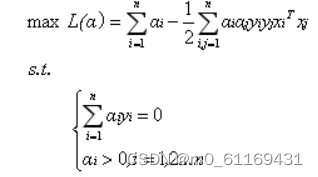
定义一个映射使得将所有映射到更高维空间之后等价于求解上述问题的对偶问题:

当特征变量非常多的时候在,高维空间中计算内积的运算量是非常庞大的。考虑到我们的目的并不是为找到这样一个映射而是为了计算其在高维空间的内积,因此如果我们能够找到计算高维空间下内积的公式,那么就能够避免这样庞大的计算量,我们的问题也就解决了。实际上这就是我们要找的核函数,即两个向量在隐式映射后的空间中的内积。
常用核函数表:
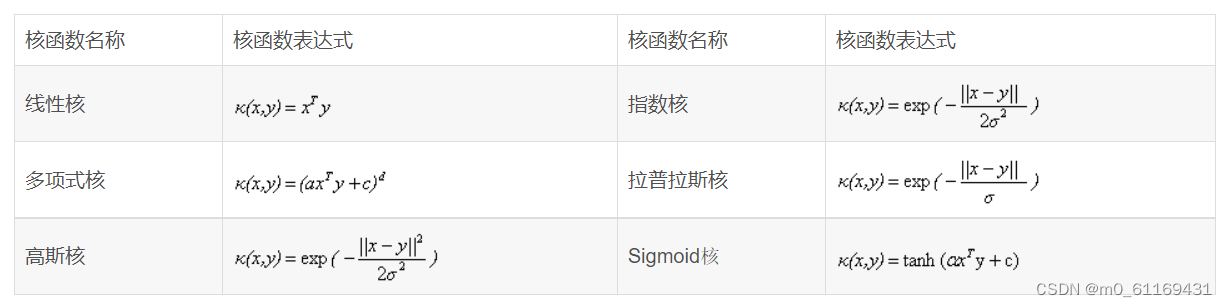
3. 飞浆运行截图
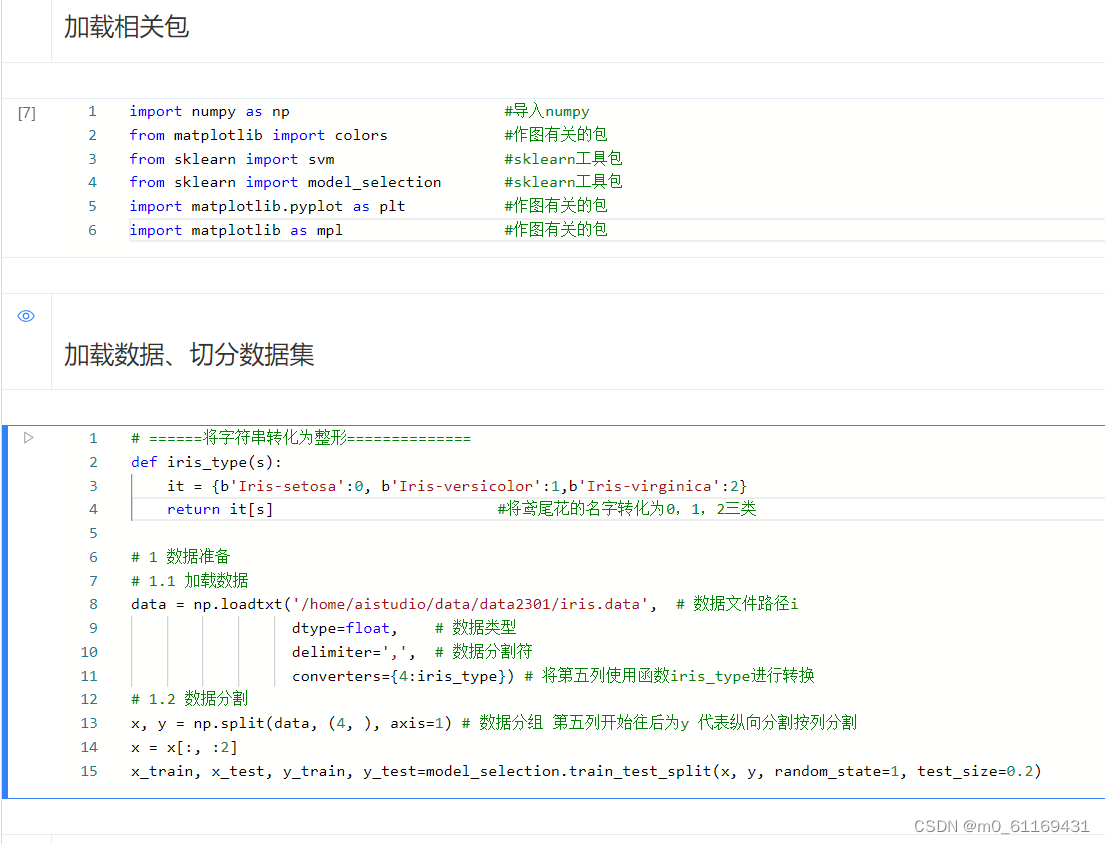
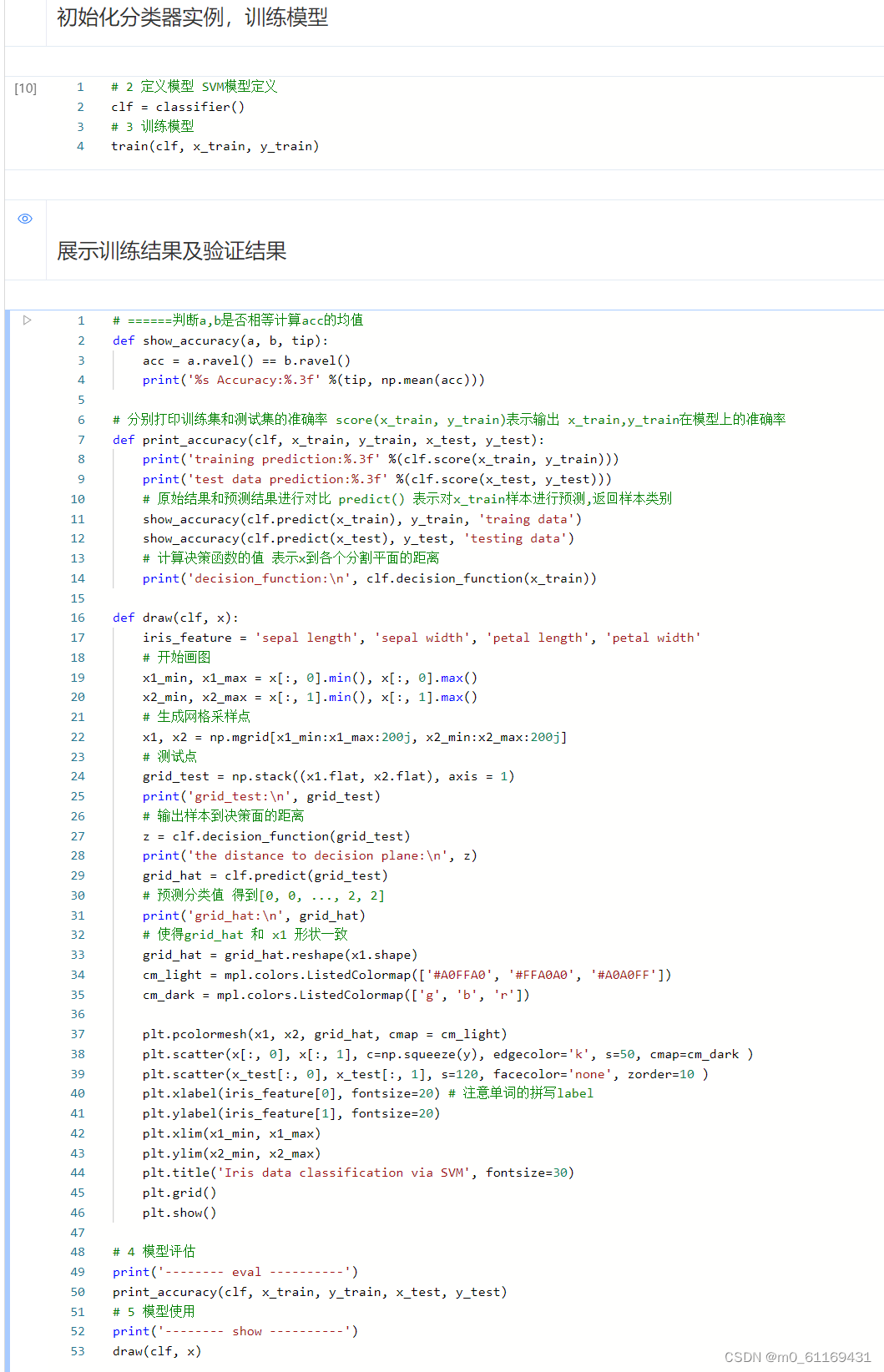
这篇关于梅科尔工作室-SVM培训的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








