✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
⛄ 内容介绍
4 连杆机器人的运动学模拟器,演示:
- 机器人的硬编码行走。
- 反向运动学控制。
- 通过 Arduino 与物理机器人交互进行卡尔曼滤波
- Q-Learning,从一个位置移动到另一个位置,同时保持稳定并避开障碍物。
- 模拟退火,从一个位置移动到另一个位置,同时保持稳定并避开障碍物。
- 模拟退火向前走,避开遇到的障碍物。


⛄ 部分代码
function fixed2(phiVec,lVec,mVec,pos2,footsep,corners)
%%draws/re-draws robot position with foot 2 fixed.
%Colours background red for any collisions/instabilities
%keep track of lines to be deleted later
initialchildno = length(get(gca,'children'));
%% Initialise animation
switch nargin
case 5
lineObj = animInit();
animation(phiVec,lVec,mVec,lineObj,pos2,footsep,initialchildno);
case 6
lineObj = animInit(corners);
animation(phiVec,lVec,mVec,lineObj,pos2,footsep,initialchildno,corners);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Local functions %%
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Animation initialisation
function lineObj = animInit(corners)
lWin = 5.0; %window size
figure(1)
hold on
axis equal
axis([-5 5 -0.4 6])
% Ground plot
plot([-lWin lWin],[0 0],'k','LineWidth',2)
%Underground lines
for j = 1:30
k = -lWin-1+j*2*lWin/20;
plot([k;k+0.2],[0;-0.2],'k','LineWidth',2)
end
if nargin == 1
%Grid added
gridinitialise([-5;5],30,[0;6],30);
%Obstacle added
for i = 1:length(corners)/2
obstenter(corners(:,2*i-1:2*i))
end
end
%link line objects
lineObj.h1 = line(0,0,'color','k','LineWidth',3);
lineObj.h2 = line(0,0,'color','k','LineWidth',3);
lineObj.h3 = line(0,0,'color','k','LineWidth',3);
lineObj.h4 = line(0,0,'color','k','LineWidth',3);
%foot line objects
lineObj.f1 = line(0,0,'color','k','LineWidth',3);
lineObj.f2 = line(0,0,'color','k','LineWidth',3);
%joint line objects
lineObj.d1 = line(0,0,'color','k','LineWidth',5,'Marker','o');
lineObj.d2 = line(0,0,'color','k','LineWidth',5,'Marker','o');
lineObj.d3 = line(0,0,'color','k','LineWidth',5,'Marker','o');
%centre of mass line object
lineObj.com = line(0,0,'color','r','LineWidth',3,'Marker','o');
end
rMat = rmat2calc(phiVec,lVec,pos2);
r00 = rMat(:,1);
r11 = rMat(:,2);
r22 = rMat(:,3);
r33 = rMat(:,4);
r44 = rMat(:,5);
rf1 = rMat(:,6);
rf2 = rMat(:,7);
[ground, ~] = throughground(rMat);
scollide = selfcollide(rMat,footsep);
com = centreofmass(mVec,rMat);
unstable = stability(com,pos2,0,lVec,2);
ocoll = 0;
if nargin == 8
for i = 1:length(corners)/2
if obstaclecollide(rMat,corners(:,2*i-1:2*i))
ocoll = 1;
end
end
end
%set position
set(lineObj.h1,'xdata',[r00(1) r11(1)],'ydata',[r00(2) r11(2)])
set(lineObj.h2,'xdata',[r11(1) r22(1)],'ydata',[r11(2) r22(2)])
set(lineObj.h3,'xdata',[r22(1) r33(1)],'ydata',[r22(2) r33(2)])
set(lineObj.h4,'xdata',[r33(1) pos2(1)],'ydata',[r33(2) pos2(2)])
set(lineObj.f1,'xdata',[r00(1) rf1(1)],'ydata',[r00(2) rf1(2)])
set(lineObj.f2,'xdata',[pos2(1) rf2(1)],'ydata',[pos2(2) rf2(2)])
set(lineObj.d1,'xdata',r11(1),'ydata',r11(2))
set(lineObj.d2,'xdata',r22(1),'ydata',r22(2))
set(lineObj.d3,'xdata',r33(1),'ydata',r33(2))
set(lineObj.com,'xdata',com(1),'ydata',com(2))
if ground == 1 || scollide == 1 || unstable == 1 || ocoll == 1
set(gcf,'color','r');
else
set(gcf,'color','w');
end
drawnow
%delete previous iteration
children = get(gca, 'children');
delete(children(end-initialchildno+1:end));
end
end
%returns array of fifth order polynomial given the start and end points
t0 = 1;
f = start;
coeff = [t0^5, t0^4, t0^3; 5*t0^4, 4*t0^3, 3*t0^2; 20*t0^3, 12*t0^2, 6*t0];
values5 = coeff^(-1)*[finish - start; 0; 0];
a = values5(1);
b = values5(2);
c = values5(3);
smoothout = zeros(p,1);
for i = 1:1:p
x = a*(i*t0/p)^5 + b*(i*t0/p)^4 + c*(i*t0/p)^3 + f;
if x > 1
x = 1;
end
if x < 0
x = 0;
end
smoothout(i) = x;
end
end
⛄ 运行结果

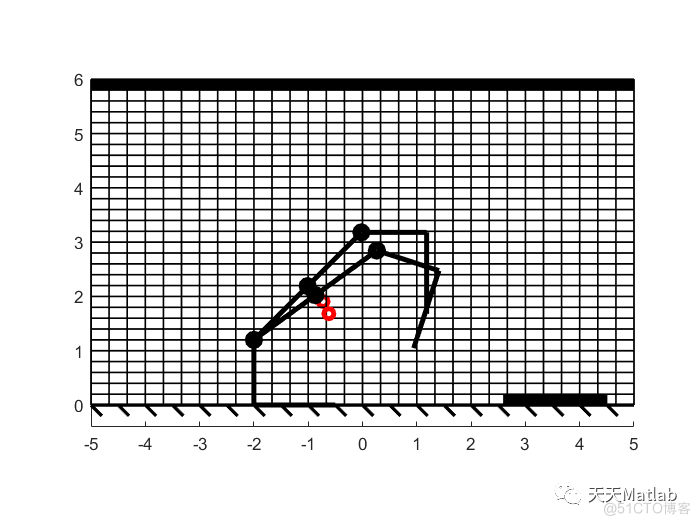
⛄ 参考文献
[1]葛建兵, 翟雪琴, 窦进强,等. 基于MATLAB的机器人运动学仿真[J]. 机械设计与制造, 2008.









