本文主要是介绍重拾线形代数的记忆,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
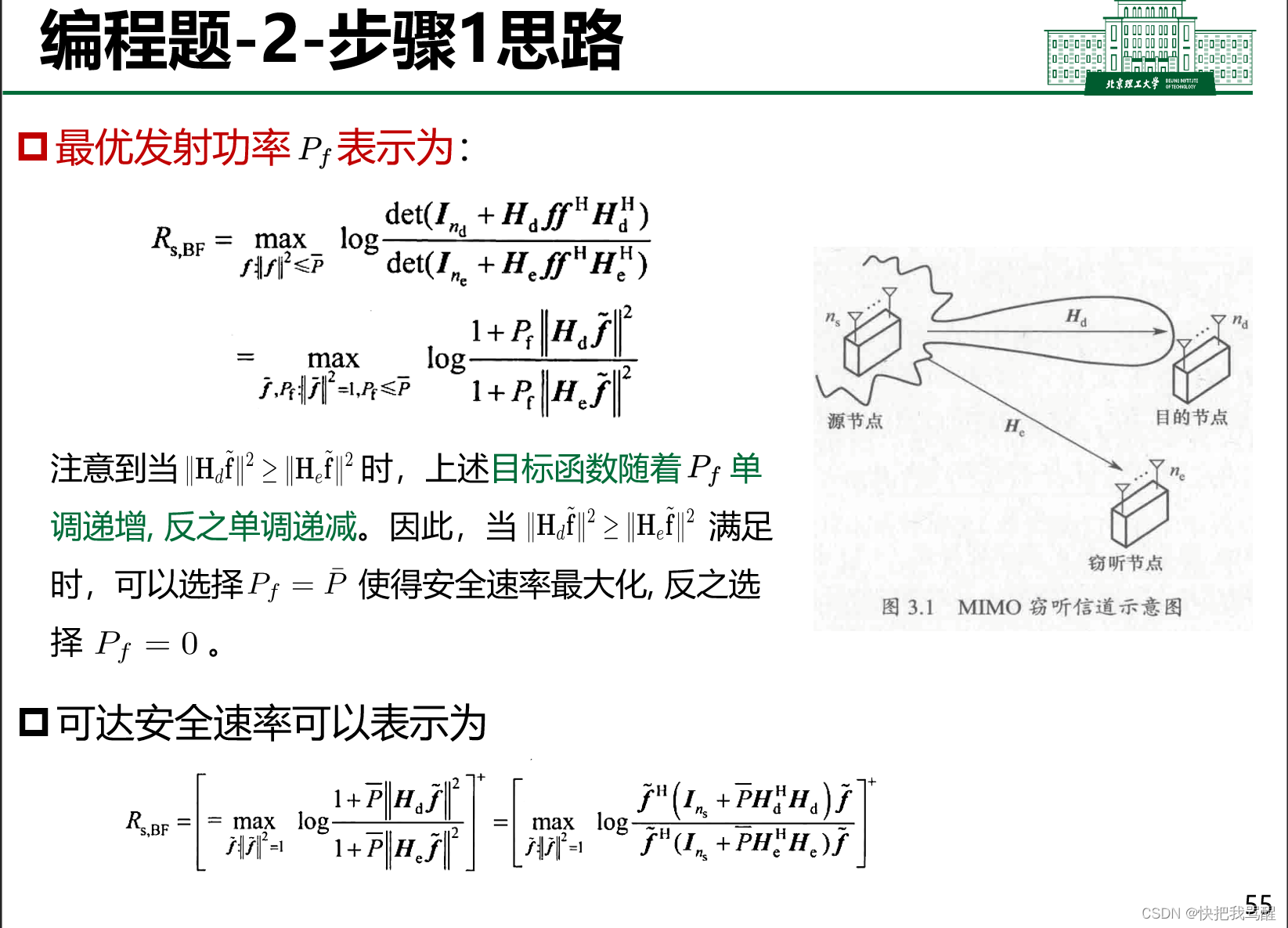
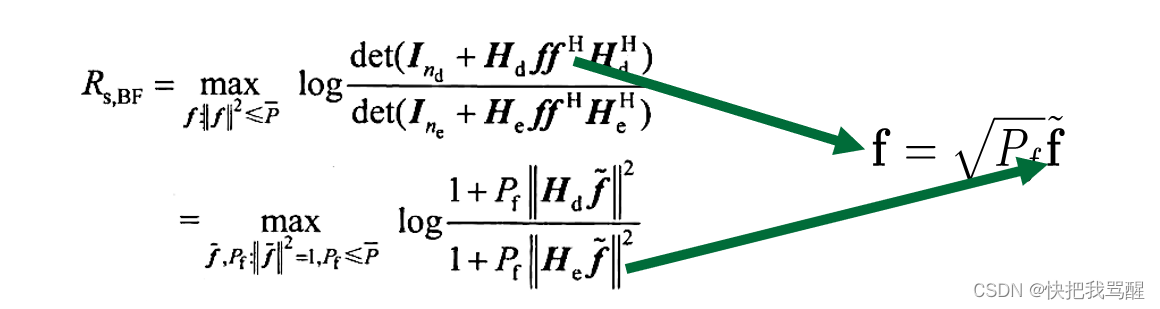
关于这里面上下为什么相等起了疑惑(线形代数还给老师了):
证明:
I是单位阵,u是列向量,加撇表共轭转置。
考虑U = u u’ 的特征系统:
- u ⟂ x时,U x = 0 = 0 x。
- u ∥ x 时,U x = … = |u|^2 x。
可见有单重特征值 |u|^2,其余特征值都是 0。(U = u u’ 这种特征系统Rank一定为1)
考虑 I + U,它有单重特征值 |u|^2 + 1,其余特征值都是1。行列式等于特征值之积,即 1 + |u|^2。
在图中,u = H f,然后又归一化了一下f。
这篇关于重拾线形代数的记忆的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!