泰坦尼克沉船存活率（机器学习，Python）

目录

1，实验要求：

2，报告内容

引言

数据处理

导入数据

查看数据集信息

数据清洗

 特征工程

特征提取

特征选择

生还率预测说明

模型构建

建立训练数据集和测试数据集

 选择不同的机器学习算法

训练模型，评估模型

 方案实施

生存预测

参数调优

结论

改进方法

---

1，实验要求：

详细描述：按照机器学习一般流程针对“泰坦尼克沉船生存率”数据进行数据分析和获救预测。

要求：

(1)数据预处理：对数据进行探索，查询是否有缺省值，以及对应的处理办法；

1. 数据划分训练集和测试集（train含有标签，test不含标签无法用来训练和测试，只能最后进行结果输出，所以要对train数据集进行划分）；
2. 数据分析：探索数据中各个属性和存活率（是否获救）的关系，并给出对应的关系图，如船上成员中性别分布，年龄分布等；性别、 不同船舱与存活率的关系；年龄、票价与存活率的关系等。最后根据各种关系图给出与存活率有关的属性（特征提取）有哪些并说明原因；
3. 搭建分类模型，对提取后的特征和标签（是否获救）建立模型并训练，并用训练好的模型对test数据集（前面划分的测试集和给出的test数据集）进行分类预测；
4. 对所选模型的超参数进行调节（使用网格搜索+CV或者手动调节），手动调节需给出至少三组参数取值以及对应的结果，根据结果分析出选择该组超参数的原因；
5. 每一步要详细并给出程序结果并给出相应的解释

2，报告内容

（该实验会以实验报告的形式上传，也是本人的期末大作业，如果有人想要借鉴我的文章非常荣幸，但是记得要去认真理解，并且加入自己的理解和一些实验的步骤就更好了）

引言

起于悲剧，止于浪漫。泰坦尼克号的沉船事件是历史上最为著名的海难事件之一，也是人类历史上的一次巨大悲剧。在1912年的这场事故中，超过1500人丧生，其中包括乘客和船员。这场事故震惊了全世界，引起了人们对船舶安全的广泛关注和讨论。

自那以后，人们一直在探索如何预防这类事件的发生，以及如何提高船舶的安全性。在现代科技的帮助下，我们可以利用机器学习技术来预测泰坦尼克号上乘客的存活率，以帮助我们更好地理解这场悲剧，并从中汲取经验教训。

本报告将结合泰坦尼克号的历史数据和机器学习算法来分析泰坦尼克号上乘客的存活率。我们将使用Python编程语言和一些常见的机器学习库，如Pandas、NumPy和Scikit-learn等。通过建立一个分类模型，我们将尝试预测哪些乘客在这场事故中存活下来的可能性更高。

在这个研究中，我们将探讨许多因素，如性别、客舱级别、乘客姓名（身份）、客舱号、家庭情况等，这些因素可能会影响乘客的生存几率。我们将使用这些特征来训练模型，以预测哪些乘客在船沉没时能够生还。

通过这个研究，我们可以更好地了解泰坦尼克号上的乘客，以及他们在这场悲剧中所面临的困境。我们也可以更好地理解机器学习技术在预测人类行为方面的应用和局限性。最重要的是，我们可以从这个研究中汲取经验教训，以帮助我们更好地预防类似事故的发生，并提高船舶的安全性。

在接下来的报告中，我们将介绍数据的收集和处理、特征工程、模型选择、模型评估等方面的内容。我们将尽力提供清晰的解释和详细的代码实现，以便读者能够更好地理解我们的方法和结果。我们希望这个研究能够为人们提供更多关于泰坦尼克号的历史信息，也能够帮助人们更好地了解机器学习技术的应用和局限性。

数据处理

导入数据

        首先我们将训练数据和测试数据进行纵向的堆叠，方便处理数据。

# 导入数据
from matplotlib import pyplot as plttrain = pd.read_csv('train.csv')
test = pd.read_csv('test.csv')
# 合并数据集，方便同时对两个数据进行清洗
full = pd.concat([train, test], ignore_index=True)
# 合并后的数据集，进行纵向堆叠
# print(full.shape)

 合并后的数据集为full（1309，12）

查看数据集信息

        查询的数据集需要具有和原始训练集相同的特征。包括乘客的个人信息、船票信息、登船港口、舱位等等。

        首先我们需要查看是否存在缺失值：

print(full.isnull().sum())

 然后得到结果

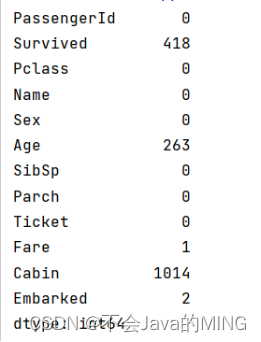
        根据上图给出的缺失值，其中，Age（年龄）缺少了263条，Fare（船票价格）缺少了1条，Embaeked（登船港口）缺少了2条，Cabin（船舱号）缺少了1014条，缺失比较大。如今，得知了缺失值，就要对其进行数据清洗。

数据清洗

1，数据预处理

        1.1，对于年龄和船票价格是数值类型，我们使用平均数来填充缺失值：

full['Age'] = full['Age'].fillna(full['Age'].mean())
# 船票价格
full['Fare'] = full['Fare'].fillna(full['Fare'].mean())
# 输出
# print(full.isnull().sum())

        1.2，对于登船港口，分别计算出类别的数量，采用最常见的类别进行填充：

# 登船港口
# 查看每一个类别的数量
# print(full['Embarked'].value_counts())
# 根据结果，S最常见，将缺失值设置为S
full['Embarked'] = full['Embarked'].fillna('S')
# print(full.isnull().sum())
# 船舱号
full['Cabin'] = full['Cabin'].fillna('U')
# print(full.isnull().sum())

        对于登船港口，查到的是，S为最常出现的值，所以我们将该值为缺失值填充。

        1.3，对于船舱号，由于缺失值太多，我们使用U来代替，表示未知

 特征工程

特征提取

        对于特征提取，首先要做的就是对数据的分类，对于有直接类别的数据还有字符串类型的数据进行了不同方式的处理。

1，有直接类别

Sex（性别）：男male，女female

# 性别
# print(full['Sex'].head())
sex_mapDict = {'male': 1,'female': 0}
full['Sex'] = full['Sex'].map(sex_mapDict)
# print(full['Sex'])

2，有直接类别的字符串类型

Embarked（登船港口）

S，C，Q

使用get_dummies进行one—hot编码，产生虚拟变量：

# 登船港口
embarkedDf = pd.DataFrame()
embarkedDf = pd.get_dummies(full['Embarked'], prefix='Embarked')
# 提取后的特征
# print(embarkedDf.head())
# 添加one-hot编码，产生虚拟变量到泰坦尼克号数据集
full = pd.concat([full, embarkedDf], axis=1)
# print(full.head())
# 把登船港口删掉
full.drop('Embarked', axis=1, inplace=True)
# print(full.head())

其中对S，C，Q成功分类：

 

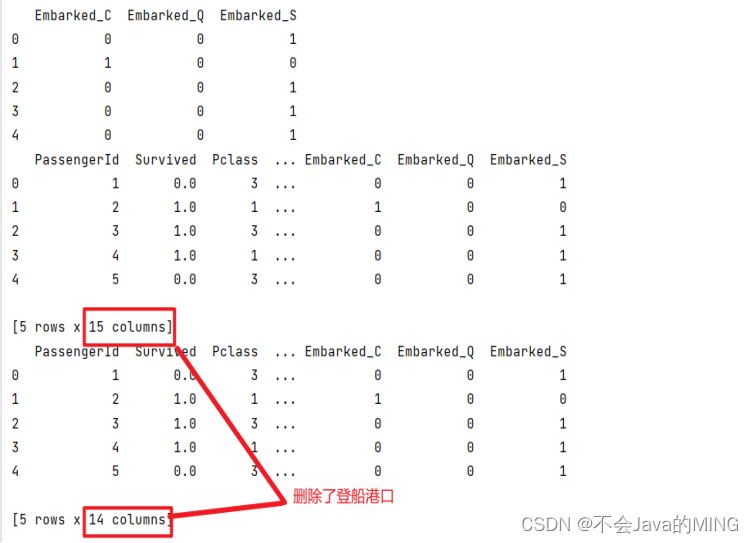
Pclass（客舱等级）：

该分类的方法和登船港口的方式相同：

# 船舱等级
pclassDf = pd.DataFrame()
pclassDf = pd.get_dummies(full['Pclass'], prefix='Pclass')
# 提取后的特征
# print(pclassDf.head())
# 添加one-hot编码，产生虚拟变量到泰坦尼克号数据集
full = pd.concat([full, pclassDf], axis=1)
# print(full.head())
full.drop('Pclass', axis=1, inplace=True)
# print(full.head())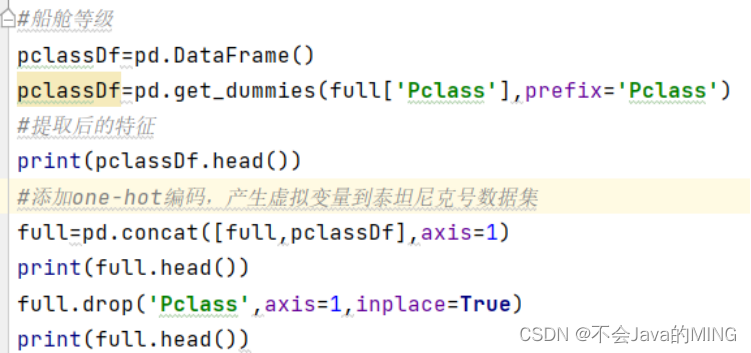

3，没有直接类别的字符串类型：

Name（乘客姓名）：

由于名字之间的头衔有着明显的区别，名字之中包含着具体的称谓，可以将称谓提取出来作为变量，可能就是不同等级有着不同的称谓，比如，结婚的人是一种，普通的人又是一种。

从姓名中获取头衔进行one-hot编码：

# 姓名
def getTitle(name):# 移除字符str1 = name.split(',')[1]str2 = str1.split('.')[0]str3 = str2.strip()return str3
titleDf = pd.DataFrame()
titleDf['Title'] = full['Name'].map(getTitle)
# print(titleDf.head())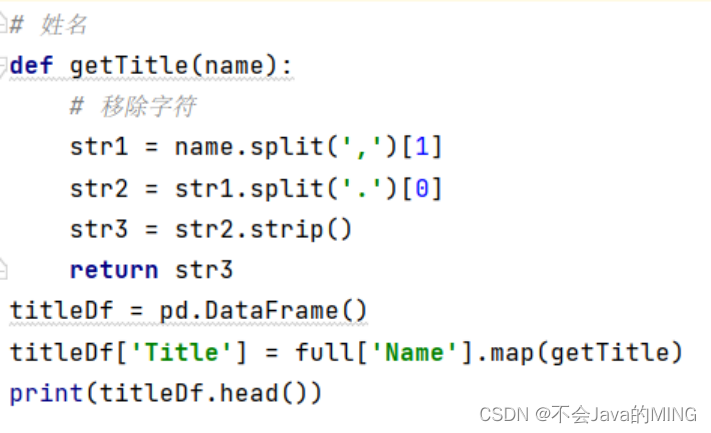

结果如图所示：

 

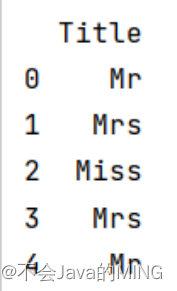
        只保留称谓，也就是可以显示不同乘客的身份，身份对于是否存活也有着很大的影响。 

        对于这些称谓，Mr已婚男人，Mrs已婚妇女，Miss年轻未婚女子等，将这些称谓统计下来：

title_mapDict = {"Capt": "Officer","Col": "Officer","Major": "Officer","Jonkheer": "Royalty","Don": "Royalty","Sir": "Royalty","Dr": "Officer","Rev": "Officer","the Countess": "Royalty","Dona": "Royalty","Mme": "Mrs","Mlle": "Miss","Ms": "Mrs","Mr": "Mr","Mrs": "Mrs","Miss": "Miss","Master": "Master","Lady": "Royalty"
}
titleDf['Title'] = titleDf['Title'].map(title_mapDict)
titleDf = pd.get_dummies(titleDf['Title'])
# print(titleDf)

Cabin（客舱号）：

处理方式和Name类似，从客舱号中提取客舱类别并进行one-hot编码：

# 客舱号
# print(full['Cabin'])
# 提取首字母
full['Cabin'] = full['Cabin'].map(lambda c: c[0])
# 进行one-hot编码
cabinDf = pd.get_dummies(full['Cabin'], prefix='Cabin')
# 添加one-hot编码产生的虚拟变量到数据集full
full = pd.concat([full, cabinDf], axis=1)
# 删掉客舱号这一列
full.drop('Cabin', axis=1, inplace=True)
familyDf = pd.DataFrame()
# print(cabinDf)

Parch（同代直系亲属），SibSp（不同代直系亲属）：

Parch+SibSp+1（乘客自己）=家庭人数

        由于并不知道最后具体到每个人的生存概率和家庭成员人数之间到底有着怎样的关系，所以要将其量化，变成方便预测的形式，于是，根据题意来依据家庭人数建立家庭类别，代码如下所示：

小家庭：家庭人数=1；

中家庭：1<家庭人数<=4

大家庭：家庭人数>=5

# Parch+SibSp
familyDf = pd.DataFrame()
familyDf['FamilySize'] = full['Parch'] + full['SibSp'] + 1
familyDf['Family_Single'] = familyDf['FamilySize'].map(lambda s: 1 if s == 1 else 0)
familyDf['Family_Small'] = familyDf['FamilySize'].map(lambda s: 1 if 2 <= s <= 4 else 0)
familyDf['Family_Large'] = familyDf['FamilySize'].map(lambda s: 1 if 5 <= s else 0)
# print(familyDf)

（还可以对年龄之类的进行分析，完善）

特征选择

主要为以下几个步骤：

• 计算特征之间的相关系数。使用皮尔逊相关系数，将每个特征与目标变量之间的相关性进行计算并量化。
• 筛选相关性强的特征。将相关系数绝对值较大的特征作为最终的特征集，可以人工设定一个阈值，只选择那些相关系数超过该阈值的特征，也可以选择前n个相关性最强的特征。
• 检查特征之间的共线性。如果多个特征之间存在高度相关的情况，则考虑删除其中某些特征，避免重复建模。

# 特征选择
# 相关系数计算特征数
full = pd.concat([full, familyDf], axis=1)
full.drop('FamilySize', axis=1, inplace=True)
corrDf = full.corr()
# print(corrDf)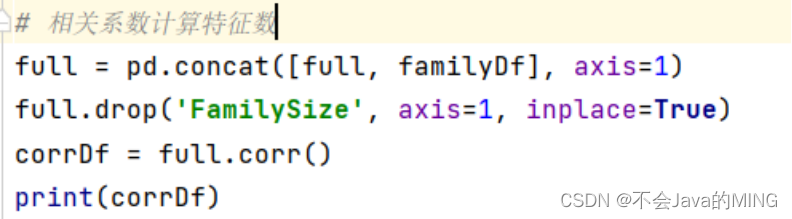

提取特征：对矩阵Survied一列输出：

# 提取Survived这一列的输出print(corrDf['Survived'].sort_values(ascending=False))

        存在问题：在进行特征选择时面临了问题，cabinDf（船舱号）和embarked（登船港口）这两个特征与特征Survived的相关性的没超过0.2，但是也不是没有相关性，所以在此尝试了使用与不使用这两种特征的两种情况，分别进行了实验，结果表明两种特征都要结果会好一点。

#是否包保留船舱号和登船港口
#都保留
full_X = pd.concat( [titleDf,#头衔pclassDf,#客舱等级familyDf,#家庭大小full['Fare'],#船票价格full['Sex'],#性别cabinDf,#船舱号embarkedDf,#登船港口] , axis=1 )
print(full_X)
#只留cabinDf船舱号
full_X = pd.concat( [titleDf,#头衔pclassDf,#客舱等级familyDf,#家庭大小full['Fare'],#船票价格full['Sex'],#性别cabinDf,#船舱号] , axis=1 )
print(full_X)
# #只留embarkedDf,登船港口
full_X = pd.concat( [titleDf,#头衔pclassDf,#客舱等级familyDf,#家庭大小full['Fare'],#船票价格full['Sex'],#性别embarkedDf,#登船港口] , axis=1 )
print(full_X)
# #两个都不要
full_X = pd.concat( [titleDf,#头衔pclassDf,#客舱等级familyDf,#家庭大小full['Fare'],#船票价格full['Sex']#性别] , axis=1 )
print(full_X)

生还率预测说明

        首先，性别是一个重要的因素。在泰坦尼克号的灾难中，女性更容易生还，因为在当时的社会中，男性更有可能让位给女性逃生。

        其次，登船港口也可以影响生还率。在泰坦尼克号的灾难中，南安普顿和谢尔堡的乘客生还率较低，可能是因为这些港口的乘客大部分是劳工和移民，他们的经济地位和社会地位较低，没有得到足够的关注和照顾。

        然后，客舱等级也是一个重要的因素。在泰坦尼克号的灾难中，头等舱的乘客生还率最高，因为头等舱的乘客通常有更好的物质条件和更高的社会地位，能够得到更好的照顾和保护。而经济舱的乘客生还率最低，因为他们的舱位在船的下层，离逃生通道较远，很难在灾难中获得及时的救援。

        此外，姓名也可以影响生还率。由于外国人很讲究名字的前缀的，在泰坦尼克号的灾难中，称呼不同对应于不同的社会地位，比如政府官员或者王室的生还率就高于普通人。

        最后，Parch（同行的父母/孩子数量）也是一个重要的因素。在泰坦尼克号的灾难中，有许多家庭一起登船，他们在灾难中通常会互相照顾和帮助，因此他们的生还率可能会更高一些。

模型构建

建立训练数据集和测试数据集

        建立训练数据集和测试数据集，使用训练数据集来训练模型，并使用测试数据集来评估模型的性能，以确定我们的模型在未见过的数据上的泛化能力。从原始数据集之中中拆分出训练数据集和测试数据集

from sklearn.model_selection import train_test_split, GridSearchCV# 由于原数据集有891条数据，我们就从full_X中提取891条数据
sourctRow = 891
# 原数据集：特征，（减一是因为是从0开始的）
source_X = full_X.loc[0:sourctRow - 1, :]
# 原数据集：标签
source_Y = full.loc[0:sourctRow - 1, 'Survived']
# 预测数据集：特征
pred_X = full_X.loc[sourctRow:, :]
# 建立训练数据集和预测数据集
size = np.arange(0.6, 1, 0.1)
scorelist = [[], [], [], [], [], []]
for i in range(0, 4):train_X, test_X, train_Y, test_Y = train_test_split(source_X,source_Y,train_size=size[i],random_state=5)

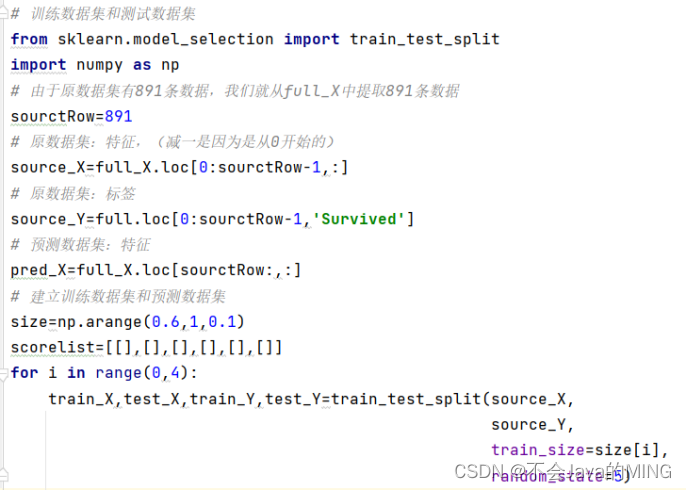
 选择不同的机器学习算法

1，逻辑回归

2，KNN

3，朴素贝叶斯

4，支持向量机

5，随机森林

6，梯度提升决策分类

训练模型，评估模型

        我们将每个不同的机器学习算法进行实现，然后对其进行评估：

具体代码如下所示：

# 逻辑回归
from sklearn.linear_model import LogisticRegression# max_iter=1000，增加迭代次数
model = LogisticRegression(max_iter=1000)
model.fit(train_X, train_Y)
scorelist[0].append(model.score(test_X, test_Y))# 随机森林
from sklearn.ensemble import RandomForestClassifiermodel = RandomForestClassifier(n_estimators=100)
model.fit(train_X, train_Y)
scorelist[1].append(model.score(test_X, test_Y))# 支持向量机Support Vector Machines
from sklearn.svm import SVCmodel = SVC()
model.fit(train_X, train_Y)
scorelist[2].append(model.score(test_X, test_Y))# 梯度提升决策分类Gradient Boosting Classifier
from sklearn.ensemble import GradientBoostingClassifiermodel = GradientBoostingClassifier()
model.fit(train_X, train_Y)
scorelist[3].append(model.score(test_X, test_Y))# KNN最邻近算法 K-nearest neighbors
from sklearn.neighbors import KNeighborsClassifiermodel = KNeighborsClassifier(n_neighbors=3)
model.fit(train_X, train_Y)
scorelist[4].append(model.score(test_X, test_Y))# 朴素贝叶斯分类 Gaussian Naive Bayes
from sklearn.naive_bayes import GaussianNBmodel = GaussianNB()
model.fit(train_X, train_Y)
scorelist[5].append(model.score(test_X, test_Y))
# score得到的是模型的正确率
print(model.score(test_X , test_Y ))

分别得到结果如下：

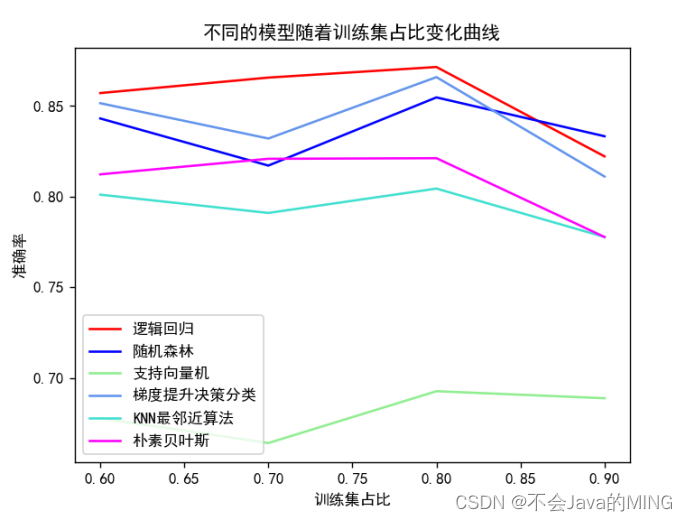
• 逻辑回归：0.8222222222222222
• 随机森林：0.8333333333333334
• 支持向量机：0.6888888888888889
• 梯度提升决策分类：0.8111111111111111
• KNN最邻近算法：0.7777777777777778
• 朴素贝叶斯分类：0.7777777777777778

将上述的模型绘制为曲线图，更加直观：

# 绘制图像
# plt.rcParams['font.sans-serif'] = 'SimHei'
# plt.rcParams['axes.unicode_minus'] = False
# color_list = ('red', 'blue', 'lightgreen', 'cornflowerblue', 'turquoise', 'magenta')
# for i in range(0, 6):
#     plt.plot(size, scorelist[i], color_list[i])
# plt.legend(['逻辑回归', '随机森林', '支持向量机', '梯度提升决策分类', 'KNN最邻近算法', '朴素贝叶斯'])
#
# plt.xlabel('训练集占比')
# plt.ylabel('准确率')
# plt.title('不同的模型随着训练集占比变化曲线')
# plt.show()

 ROC:

 方案实施

生存预测

        使用随机森林模型（这个最高），对预测数据集的生存情况进行预测：

# 使用机器学习模型，对预测数据集中的生存情况进行预测
pred_Y = model.predict(pred_X)
pred_Y = pred_Y.astype(int)
# 乘客id
passenger_id = full.loc[sourctRow:, 'PassengerId']
# 数据框：乘客id，预测生存情况的值
predDf = pd.DataFrame({'PassengerId': passenger_id,'Survived': pred_Y})# print(predDf.shape)
# print(predDf.head())
# 保存结果
predDf.to_csv('end.csv', index=False)

         生成的文件end.csv保存在附件中。

参数调优

        我们对随机森林的调优方法有很多种：

1. 调整n_estimators参数：n_estimators表示森林中树的数量。一般来说，增加树的数量可以提高模型的准确度，但也会增加模型的计算时间。可以通过交叉验证等方法来确定合适的n_estimators值。
2. 调整max_depth参数：max_depth表示树的最大深度。当max_depth过大时，模型容易出现过拟合；当max_depth过小时，模型容易出现欠拟合。可以通过交叉验证等方法来确定合适的max_depth值。
3. 调整min_samples_split参数：min_samples_split表示一个节点至少需要包含多少个样本才能被分裂。当min_samples_split过大时，模型容易出现欠拟合；当min_samples_split过小时，模型容易出现过拟合。可以通过交叉验证等方法来确定合适的min_samples_split值。
4. 调整min_samples_leaf参数：min_samples_leaf表示一个叶子节点至少需要包含多少个样本。当min_samples_leaf过大时，模型容易出现欠拟合；当min_samples_leaf过小时，模型容易出现过拟合。可以通过交叉验证等方法来确定合适的min_samples_leaf值。
5. 调整max_features参数：max_features表示在每个节点处随机选择特征的数量。当max_features过大时，模型容易出现过拟合；当max_features过小时，模型容易出现欠拟合。可以通过交叉验证等方法来确定合适的max_features值。

        我们将调整max_depth参数，min_samples_split参数，min_samples_leaf参数，max_features参数，来优化模型

# 随机森林-确定最优
model = RandomForestClassifier(n_estimators=100)
# 定义参数搜索范围
param_grid = {'max_depth': [5, 10, 15],'min_samples_split': [2, 5, 10],'min_samples_leaf': [1, 2, 4],'max_features': ['sqrt', 'log2']
}
# 使用GridSearchCV进行参数搜索
grid_search = GridSearchCV(model, param_grid=param_grid, cv=5)
grid_search.fit(train_X, train_Y)# 输出最佳参数和最佳分数
print("Best parameters: ", grid_search.best_params_)
print("Best score: ", grid_search.best_score_)# 使用最佳参数构建随机森林模型
best_model = RandomForestClassifier(n_estimators=100, **grid_search.best_params_)
best_model.fit(train_X, train_Y)
scorelist[1].append(best_model.score(test_X, test_Y))
print(best_model.score(train_X, train_Y))

         我们最终成功调优，使得结果变为0.8523274478330658，提高了准确率。

结论

        在泰坦尼克号上，女性的生还率高于男性，说明在当时的疏散过程中，女性和儿童得到了优先考虑。

        年龄也与生还率有关。儿童和老年人的生还率比其他年龄段高，从这个结果可以推测疏散时对年龄做了一定考虑，但具体原因需要更多的信息和分析。

        船级别对生还率也有影响，船票等级越高的乘客，生还率越高。

        同行的家庭成员和亲戚数量对生还率也有影响，有亲属的乘客生还率可能更高。

        乘客的登船口岸和票价等因素对生还率影响不太显著，但是这也可能是由于数据集有限的原因。

        总体来说，这些结论说明在泰坦尼克号上，逃生时有一定的优先考虑，年龄、性别、船票等级、有无亲属等因素都可能影响乘客的生还率，泰坦尼克号沉船幸存者多为老人、小孩和妇女，而牺牲者多为年轻的男士，这样的历史数据，让我感受到了人性之美与善。通过这些结论，可以更好地了解当时的情况和教训，同时也可以进一步应用于其他类似的问题和场景，提高生命安全的保障。

改进方法

        机器学习对泰坦尼克号生还情况的分析提供了一些研究成果和结论。未来的研究可以从以下几个方面进行：

        加入更多数据和特征：目前使用的数据仅包含部分乘客的信息，未来可以寻找更多相关的数据，例如那些没有生还的乘客信息、关于乘客的职业等信息。也可以考虑加入更多有影响的特征，例如在船上的位置、能否互相联络等。

        对于缺失值的处理：机器学习算法对于缺失值的处理可能影响研究结果的准确性，未来可以探索更多的方法来处理缺失值，例如使用插值方法填补缺失值。

        对算法的比较和优化：机器学习算法有很多，未来可以对不同的算法进行比较和优化，以找到更适合该问题的算法。也可以探究基于集成学习、深度学习和强化学习的算法在该问题上的拓展应用。

        进行预测：已有的数据集提供了分析泰坦尼克号事件的机会，但未来也可以尝试进行预测，例如在类似情况下，哪些乘客更有可能生还、如何制定更好的疏散计划等等。

        总体来说，研究机器学习对泰坦尼克号生还情况的分析不仅可以提供对历史事件的认知，更重要的是可以借此为未来的教育、预警和应对提供经验和启示。