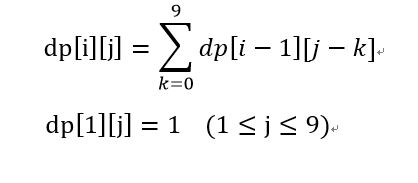51Nod_1043 幸运号码【数位DP】

                                        51Nod_1043 幸运号码

                              http://www.51nod.com/Challenge/Problem.html#!#problemId=1043

题目

1个长度为2N的数，如果左边N个数的和 = 右边N个数的和，那么就是一个幸运号码。例如：99、1230、123312是幸运号码。给出一个N，求长度为2N的幸运号码的数量。由于数量很大，输出数量 Mod 10^9 + 7的结果即可。

输入

输入N(1<= N <= 1000)

输出

输出幸运号码的数量 Mod 10^9 + 7

样例输入

1

样例输出

9

分析

dp[i][j]表示长度为i、和为j的数字串的个数（包含有前导零的情况）。长度为i的数字串是由长度为i-1的数字串再增加一个数字（0~9）形成的，因此状态转移方程为

在求长度为2N的幸运号码的数量，左边长度为N的数字串不能有前导0，因此要去掉有前导0的次数dp[N-1][j]，即dp[N][j]-dp[N-1][j]。因此长度为2N，和为j的幸运号码的数量=左部等于j的数量*右部等于j的数量=(dp[N][j]-dp[N-1][j])*(dp[N][j])，其中j的取值为1到9*N。要考虑到dp[1][0]=1,对应的幸运号码为00，由于有前导0，因此要去除，所以要将dp[0][0]设置为1。

C++程序

#include<iostream>using namespace std;typedef long long ll;const ll mod=1000000000+7;
const int N=9000;
ll dp[2][N+1];int main()
{int n;cin>>n;dp[0][0]=1;//1的特判for(int i=0;i<=9;i++)dp[1][i]=1;for(int i=2;i<=n;i++)for(int j=0;j<=i*9;j++){int len=min(j,9);ll sum=0;for(int k=0;k<=len;k++)sum=(sum+dp[(i-1)&1][j-k])%mod;dp[i&1][j]=sum;}ll ans=0;for(int i=1;i<=9*n;i++)ans=(ans+((dp[n&1][i]-dp[(n-1)&1][i])*dp[n&1][i])%mod)%mod; cout<<ans<<endl;
}