【论文笔记】cycleGAN：《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》

本文是 cycleGAN 论文《Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks》的阅读笔记。

论文一上来就给出了该图，从图中可以看到 cycleGAN 可以从源域图像转换为目标域的图像，并保留源域图像的细节，还可以从目标域图像转换回源域图像。

一、摘要

cycleGAN 的主要贡献是在不适用配对的图像对（paired images）数据时，用 GAN 实现了图像到图像的转换（image-to-image translation），即学习从源域图像到目标域图像之间的映射关系。此外除了传统的对抗损失（adversarial loss），还加入了循环一致性损失（cycle consistency loss）来保证转换后的图像保留原图像的细节信息。

二、记号

• $X$：源域图像集合
• $Y$：目标域图像集合
• $x$：一幅源域图像
• $y$：一幅目标域图像
• $\hat{x}$：生成的源域图像
• $\hat{y}$：生成的目标域图像
• $G$：从源域图像到目标域图像的生成器
• $F$：从目标域图像到源域图像的生成器
• $D_X$：判别生成的源域图像是否为真的判别器
• $D_Y$：判别生成的目标域图像是否为真的判别器

三、网络结构

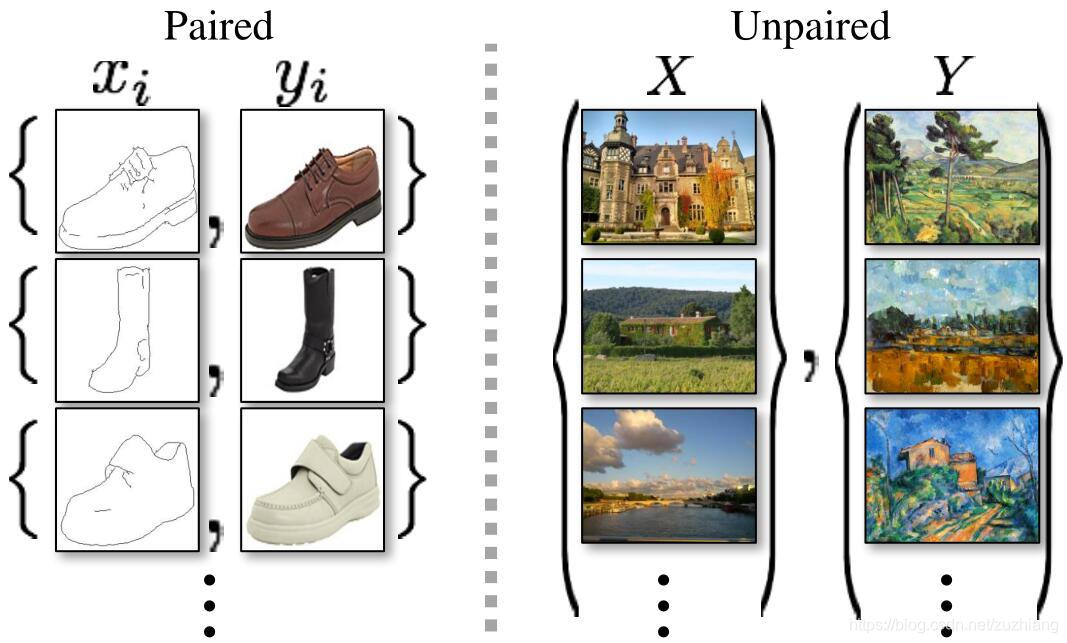
上图是配对的图像和不配对的图像的对比图。

配对的图像对举个例子就是给定一副莫奈的画作，如果再给定与该画作对应的真实场景，则图像就是配对的。这样的数据的获取是十分困难且昂贵的。所以本文没有使用配对的图像对，而是先从源域图像转化为目标域图像，只保证风格相似，而不保证内容和原图一致，记作 $\hat{y}=G(x)$。还是拿莫奈的画作举例，先将这幅画转化成看起来真实的图像，但是转换后的内容可能和画作不一致。很明显，如果只有上述操作则存在一定的问题：一是不能保证从源域图像 $x$ 生成目标域图像 $\hat{y}$ 是有意义的，因为有多种生成器 $G$ 可以让 $x$ 可以映射到 $\hat{y}$，因为 $\hat{y}$ 只要符合目标域对应的分布就可以了。此外还存在 GAN 难以训练的问题，由于模型崩溃（mode collapse）问题的存在，即生成器宁可多生成一些重复但是很“安全”的样本，也不愿意去生成多样性的样本。

上图是加入循环一致性之后两个生成器的输出示意图。

为解决上述问题，有必要在整体的网络结构上做些补充、调整，也就是实现循环一致性。举例来说，在语言翻译时，先将英语转化为法语，然后再将法语转化为英语，我们对转换前后的两个英语做损失就可以保证整个过程照着我们期望的方向进行了。所以再加一个从目标域图像转化为源域图像的生成器 $F$，先用 $G$ 将源域图像 $x$ 转化为目标域图像 $\hat{y}$，再用 $F$ 将其转化回源域图像 $\hat{x}$，然后计算 $x$ 和 $\hat{x}$ 之间的循环一致性损失，以保证 $F(G(x))\approx x$。类似的，也对目标域图像做类似的操作，以保证 $G(F(y))\approx y$。

因为有两个生成器，相应的判别器也有两个，一个是判别生成源域图像 $F(y)$ 和真实的源域图像 $x$ 是否相似的判别器 $D_X$，另一个是判别生成的目标域图像 $G(x)$ 和真实的目标域图像 $y$ 是否相似的判别器 $D_Y$。

上图是整个网络的结构示意图，(a) 图是两个生成器和两个判别器的示意图，(b) 图是前向循环一致性示意图，© 是后向循环一致性示意图。

四、损失函数

整个网络的损失函数主要包括两个，一个是对抗损失，用来将生成图像的分布与目标域图像的分布做匹配；另一个是循环一致性损失，用来防止 $G$ 和 $F$ 学到的映射互相矛盾。

对抗损失

对抗损失的公式如下：
$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}\left(G,D_Y,X,Y\right)& ={\mathbb{E}}_{y\sim p_{\text{data }}(y)}\left[\log D_Y(y)\right]\\ & +{\mathbb{E}}_{x\sim p_{\text{data }}(x)}[\log \left(1-D_Y(G(x))\right]\end{array}$$
其中 $p_{data}(x)$ 是源域图像的分布，$p_{data}(y)$ 是目标域图像的分布。类似的可以得到 ${\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}\left(F,D_X,Y,X\right)$ 的表达式。

循环一致性损失

单独的对抗损失不能保证学习到的函数可以将输入的 $x$ 映射到想要得到的输出 $y$，所以又加入了循环一致性损失，来保证 $x\to G(x)\to F(G(x))\approx x$ 及 $y\to F(y)\to G(F(y))\approx y$，其公式如下：
$$\begin{array}{rl}{\mathcal{L}}_{\text{cyc }}(G,F)& ={\mathbb{E}}_{x\sim p_{\text{data }}(x)}\left[\Vert F(G(x))-x{\Vert }_1\right]\\ & +{\mathbb{E}}_{y\sim p_{\text{data }}(y)}\left[\Vert G(F(y))-y{\Vert }_1\right]\end{array}$$

如此一来，整个网络的总损失函数为：
$$\begin{array}{rl}\mathcal{L}\left(G,F,D_X,D_Y\right)& ={\mathcal{L}}_{\text{GAN }}\left(G,D_Y,X,Y\right)\\ & +{\mathcal{L}}_{\text{GAN }}\left(F,D_X,Y,X\right)\\ & +\lambda {\mathcal{L}}_{\text{cyc }}(G,F)\end{array}$$
其中 $\lambda$ 是控制对抗损失和循环一致性损失两者重要性比重的参数，在实验中 $\lambda =10$。然后我们就可以通过最大最小化上述损失函数来得到最优的生成器了：
$$G^{\ast },F^{\ast }=\arg \underset{G,F}{\min }\underset{D_x,D_Y}{\max }\mathcal{L}\left(G,F,D_X,D_Y\right)$$

五、其他设置

• 在对抗损失中使用了最小二乘损失来代替上面的负的对数似然损失，这样可以使训练更稳定，并且输出结果更好。具体的，通过最小化以下损失来训练生成器 $G$：

$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}\left(G,D_Y,X,Y\right)& ={\mathbb{E}}_{x\sim p_{\text{data }}(x)}[(D(G(x))-1{)}^2]\end{array}$$

​ 通过最小化以下损失来训练判别器 $D$：
$$\begin{array}{rl}{\mathcal{L}}_{\mathrm{G}\mathrm{A}\mathrm{N}}\left(G,D_Y,X,Y\right)& ={\mathbb{E}}_{y\sim p_{\text{data }}(y)}\left[(D(y)-1{)}^2\right]+{\mathbb{E}}_{x\sim p_{\text{data }}(x)}[D(G(x){)}^2]\end{array}$$

• 为了减少模型的震荡，不适用最新的生成器产生的图像作为判别器的输入来训练判别器，而是使用生成器的历史输出来训练判别器。具体的，设置了一个缓冲池保存生成器生成的50张最新图像。
• 使用 Adam 优化器，batch size 为 1，学习率为 2e-4，在前100个 epoch 里保持不变，在之后的100个 epoch 里线性衰减到0。