PTA(02)典例详解（11，18，20，21，22） 7-11 Cassels方程 7-18 找出三位水仙花数 7-20 洛希极限7-21 胎压监测 7-22 前世档案

目录

 7-11 Cassels方程 

7-18 找出三位水仙花数

 7-20 洛希极限

7-21 胎压监测 

 7-22 前世档案

 7-11 Cassels方程

Cassels方程是一个在数论界产生了巨大影响的不定方程：x2+y2+z2=3xyz。该方程有无穷多自然数解。

本题并不是要你求解这个方程，只是判断给定的一组 (x,y,z) 是不是这个方程的解。

输入格式：

输入在第一行给出一个不超过 10 的正整数 N，随后 N 行，每行给出 3 个正整数 0<x≤y≤z≤1000。

输出格式：

对于每一组输入，如果是一组解，就在一行中输出 Yes，否则输出 No。

输入样例：

2
1 1 1
5 6 7

输出样例：

Yes
No

 解题思路：将输入的x，y，z存入数组进行判断，通过下标递增使其进行下一个判断，代码如下

#include<stdio.h>
void main()
{int x[100],y[100],z[100],n,i,m,p;scanf("%d\n",&n);for(i=0;i<n;i++)scanf("%d %d %d\n",&x[i],&y[i],&z[i]);for(i=0;i<n;i++);{m=x[i]*x[i]+y[i]*y[i]+z[i]*z[i];p=3*x[i]*y[i]*z[i];if(p==m)printf("Yes\n");elseprintf("No\n");return 0;}
}

 7-18 找出三位水仙花数

 

本题要求编写程序，输出给定正整数M和N区间内的所有三位水仙花数。三位水仙花数，即其个位、十位、百位数字的立方和等于该数本身。

输入格式:

输入在一行中给出两个正整数M和N（100≤M≤N≤999）。

输出格式:

顺序输出M和N区间内所有三位水仙花数，每一行输出一个数。若该区间内没有三位水仙花数，则无输出。

如果M或者N不符合题目的要求，则输出Invalid Value.。

输入样例1:

100 400

输出样例1:

153
370
371

输入样例2:

500 600

输出样例2:

输入样例3：

990 101

输出样例3：

Invalid Value.

 解题思路：首先使输入的M,N满足（100≤M≤N≤999），使用逻辑运算，而后分解出每一位数使其得到立方和判断是否等于这个数本身，代码如下

#include <stdio.h>
#include <math.h>
int main( )
{ int a,b,c,M,N,i,j;scanf("%d %d",&M,&N);i=M;j=N;if(M<=N&&M>=100&&N<=999){	for(i;i<=j;i++){a=i/100;b=i%100/10;c=i%10;if(i==a*a*a+b*b*b+c*c*c){printf("%d\n",i);}}
}else{printf("Invalid Value.\n");}return 0;
}

 7-20 洛希极限

洛希极限（Roche limit）是一个天体自身的引力与第二个天体造成的潮汐力相等时的距离。当两个天体的距离少于洛希极限，天体就会倾向碎散，继而成为第二个天体的环。它以首位计算这个极限的人爱德华·洛希命名。（摘自百度百科）

大天体密度与小天体的密度的比值开 3 次方后，再乘以大天体的半径以及一个倍数（流体对应的倍数是 2.455，刚体对应的倍数是 1.26），就是洛希极限的值。例如木星与地球的密度比值开 3 次方是 0.622，如果假设地球是流体，那么洛希极限就是 0.622×2.455=1.52701 倍木星半径；但地球是刚体，对应的洛希极限是 0.622×1.26=0.78372 倍木星半径，这个距离比木星半径小，即只有当地球位于木星内部的时候才会被撕碎，换言之，就是地球不可能被撕碎。

本题就请你判断一个小天体会不会被一个大天体撕碎。

输入格式：

输入在一行中给出 3 个数字，依次为：大天体密度与小天体的密度的比值开 3 次方后计算出的值（≤1）、小天体的属性（0 表示流体、1 表示刚体）、两个天体的距离与大天体半径的比值（>1 但不超过 10）。

输出格式：

在一行中首先输出小天体的洛希极限与大天体半径的比值（输出小数点后2位）；随后空一格；最后输出 ^_^ 如果小天体不会被撕碎，否则输出 T_T。

输入样例 1：

0.622 0 1.4

输出样例 1：

1.53 T_T

输入样例 2：

0.622 1 1.4

输出样例 2：

0.78 ^_^

首先先解读一下题目吧，题目比较长而且专业名词较多 但是仔细看给我们的输入格式，多读几次题目就知道在过程中只需考虑流体和刚体，注意我们要算的并不是洛希极限，而是洛希极限与大天体半径的比值，随后只需要用这个比值和两个天体的距离与大天体半径的比值相比较，化解就是题目中所说的意思，也就是两个天体的距离与洛希极限比较，从而得出会不会被撕碎，在理解题目后就是非常简单的，代码如下

#include<stdio.h>
int main()
{int a;float n,m,p;scanf("%f %d %f",&n,&a,&m);if(a==0)p=n*2.455;elsep=n*1.26;if(p>m)printf("%.2f T_T",p);elseprintf("%.2f ^_^",p);return 0;	
} 

7-21 胎压监测 

 小轿车中有一个系统随时监测四个车轮的胎压，如果四轮胎压不是很平衡，则可能对行车造成严重的影响。

让我们把四个车轮 —— 左前轮、右前轮、右后轮、左后轮 —— 顺次编号为 1、2、3、4。本题就请你编写一个监测程序，随时监测四轮的胎压，并给出正确的报警信息。报警规则如下：

• 如果所有轮胎的压力值与它们中的最大值误差在一个给定阈值内，并且都不低于系统设定的最低报警胎压，则说明情况正常，不报警；
• 如果存在一个轮胎的压力值与它们中的最大值误差超过了阈值，或者低于系统设定的最低报警胎压，则不仅要报警，而且要给出可能漏气的轮胎的准确位置；
• 如果存在两个或两个以上轮胎的压力值与它们中的最大值误差超过了阈值，或者低于系统设定的最低报警胎压，则报警要求检查所有轮胎。

输入格式：

输入在一行中给出 6 个 [0, 400] 范围内的整数，依次为 1~4 号轮胎的胎压、最低报警胎压、以及胎压差的阈值。

输出格式：

根据输入的胎压值给出对应信息：

• 如果不用报警，输出 Normal；
• 如果有一个轮胎需要报警，输出 Warning: please check #X!，其中 X 是出问题的轮胎的编号；
• 如果需要检查所有轮胎，输出 Warning: please check all the tires!。

输入样例 1：

242 251 231 248 230 20

输出样例 1：

Normal

输入样例 2：

242 251 232 248 230 10

输出样例 2：

Warning: please check #3!

输入样例 3：

240 251 232 248 240 10

输出样例 3：

Warning: please check all the tires!

解题思路：将四个轮胎的胎压存入数组并选出最大值，止呕根据有提议进行比较，使用最大值减去每个轮胎的胎压与阈值比较，同时使每个轮胎的胎压与最小值比较，要注意这里的逻辑关系是或，对有问题的轮胎进行计数，代码如下：

#include<stdio.h>
int main()
{int a[4],Max=0,luntai,min,fanwei,b=0;for(int i=0;i<4;i++){scanf("%d",&a[i]);if(a[i]>Max)Max=a[i];}scanf("%d %d",&min,&fanwei);for(int i=0;i<4;i++){if(Max-a[i]>fanwei||a[i]<min){b++;luntai=i;}}if(b==0){printf("Normal");}else if(b==1){printf("Warning: please check #%d!",luntai+1);}else{printf("Warning: please check all the tires!");}
}

 7-22 前世档案

网络世界中时常会遇到这类滑稽的算命小程序，实现原理很简单，随便设计几个问题，根据玩家对每个问题的回答选择一条判断树中的路径（如下图所示），结论就是路径终点对应的那个结点。 

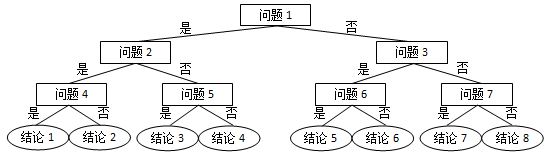
现在我们把结论从左到右顺序编号，编号从 1 开始。这里假设回答都是简单的“是”或“否”，又假设回答“是”对应向左的路径，回答“否”对应向右的路径。给定玩家的一系列回答，请你返回其得到的结论的编号。

输入格式：

输入第一行给出两个正整数：N（≤30）为玩家做一次测试要回答的问题数量；M（≤100）为玩家人数。

随后 M 行，每行顺次给出玩家的 N 个回答。这里用 y 代表“是”，用 n 代表“否”。

输出格式：

对每个玩家，在一行中输出其对应的结论的编号。

输入样例：

3 4
yny
nyy
nyn
yyn

输出样例：

3
5
6
2

 

 这里要使用到一个gather函数，详细用法可见大佬的http://t.csdn.cn/flFIz，通过读入字符只判断是否为n再使用算法计数并输出，使程序简单化了很多，代码如下

#include <stdio.h>
#include <math.h>
int main()
{// inputint n, m; scanf("%d%d", &n, &m);for (int i=0; i<m; i++){getchar();int sum = 1;for (int j=0; j<n; j++){char ch = getchar();if (ch == 'n')sum += pow(2, n-1-j); }// outputprintf("%d\n", sum);}return 0;
}