代码随想录打卡第五十六天|1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和

本文主要是介绍代码随想录打卡第五十六天|1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1143.最长公共子序列

题目： 给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。
一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。
两个字符串的公共子序列是这两个字符串所共同拥有的子序列。
在这里插入图片描述
题目链接： 1143.最长公共子序列
如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;
如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

class Solution {public int longestCommonSubsequence(String text1, String text2) {//定义一个二维dp 数组//dp[i][j] 表示A[:i-1] B[:j-1]的最长公共子序列int dp[][] = new int[text1.length()+1][text2.length()+1];for(int i=1;i<=text1.length();i++){for(int j=1;j<=text2.length();j++){if(text1.charAt(i-1)==text2.charAt(j-1)){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);}}}return dp[text1.length()][text2.length()];}
}

1035.不相交的线

题目：
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：
nums1[i] == nums2[j]
且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。
以这种方法绘制线条，并返回可以绘制的最大连线数。
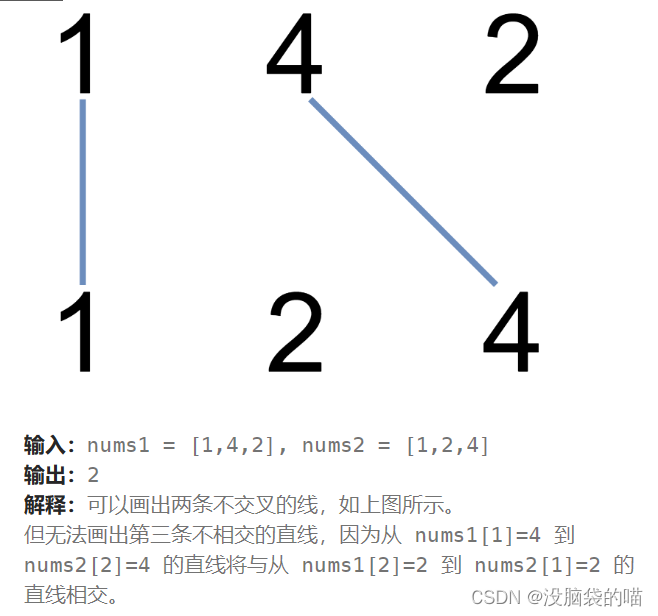
在这里插入图片描述

题目链接： 1035.不相交的线

其实就是上一题的变形但题目描述的很巧妙

class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int dp[][] = new int[nums1.length+1][nums2.length+1];for(int i=1;i<=nums1.length;i++){for(int j=1;j<=nums2.length;j++){if(nums1[i-1]==nums2[j-1]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=Math.max(dp[i][j-1],dp[i-1][j]);}}}return dp[nums1.length][nums2.length];}
}