有根树的表达——树结构的建立

树结构是一种数据结构，它由结点，以及连接结点的边构成。

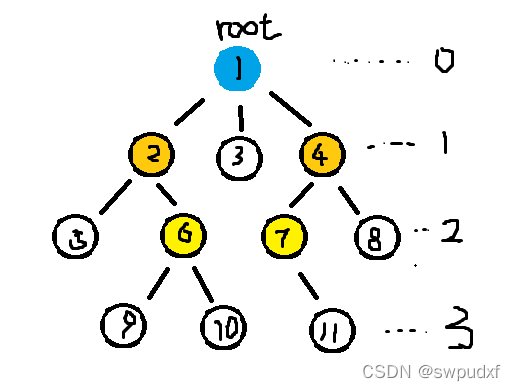
图中的圆圈表示节点，线表示边。若图中有一个名为“根”的特殊节点，那么这颗树可以被可以称为有根树。

树中节点与节点之间具有父子关系，图中由边连接着的两个节点1与节点2中节点1被称作为节点2的父节点，节点2为节点1的子节点，节点1与3，节点1与4同样具有父子关系。图中有一个节点没有父节点该结点被称为根，图中蓝色结点1就为根。同时我们引入左子右兄弟概念，如图结点2，3，4同时与节点1连接 节点2为节点1的左子节点 节点3为节点2的右兄弟节点 节点4为节点3的右兄弟节点 如节点2又连接着节点5，6 那么节点5是节点2的左子节点，节点6是节点5的右兄弟节点。 既然为被称作树结构那么没有子节点的节点被称为叶节点 图中白色节点则为叶节点，黄色节点为中间节点，蓝节点为根节点

图中某个节点具有的子节点数为该节点的度，如图中的节点1的度为3，节点2的度为2.

从根到节点x的路径长度成为x的深度，如图中2，3，4的深度都为2，图中5，6，7，8为2。另外节点x到叶节点的最大路径长度也被成为节点x的高，如图中节点8，10，5，3的高为0，节点6，7的高为1，节点2，4的高为2。

有根树的表达：（此例题来源于会津大学oj题目）

若对一个有根树的要求如下：

输入：第一行输入节点的个数n，接下来的n行按照下述格式输入各节点的信息，每个节点占一行。

id,k,c1,c2,c3....ck;(id为节点的编号,k为度,c1,c2,c3...ck为第一个子节点到第k个子节点的编号)

输出：按照下述格式输出节点的信息。节点信息

按照编号升序排列。

node id:  parent = p, depth = d, type, [c1,c2,c3.....ck]

p代表父节点编号。不存在父节点时输出-1。d表示节点的深度。type表示节点的类型，从root（根），internal node（内部节点），leaf，三个字符串中选择其一。c1,c2...ck是子节点列表。这里我们将给定树视作有序树，按照输入的顺序输出。相邻的信息用逗号和空格隔开。

限制：1 <=n<=100000。

输入示例：

13
0 3 1 4 10
1 2 2 3
2 0
3 0
4 3 5 6 7
5 0
6 0
7 2 8 9
8 0
9 0
10 2 11 12
11 0
12 0

输出示例：

node 0: parent = -1, depth = 0, root, [1, 4, 10]
node 1: parent = 0, depth = 1, internal node, [2, 3]
node 2: parent = 1, depth = 2, leaf, []
node 3: parent = 1, depth = 2, leaf, []
node 4: parent = 0, depth = 1, internal node, [5, 6, 7]
node 5: parent = 4, depth = 2, leaf, []
node 6: parent = 4, depth = 2, leaf, []
node 7: parent = 4, depth = 2, internal node, [8, 9]
node 8: parent = 7, depth = 3, leaf, []
node 9: parent = 7, depth = 3, leaf, []
node 10: parent = 0, depth = 1, internal node, [11, 12]
node 11: parent = 10, depth = 2, leaf, []
node 12: parent = 10, depth = 2, leaf, []

那么该有根树如下图所示

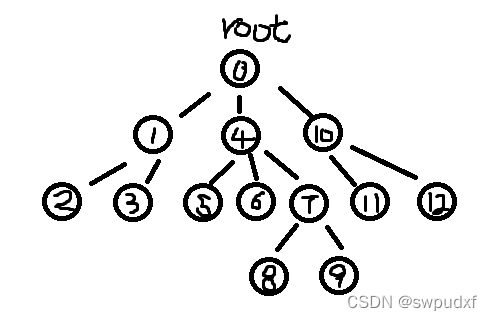
 代码如下：

#include<bits/stdc++.h>using namespace std;int dep[100005]={0};struct pp{int p,l,r;
}i[100005];
//采用结构体的方法记录该节点的父节点p，左子节点l，右兄弟r；void findd(int a,int d){dep[a]=d;if(i[a].r!=-1) findd(i[a].r,d);if(i[a].l!=-1) findd(i[a].l,d+1);
}
//用递归的方法记录每个节点的深度void print(int a){cout<<"node "<<a<<": parent = "<<i[a].p<<", depth = "<<dep[a]<<", ";if(i[a].p==-1) cout<<"root, ";else if(i[a].l==-1) cout<<"leaf, ";else cout<<"internal node, ";if(i[a].l!=-1){cout<<'['<<i[a].l;int b=i[i[a].l].r;while(b!=-1){cout<<", "<<b;b=i[b].r;	}cout<<']';}else{cout<<"[]";}cout<<endl;
}int main()
{int n;cin>>n;for(int c=0;c<n;c++) i[c].l=i[c].p=i[c].r=-1;//初始化为-1，便于讨论for(int c=0;c<n;c++){int id,k,j;cin>>id>>k;for(int d=0;d<k;d++){int a;cin>>a;if(d==0) i[id].l=a;//第一个子节点为左子节点else i[j].r=a;//剩下的依次为上一节点的右兄弟节点j=a;i[a].p=id;//所有节点的父节点都是id节点}}int r;for(int c=0;c<n;c++){if(i[c].p==-1) r=c;//若某一结点没有父节点那么该节点一定是根节点}findd(r,0);//从根节点开始利用递归得到每个节点的深度for(int c=0;c<n;c++) print(c);
}

我是笨蛋