基于时间序列的加法季节模型和乘法季节模型

基于时间序列的加法季节模型和乘法季节模型以及两者之间的比较如下：

实验数据来源与1962年到1991年德国工人季度失业率序列：

一、加法季节模型

1、首先加载所需的包：

2、导入数据，并将数据转换为季节数据：

3、得到时序图如下，发现既有季节效应又有上升趋势效应：

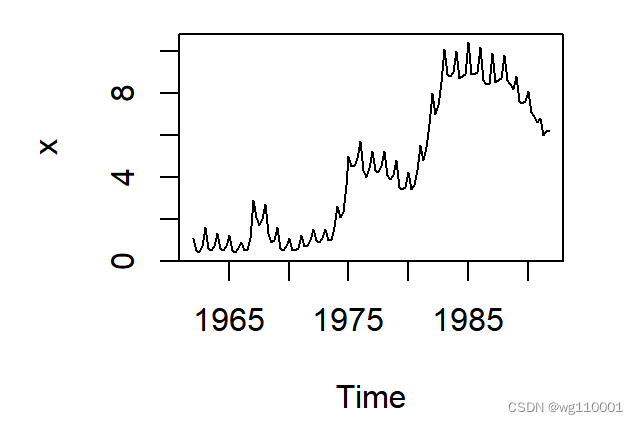
4、接着我们对数据进行一阶四部差分：

一阶四步差分时序图如下：

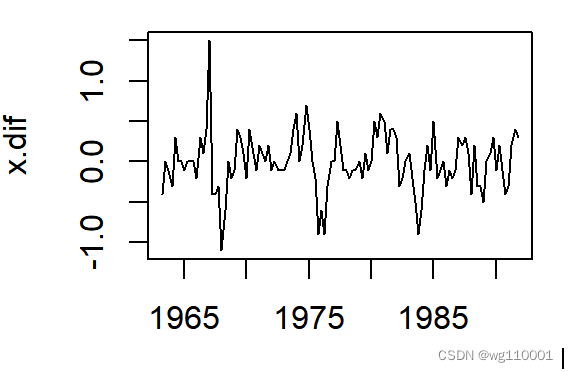
从一阶四步差分时序图可以看出，我们消除了上升趋势效应以及季节效应，即为平稳序列。

5、接着画出差分后序列相关图和偏自相关图：

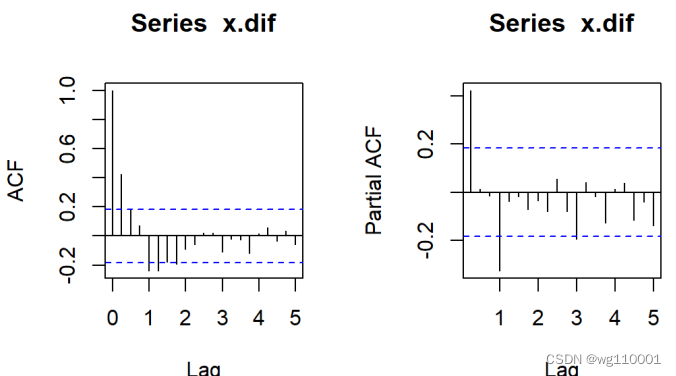
 结果显示自相关具有拖尾性，偏自相关图在一阶和3阶之后都落入两倍的标准差之内了，综合考虑，最后拟合一个假发季节模型:ARIMA((1,4),(1,4),0))

6、模型拟合结果及优化结果对比显示：

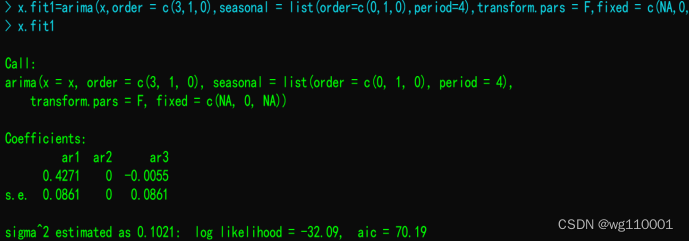  结果显示ARIMA((1,4),(1,4),0))模型aic数值较小，ARIMA((1,4),(1,4),0))模型较好。

7、运用forecast函数进行预测

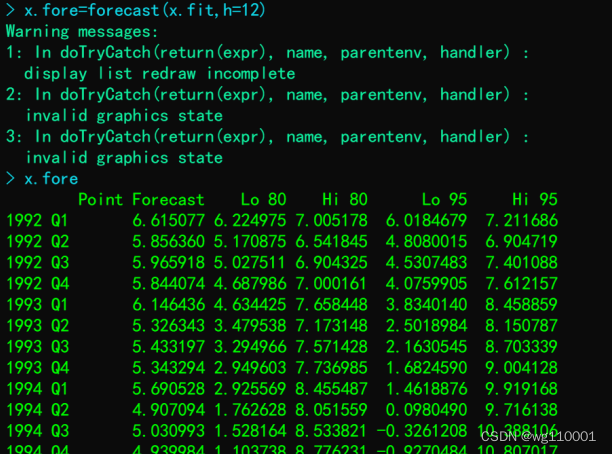
 8、预测结果可视化：

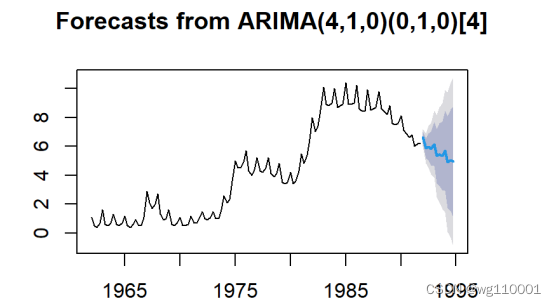
9、模型的残差序列白噪声检验：

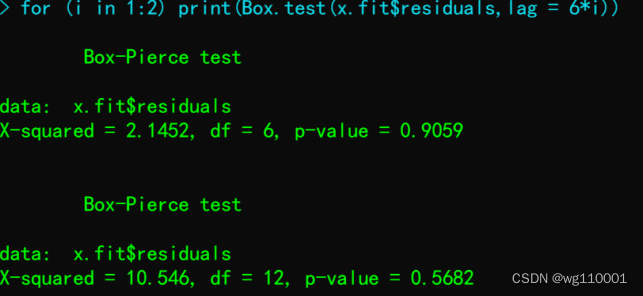
p值较大，说明加法季节模型很好的提取了数据信息，模型拟合效果很理想。

二、乘法季节模型

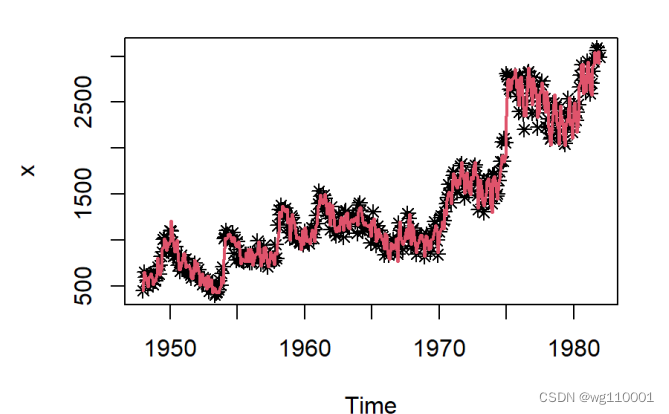
数据来源于1948年到1981年美国女性月度事业率序列

1、读取数据，并将数据转换为时间序列数据2、输出时间序列时序图，发现既有周期性又有上升趋势效应：

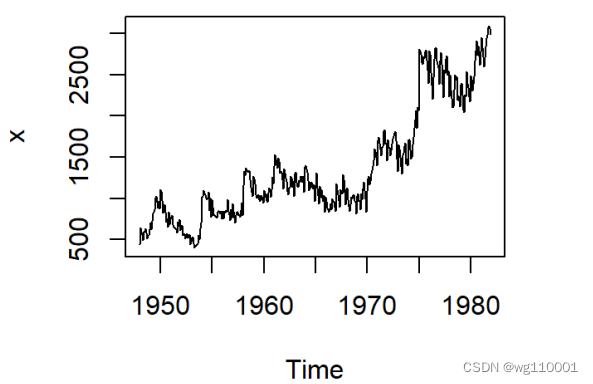
 接着我们对数据进行一阶12步差分：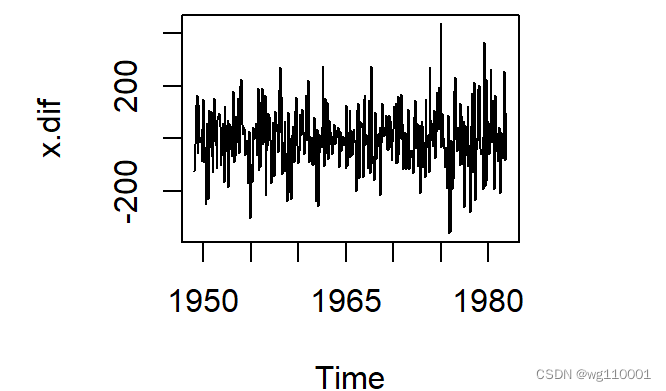

从一阶12步差分时序图可以看出，我们消除了上升趋势效应以及周期效应，即为平稳序列。

3、接着画出差分后序列相关图和偏自相关图：

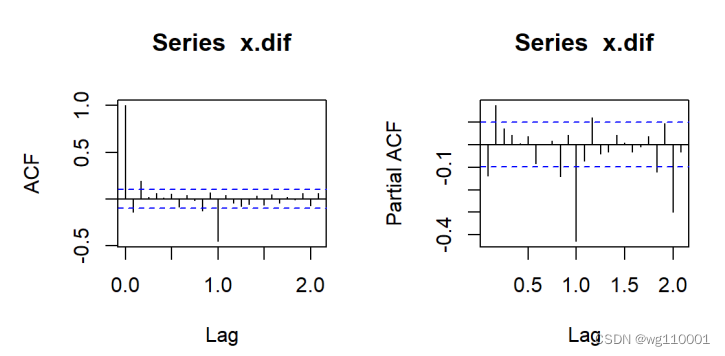
结果显示自相关和偏自相关都具有拖尾性。

4、首先拟合一个加法季节模型:ARIMA(1,12),1)

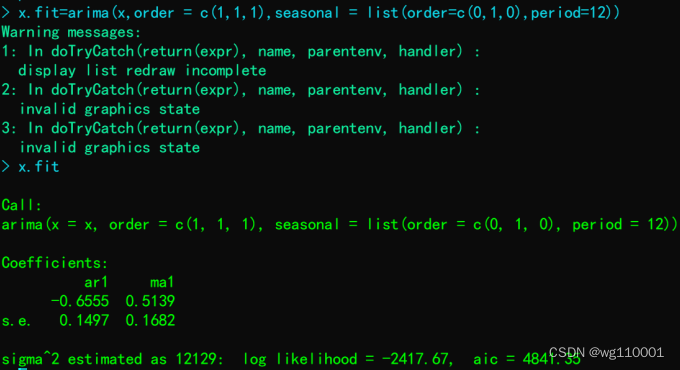
 5、模型残差序列白噪声检验：

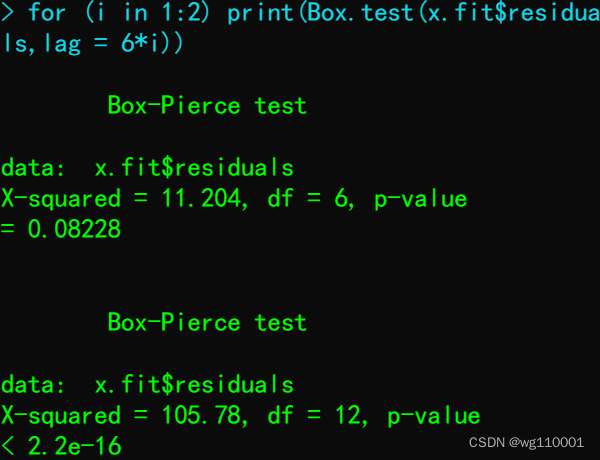
 由结果可得6阶时p值为0.08228，12阶时p值为2.2e-16,取α值为0.1时，均拒绝原假设，说明残差为非白噪声序列，说明时间序列选择加法季节效应模型不正确。

6、接着我们选择乘积季节效应进行拟合，关键在于阶数的选择，结束的选择，我们仍选择用自相关和偏自相关图来观察：

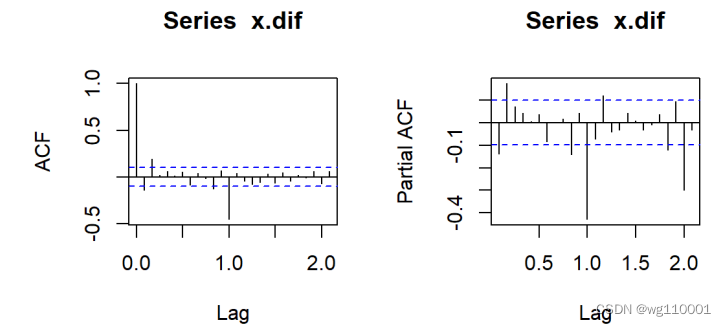
 从短期来看，自相关在短期和偏自相关都是拖尾的，自相关认为时1阶即一个周期截尾的，偏自相关系数1阶拖尾，p取0，q取1。

7、6期乘法季节序列模型预测：

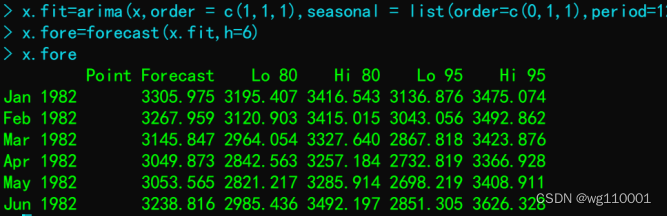
 8、结果可视化：

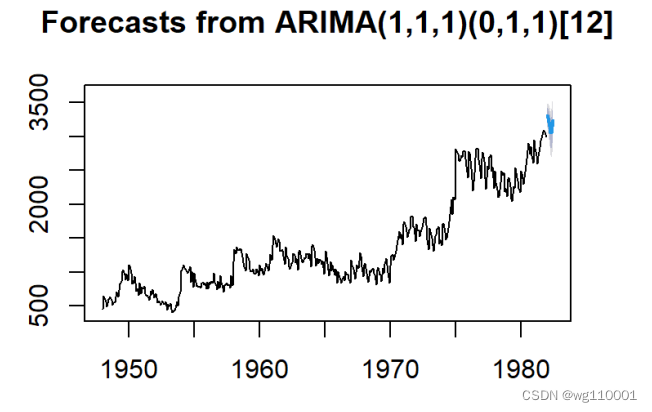
 9、模型残差序列白噪声检验：

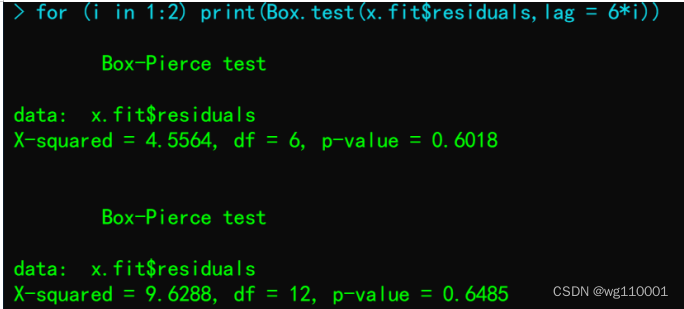
p值较大，说明乘法季节模型很好的提取了数据信息，模型拟合效果很理想。