信号完整性基础03：反射与阻抗匹配（1）

说在开头：关于“惰性气体”

英国剑桥大学当时的校长是：威廉.卡文迪许公爵，他的祖上有一位“科学怪人”：亨利.卡文迪许，他一辈子深居简出，淡泊名利，从不靠刷论文来体现自己的学术水平，留下了丰富的手稿。威廉.卡文迪许校长自己掏腰包建立了一座实验室（就是名震江湖的：卡文迪许实验室），聘请当时的电磁学宗师：麦克斯韦来执掌，这个职务相当于剑桥大学物理系的主任，麦克斯韦对亨利.卡文迪许的手稿很感兴趣，花了大量时间来整理，1879年麦克斯韦去世后，就由瑞利男爵来接班执掌了。

瑞利男爵关注到了亨利.卡文迪许手稿里记录的一件怪事：将一个玻璃容器倒扣在碱液里面，空气都聚集在顶部，伸进去两个电极，在其顶部打出电火花，空气中的氧气和氮气在电火花的作用下形成二氧化碳和二氧化氮；而二氧化碳和二氧化氮是酸性的，会被碱液中和，随着不断放电，顶部的空气越来越少，按理来说最后应该被吸收的一点不剩才对。但是卡文迪许发现，结果却并非如此：最后总有一个小气泡消除不掉。这是为什么呢？卡文迪许只是做了记录，并未下结论，100年过去了，大家都没注意到这个事情。

但是瑞利男爵注意到了，因为他当时在测量各种气体的密度，别的气体密度测量结果都很准确，唯独氮气的密度老是测不准，获得纯净氮气的方法有两个：1，将含氮的化合物里面提取出氮气；2，清除掉空气里的其它气体，那么就只剩下了氮气。用这两种方法获得的氮气测量出来的密度居然是不同的，相差了1.2‰。瑞利男爵是个爱较真的科学家，他头都大了（500斤重~），这到底是为什么呢？他一次次的比对测量，但测出来的就是对不上，所以亨利.卡文迪许的手稿给了他一个启发：嘿嘿，空气的成分肯定有问题。

瑞利男爵自己搞不定，于是广发英雄帖，看谁能过来帮他，于是叫来了一个名叫：拉姆塞的家伙，表示自己非常有兴趣，可以一起搞一搞。拉姆塞用了别的方法，他让空气不断燃烧镁粉，镁粉非常活跃，在高温下会跟氧气和氮气发生作用，最后却还总是留下个小气泡。这个气泡到底是啥玩意？量太少，测定成分也不够啊。于是拉姆塞开始没日没夜的烧镁粉，搞到了好几升这种气体（想象一下实验室的场景，何其壮观）。这下足够实验用了，他们想尽办法把这东西跟其它元素放在一起：加热、放电统统试了一遍，就是刀枪不入，跟谁都不发生反应。拉姆塞一看，这么搞也不是办法啊。要不就请出老师的法宝来吧。

拉姆塞的老师叫：基尔霍夫。大牛中的大牛啊（基尔霍夫第一、第二定律不要忘了哦），而且他还有一位好基友：本生。这个本生擅长自己发明化学仪器，搞了一个煤气灯——本生灯，温度奇高，能达到2300℃（酒精灯一般在400℃~500℃），当年本生把不同金属盐撒到本生灯上会出现五颜六色的火焰，他觉得这颜色跟金属元素有关系（比如：含Na的盐会发黄光，如下图所示；含Ga的盐会发红光），于是越烧越兴奋，逮到什么烧什么。基尔霍夫看不下去了：你这没完没了的，是在搞啥玩意啊？本生对基尔霍夫说：不同颜色很可能代表不同的元素。基尔霍夫眼前一亮：你这么看颜色不靠谱啊，你虽然看到了黄光但也不知道具体有多黄，要精确描述光的颜色，得靠光谱分析啊，来，咱哥俩好基友一起搞吧。于是他们就搭上了，基尔霍夫找来三棱镜，两个人一顿操作猛如虎，搞出来世界上第一台光谱仪。他们又一顿烧，把能烧的盐都烧了一遍，发现：钠盐的光谱是两条很窄的黄色谱线，不是连续的光谱；各种元素的谱线又都不大一样，好比每种元素有各自不同的二维码。1859年10月20日，他们向柏林科学院做了个报告，说搞清楚了太阳上的元素组成。底下一大帮科学家在纳闷，他们啥时候去的太阳啊。从此天体物理进入了新阶段，人类现在可以用光谱来分析物质的组成元素了。

拉姆塞想起老师基尔霍夫的光谱仪，但是基尔霍夫烧的是固体，气体怎么办呢？不过这也难不倒他们，他们发明了一种新办法：在气体瓶子里放电，用电场来激发气体辉光。发明这玩意的人叫：克鲁克斯，是瑞丽男爵和拉塞姆的后援，这个管就叫“克鲁克斯管”。他们观察了气体的光谱线，一看吓一跳：这种元素的光谱从来没见过啊，肯定是新元素。于是给这新元素起了个名字叫“氩”，希腊文中氩的意思是懒惰，所以惰性气体由此得名。拉塞姆一看新发现的氩元素跟哪个族的元素都不像啊，难不成是自成一派？于是再接再厉又分离出好几种惰性气体，这些气体组成了元素周期表的新一族，元素周期表又新增了一列，这说明了门捷列夫元素周期表的前瞻性和预见性。

这下一个坑变成了两个坑：1，元素的周期性到底是怎么来的；2，为什么不同元素会有不同的光谱线，而且光谱还不连续？（参考自:吴京平-无中生有的世界）

一，波的反射和折射

说起反射，在我脑海中浮现的画面是空气中一束光线射入水面，然后让我画出反射和折射的方向，以及求出反射和折射光线的强度。那为什么一束光在不同介质面会发生反射/折射呢？

我们在高中时学过光的反射和折射是可以用惠更斯原理来解释：球形波面（振动状态相同的位置，例如所有的波峰或波谷）上的每一点都是一个刺激球面波的子波源（新的波），子波的波速与频率等于初级波的波速和频率，此后这些子波在波前进方向的包络面就是新的波面。这也是光的波动性原理的解释，但惠更斯认为光是一种机械波，是机械振动形式的传递，所以我们可以用水波来想象，其波面就是我们看到的一圈圈的水波，波传递的方向（波线）与波面垂直。如果波遇到障碍物，会返回来继续传播，这种现象就是波的反射。而波的折射是由于波在不同介质中的速度不同造成的，在波的折射中，波的频率不变，波速和波长都会发生改变。

而从微观的角度来说，电磁波和物质相互作用的本质就是电磁波带动物质中电子运动，能量被其吸收，再由电子放出散射波的过程。由于波承载了电磁的全部物理意义（能量），那么最后形成的结果就应该是原入射波和散射波的叠加。

假定在一个均匀介质中有一朝z方向传播的电磁波（平面波），其与z垂直的平面代表同相位面，考虑一个波前a，它所经过的平面A上的原子，其所含电子都会因相互作用而发出新的散射波。因为他们处在同相位面上，因此他们散射出来的波在源处也是同相位的，这些子波互相叠加只能产生一个向前传播的散射波（坡印廷矢量方向）。所以，电磁波在物质中的传播，其实是无数平面上的散射子波在除了某一个方向外，其他方向处处抵消的结果。而在不同介质面的交界处，散射子波在不同方向出现了叠加不为0的情况。

我们再来具体看看这个散射波和原入射波叠加之后，会有什么效果。假定介质由原子构成，原子中的电子在电场激励下做简谐振动，那么可想而知，电子会产生位移，而且位移的大小和外加电场成正比（介质极化）；散射出的平面波正比于散射平面处的入射波，只是做了一个90度的相移，即我们可以认为入射波的强度没有发生变化，只是相位发生了延迟。相当于介质中的无限平面原子把入射光坚持不懈地拖拽，假设原来光在真空中传播z的距离，相位只落后kz，而拖拽后相位落后了nkz；即波动传播的速度降低了n倍。极化率（介电常数）决定折射率，折射率高，波动速度越慢，

传输线信号传输的本质是电磁波信号传播，但是其信号反射原理同光的反射/折射完全不同，传输线信号的反射是由于传输线阻抗的变化所导致，而非介质变化引起的。我们知道电磁波的反射会导致其部分能量的损失，所以传输线信号的反射就不可避免的同信号质量联系在一起，我们要尽量避免传输线中间的阻抗不连续点。

在上一章传输线定义中说过，传输信号的目的是：让接收端能正确的接收到信号。很明显假如信号发生了反射，那么根据能量守恒原理，入射信号的能量必然会减小，信号幅度必将发生变化（可能减小/增加，看在什么阶段）。

二，信号为什么反射

信号沿传输线传播时，路径上每点都有相应的瞬时阻抗，若瞬时阻抗发生变化（举个栗子，阻抗由原先的50Ω变成60Ω），那么部分信号将沿着与原传播方向相反的方向反射，而另外一部分将继续传播。

好，扯了辣么多，接下来我们进入正题：我们用物理规则结合数学公式来推导信号反射的原理，当信号沿着传输线从阻抗Z1进入到Z2的边界，此时必须保证在此边界处：V1=V2，I1=I2；同一点的电压和电流必须保持连续：

——为什么要相等呢？这是基老师的第一第二定律告诉我们：必须相等，不然世界大乱。

1. 如果在无穷小跨越交接处的电压不连续，那么将在交界处将产生一个无穷大的电场，毁灭宇宙；

2. 如果在此电流不连续，那么会出现一个特殊的情况，电子不会无中生有，也不会凭空消失；就算理论上会出现无中生有或凭空消失（举个栗子：量子潮汐，宇宙大爆炸之类的），那阻抗不连续出也将发生灾难。

如下图所示，既然交界处电流相等I1=I2，又有I1 = V1/Z1 ，I2 = V2/Z2；从而推导出V1/Z1 = V2/Z2，而Z1 ≠ Z2，很显然：V1=V2，I1=I2，I1 = V1/Z1 ，I2 = V2/Z2；这四个等式不能同时满足。为了防止世界被破坏，为了守护世界的和平，贯彻爱与真实的邪恶：必须在区域1中产生一个反射回源端的电压，它唯一的目的是吸收入射信号和传输信号不匹配的电压和电流（守护住了世界的和平）。

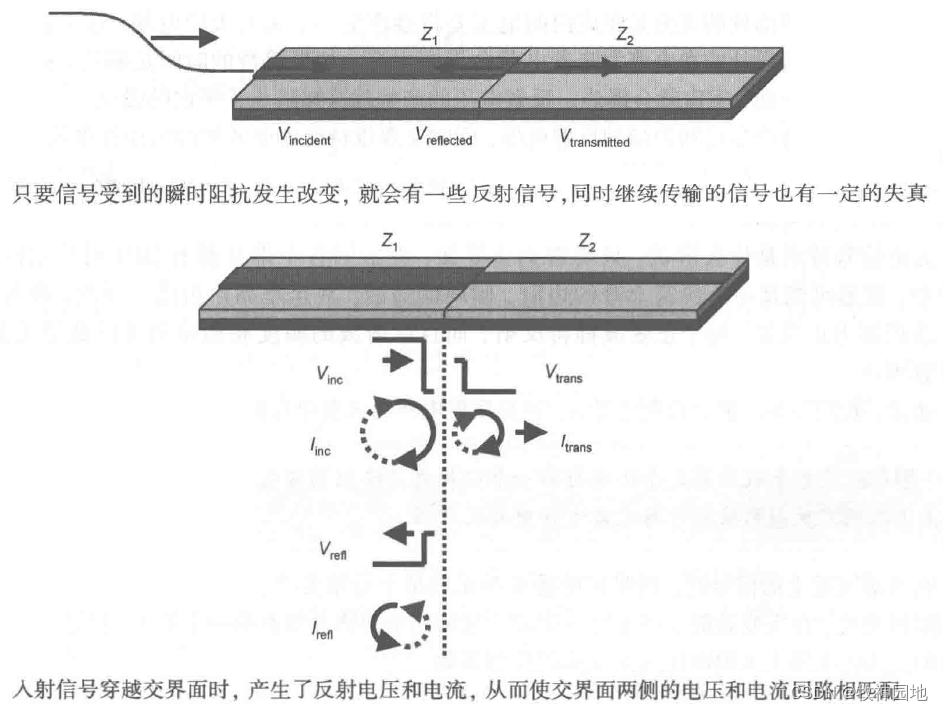
如上图所示，那我们用V入射，V反射，V传输来表示信号在阻抗交界面产生的电压，其对应的电流分别是I入射，I反射，I传输；电流和电压关系需满足：V入射+V反射=V传输；I入射-I反射=I传输；那么，V入射/Z1 - V反射/Z1 = V传输/Z2； à V入射/Z1 - V反射/Z1 = （V入射+V反射）/Z2；可得：       ρ = V反射/V入射=（Z2-Z1）/（Z2+Z1）；t = V传输/V入射= 2*Z2/（Z2+Z1）。

——ρ：反射系数；t：传输系数。

举个栗子：我们从下图传输线信号传输模型来定性理解阻抗突变导致的反射现象，假设Z0=50ohm，Z1=100ohm，输入电压V=5V；传输线电流在阻抗突变交接前电流是：5V/50ohm = 100mA；由于传输线上存在电感，电流不能突变，考虑极端情况：100mA全部电流涌入Z1（100ohm），那么此处会产生电压V2 = 100ohm*100mA = 10V，此时传输（Z1）电压大于入射（Z0）电压5V，那么必将产生一个反射电流I反= (5V-10V)/50ohm = -100mA。而在实际情况中，当电压上升到大于5V后，电感两端产生反向电压，正向流入的电流迅速减小，同时产生反射电流/电压，传输电流不会上升到100mA的极限值，最终形成一个平衡。

三，传输线信号反射过程

1，低源端阻抗无匹配传输线

如下图所示，假设驱动器内阻为10ohm，无损传输线阻抗为50ohm，终端阻抗∞（开路/无匹配）；信号传输的过程如下：

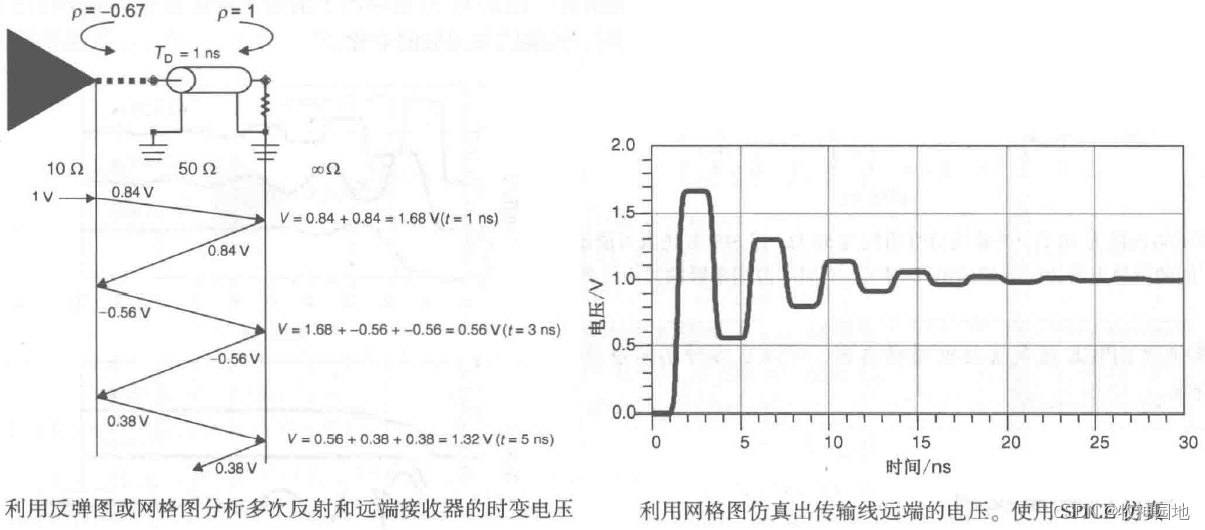
1. 信号从源端发出电压沿着传输线传输，从传输线模型可知此时驱动器内阻与传输线阻抗形成分压关系，V源端1 = [50/(10+50)]*1V = 0.84V；

2. 经过阻抗连续的无损传输线，Td = 1ns的延时，信号V源端1无损耗的传播到终端，信号幅度为0.84V；

3. 此时在终端开路，阻抗为∞，传输线阻抗不连续而发生发射，反射系数为：(∞-50)/(∞+50) = 1，表示全反射；终端电压幅度V终端1 = 0.84V+0.84V=1.68V，此时有0.84V电压从终端反射回源端；

4. 信号到达源端后，源端阻抗为10ohm，注意反射回源端时这个10ohm是并联在电源轨道上，此时电源等价于回流路径，所以不是分压而是反射；反射系数为：（10-50）/（10+50）= -0.667，反射电压 V源端反射1 = 0.84V*（-0.667）= -0.56V，  V源端2 = 0.84V–0.56V=0.28V；

5. V源端反射1 电压（-0.56V）经传输线再传输到终端，终端全反射，所以终端电压V终端2 =1.68V-（0.56V*2）= 0.56V；

6. 同理-0.56V（反射电压）再传输回源端，至此形成一个振荡，其振荡频率为传输线延时的4倍；振荡幅度不断衰减直至输出信号电压1V。

如上为低源端阻抗无损传输线模型的举例说明，我们用参数代入上述反射过程，完整的有损传输线反射函数如下图所示，其中：

1. A(ω)= Z0(ω)/[Zs(ω)+Z0(ω)]，源阻抗与传输线阻抗分压；

1, 有一个问题是：为什么是源端信号最初发出来的信号与特征阻抗是分压关系？

(1) 如下图所示，当一个高电平信号Vo刚刚从器件中发出，它首先是经过了一个串联的内阻Zs；

——如果外接了源端串联匹配电阻，那么Zs包括匹配电阻，要求是串联匹配电阻与芯片之间的距离满足集总模型长度（即，走线长度要小于1/10的信号波长），这也是为什么源端匹配尽量靠近发送端的原因。

(2) 信号传播到传输线上后，受到一个传输线的特征阻抗Z0，我们上一章已经说明了，Z0是信号路径相对于回流路径的阻抗（即如下图），并非如源端的阻抗（内阻和源端匹配）是串在信号路径上的；

(3) 现在就是一个非常简单的计算了，V1 = Vo*Z0/(Zs+Z0)。

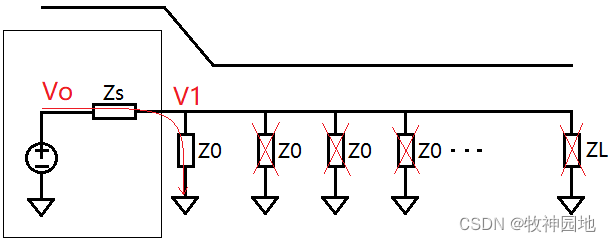
2, 第二个问题是：为什么信号在理想传输线的传输过程中不会产生反射呢？

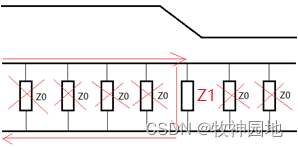
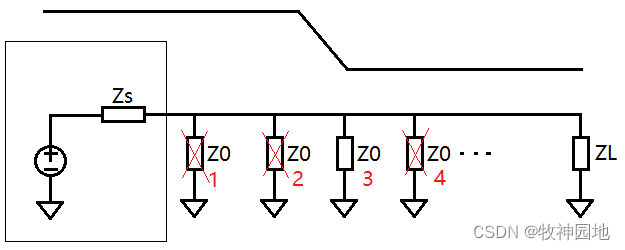
(1) 如下图所示，假设信号在传播过程中，从第2个Z0切换到了第3个Z0，此时传输线上的电流并不会发生变化，即电流一直处于连续状态，所以电压也不会发生变化；

——如下示意图中，特征阻抗是分离开的一个个Z0，这只是为了便于理解；实际传输线上的特征阻抗并非是离散的，而是随着信号边沿的传播过程而非常连续的：当信号边沿连续从左往右传播时，一部分传输线结束了充放电（L+C），另一部分则开启了充放电（L+C）。

2. Hx(ω) = exp √{-x[(R(ω) + jωL)*(jωC)]}，传输线传递函数，包含传输线损耗和延时；

——传输线传递函数涉及到了指数函数，我们后续再详细分析指数函数，这里只需要看一看传输线的传递函数长啥样就行。

3. T(ω)= [2*ZL(ω)]/[ZL(ω)+Z0(ω)]，终端传输系数

——传输系数，即传输过去的信号幅度比例。

4. R2(ω) = [ZL(ω)-Z0(ω)]/[ ZL(ω)-+Z0(ω)]，终端反射函数；终端反射是如何发生的呢？

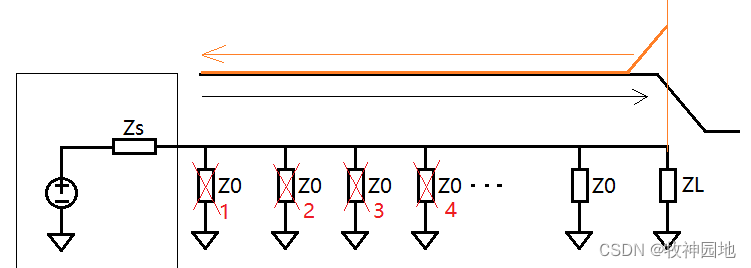
1, 如下图所示，当信号传输至终端时，原来传输线上的电流I0 = V0/Z0，但是ZL > Z0的话：IL = V0/ZL，此时IL < I0，必然会多出一部分电流没地方去，只能原路返回。

——举个栗子，假如ZL为无穷大，那么这些电流没地方流出去，只能全部返回回来，所以此时的电流I = 2*I0，那我们可以根据欧姆定律得到电压V = 2*I0*Z0 = 2*V0；这是全反射的情况。

5. R1(ω) = [Zs(ω)-Z0(ω)]/[ Zs(ω)-+Z0(ω)]，源端反射函数。

1, 上面说源端信号传递的模式是分压的，为什么又是反射了呢？

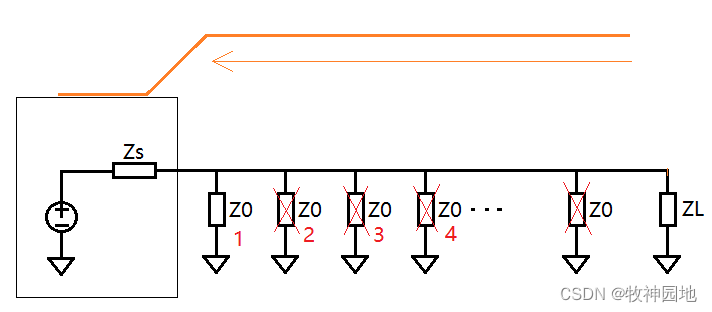
(1) 如下图所示，当从终端反射回来的信号边沿到达源端，源端阻抗Zs是一端连接至Vcc或GND的；

(2) 如果Zs是接到GND（即，输出驱动为低），那么就比较好理解，它在电路结构中的位置等价于特征阻抗Z0和终端阻抗ZL，所以其也是有传输系数和反射系数的；

(3) 如果Zs是连接到VCC（即，输出驱动为高），怎么理解呢？我们上一章跟大家明确过了，需要摒弃回流是GND的这种错误观念，在信号回流上VCC和GND是等价的，VCC就可以当做GND。

——VCC和GND之间对于高频信号来说，一般是低阻抗通道，举个栗子：VCC和GND之间的电容为10uF，那么在10MHz下的阻抗是：Zc = 1/(2*π*f*C) = 1/(2*3.14*107*10*10-6) = 1.6mΩ，可以相互等价。

这部分是信号反射和阻抗匹配的理论基础，一定要搞清楚整个传输过程，而不是流于表面。因为实际信号传输比这个理想模型复杂的多，基本原理没搞清楚的话，一旦涉及到具体问题，就容易出现玄学的幻觉。

2，短线

当输入信号的边沿时间足够长（线长<1/6 Tr），所有错开振荡部分会混合叠加，不会产生振铃现象，仅当信号上升时间能够与信号在传输线上的延迟差不多甚至更小时（长线），才会出现明显的过冲和振铃。

根据如上的理论推导，在短线模式下传输线的损耗和延时都可以忽略不计，且T(ω)= R2(ω)+1；可以将传输函数简化：Sshort(ω)= [A(ω)*(R2(ω)+1)]/[1-(R2(ω)*R1(ω)] ，将函数代入源端阻抗Zs，传输线阻抗Z0，终端阻抗ZL计算，Sshort(ω) = ZL/(ZL+Zs)。

得到一个重要的结论：在短线模式下的传输模型是由负载阻抗ZL和源端阻抗Zs构成的简单阻抗分配网络。

——源端串联阻抗匹配有用么？当然有用，串阻叠加到Zs上，从而减小接收端信号电压幅度。

3，高源端阻抗无匹配传输线

源端阻抗值大，主要体现在源端阻抗分压：A(ω) =Z0(ω)/[Zs(ω)+Z0(ω)] 和源端反射系数：R1(ω) = [Zs(ω)-Z0(ω)]/[ Zs(ω)+Z0(ω)]上，而传输到终端后反射系数：R2(ω) = [ZL(ω)-Z0(ω)]/[ ZL(ω)+Z0(ω)] = 1，是全反射（因为理想终端阻抗ZL(ω)是无穷大）。

1. 此时由于Zsω很大导致A(ω)很小，所以高源端阻抗时初始输出的阶跃非常小；

——举个栗子：假如源端阻抗Zs(ω)=1000Ω，特征阻抗Z0(ω) = 50Ω，那么源端分压A(ω) = 50/(1000-50) = 1/19，如果是3.3V电平信号，那么在经过第一次阻抗分压之后的电压是0.17V。

2. R1(ω)很大说明信号从终端反射回源端时也产生了较大幅度反射，在确定的时间段内，其最终值等于输入阶跃值；

——根据上面的栗子：R1(ω) = (1000-50)/(1000+50) = 950/1050 = 0.9，注意：反射系数为0.9表示很大的反射（全反射的系数为1），如果反射系数为0表示没有反射，反射系数为-1表示全吸收。

如下图所示，我们可以得到这种阶跃非常像RC滤波的响应（缓慢的上升，类似于RC充电），阶跃响应的建立时间段与源阻抗和线上负载电容的乘积相近；由于高源端阻抗无匹配传输线阶跃响应与RC滤波的相似性，可以把传输线的输入看做容性负载，所以在线路匹配设计时，如果串入电阻过大时，现象是：无过冲，但边沿会变缓。

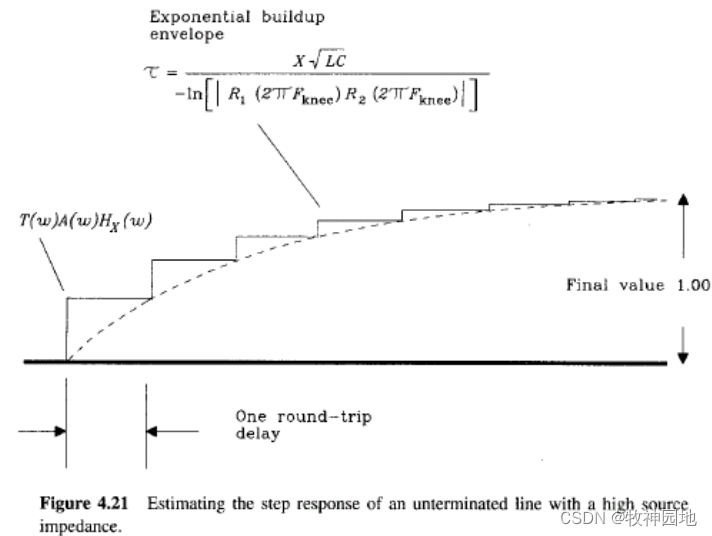
4，中间容性负载传输线

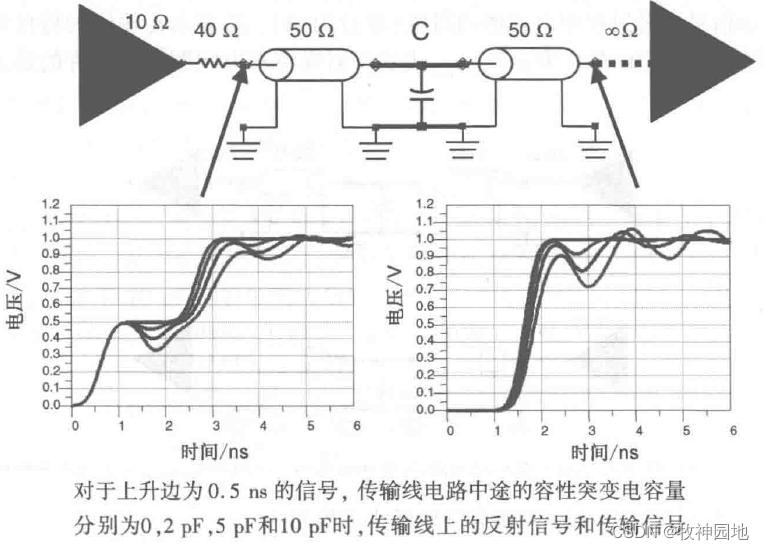
假设一种最简单的情况：一个电容器并接在传输线的中间位置（电容器的左右两侧传输线都是无线长），此时信号会在此处产生两部分信号：反射信号（反射系数）和传输信号（传输系数）。

1. 在并接电容器的位置，其阻抗Z = Zc | Z0（并联），可得容性反射系数Rc(ω) = -jω*C*Z0/(2+ω*C*Z0)；我们可以得到：如果反射系数为Rc(ω) = 1，当fmax = 1/(2*C*Z0*π)时，将发生全反射，所以不可以将传输线使用在该频率上；

——举个栗子，假设Z0=50ohm，C=1nF，那么 fmax ≈ 6.4MHz时几乎是全反射。

2. 如果信号频率在该频点以下，那么反射系数等于输入阶跃的导数：-C(Z0/2)。

——如果数字信号拐点频率小于fmax，对信号传输看起来使一个低通滤波器，减慢输入信号的上升时间，响应时间（10%~90%）：Tr = 2.2C*Z0/2。

5，等间隔容性负载传输线

有一种电路模型，与原来的模型相比有相同的电感和电阻，但有不同的电容值；举个栗子：1驱多的DDR/Nand Flash 拓扑结构，每片DDR/Nand Flash颗粒相当于增加了一个容性负载；我们将这个容性负载值加到现存传输线的单位长度电容上，得到新的传输线模型电容值。

如下图所示，此时得到一个重要的结论：等间距多容性负载新模型的传输线阻抗会变小，传输延时会增加，在阻抗匹配和时序设计时要另外考虑。

——我们从该栗子可以看到：传输线上信号传播速度和特征阻抗取决于在传输过程中受到感抗和容抗的组合： Z = LC，介电常数和磁导率只是这两个参数的另外一种方式的呈现，所以虽然介电常数和磁导率不变，如果还有其它外部条件改变了信号传播过程中的感抗和容抗，那么还是会影响到其传播速度和传输线阻抗。

6，直角转弯传输线

记得大学毕业设计，用Protel 99se画了一块CPLD逻辑控制的实验板，板子画的跟14英寸屏幕一样大，走线也是非常随意，没有一根不是直角；毕设导师看了后说：你这板子画太大了，而且走线最好不要走直角，来不及给你改了。为什么要求PCB走线不能走锐角或者直角呢？我当时觉得可能不大美观？

如下图所示，当走线是直角时：直角弯曲导线的有效宽度增大了，从而产生了不需要的额外寄生电容，就像是附在传输线上的一个容性负载。有了这个容性负载传输线的瞬时阻抗将会发生变化（产生阻抗不连续点），根据中间容性负载传输线章节所述，在此会产生一个反射，影响信号质量。

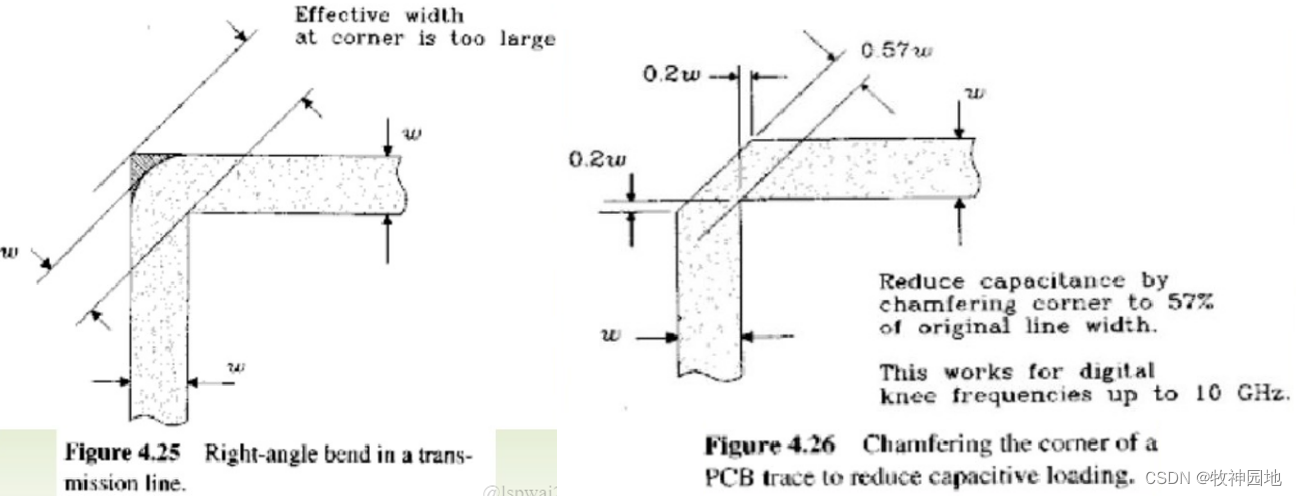
如上图所示，解决传输线直角的问题，有两种解决方案：

1. 将直角做成圆角，是的传输线的宽度保持固定，改善信号反射以及信号上升沿时间的不良影响；

2. 对直角进行斜切（45°），计算上升沿时间常数（如右下图），这个上升时间的值很小，可以满足上升沿大于100ps（差不多对应10GH以内的信号）的高速信号应用。