台大李宏毅机器学习—学习笔记07

熵： 熵（entropy）指的是体系的混乱的程度，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。
信息熵（香农熵）： 是一种信息的度量方式，表示信息的混乱程度，也就是说：信息越有序，信息熵越低。
信息增益： 在划分数据集前后信息发生的变化称为信息增益。

为了计算熵，我们需要求关于H(X)在以p(x)分布下的信息量的数学期望：

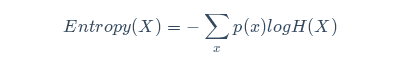
条件熵：条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵(conditional entropy)H(Y|X)，定义为X给定条件下Y的条件概率分布的熵对X的数学期望：

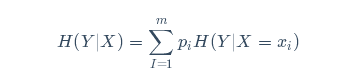
联合熵：对服从联合分布为P(x,y)的一对离散随机变量(X,Y)，其联合熵H(X,Y)可表示为：

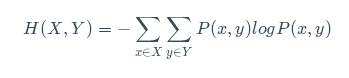
相对熵：又称交叉熵，KL散度等

        如果我们对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，我们可以使用 KL 散度（Kullback-Leibler (KL) divergence）来衡量这两个分布的差异。P(X),Q(X)的比值取对数之后，在P(X)的概率分布上求期望：

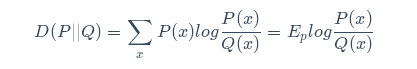
 交叉熵：

计算给定数据集的香农熵的函数:

def calcShannonEnt(dataSet): # 求list的长度，表示计算参与训练的数据量numEntries = len(dataSet) # 计算分类标签label出现的次数labelCounts = {} # the the number of unique elements and their occurance for featVec in dataSet: # 将当前实例的标签存储，即每一行数据的最后一个数据代表的是标签currentLabel = featVec[-1] # 为所有可能的分类创建字典，如果当前的键值不存在，则扩展字典并将当前键值加入字典。每个键值都记录了当前类别出现的次数。if currentLabel not in labelCounts.keys(): labelCounts[currentLabel] = 0 labelCounts[currentLabel] += 1 # 对于 label 标签的占比，求出 label 标签的香农熵shannonEnt = 0.0 for key in labelCounts: # 使用所有类标签的发生频率计算类别出现的概率。prob = float(labelCounts[key])/numEntries # 计算香农熵，以 2 为底求对数shannonEnt -= prob * log(prob, 2) return shannonEnt