多目标优化NSGA-II(快速精英非支配排序遗传算法)及python实现

前言

NSGA-II适用于复杂的多目标优化问题，是K-Deb教授在2000年在一篇paper《MOEAs — A fast and elitist multi-objective genetic algorithm: nsga2》提出。

Keywords： optimization; multi-objective evolutionary algorithm; non-dominated sorting genetic algorithm II (NSGA-II); genetic algorithm(GA)；crowding-distance

原文链接: http://repository.ias.ac.in/83498/1/2-a.pdf.

一、什么是NSGA-II？

在过去的十年里，许多多目标进化算法被提出。主要原因是他们能够在一次运行中找到多个帕累托最优解。由于问题具有多目标公式的主要原因是不可能有一个同时优化所有目标的单一解，因此给出大量位于帕累托最优前沿或其附近的备选解的算法具有很大的实用价值。

The Non-dominated Sorting Genetic Algorithm (NSGA) 是此多目标进化算法之一。

但是NSGA有一些问题：

• 非支配排序高的计算复杂度: 复杂度为$O\left(m{N}^3\right)$
• 缺乏elitism: 精英主义可以显著加快遗传算法的性能。
• 需要制定共享参数: 严重依赖于共享的概念。

NSGA-II的出现解决了这些问题。

二、学习NSGA-II

1.快速非支配排序算法

为了根据非支配水平大小为N的种群进行排序，必须将每个解与种群中的每个其他的解进行比较，以发现它是否被支配。

什么是支配？

​ 比如一个女生和另外一个女生比较身高和体重，如果1号女生既比2号女生高又比2号女生瘦，此时1号女生支配2号女生。如果1号女生只比2号女生高，但是比2号女生瘦，这说明两个女生身材不分伯仲，此时谁都不支配谁。

首先，我们对于每个解，计算两个实体：

• $n_i$支配解的数量。

• $S_i$支配解$i$的一组解

  这两个实体的计算复杂度为$O\left(m{N}^2\right)$。

  我们要找到所有$n_i=0$的点，并把它放入一个$F_1$列表中。现在，对于$F_1$证监会中每一个解决方案，我们访问其$S_i$集合中的每一个成员j，并将n计数减少1。如果对于任何一个成员j的计数变为0，就将它放入单独的列表h中。当$F_1$中所有成员被检查过，将$F_1$作为一级非支配层。然后，继续循环，使用h作为下一次循环的$F_1$。以此类推，直到整个种群被分层。

2.密度估计

为了估计人口中特定点周围解的密度，我们沿着每个目标取该点两侧两点的平均距离。这个数值作为以最近邻居作为顶点的长方体周长的估计。

3.拥挤比较算子

经过快速非支配排序以及计算拥挤度之后，种群中每个人口有两个属性：

• 非支配等级

• 局部拥挤距离

  也就是说，在具有不同非支配等级的两个解之间，我们具有较低等级的点更好。如果两个点都属于一个等级，那么位于点数较少的区域的点（包含它的长方体的大小较大）更好。

4.主循环

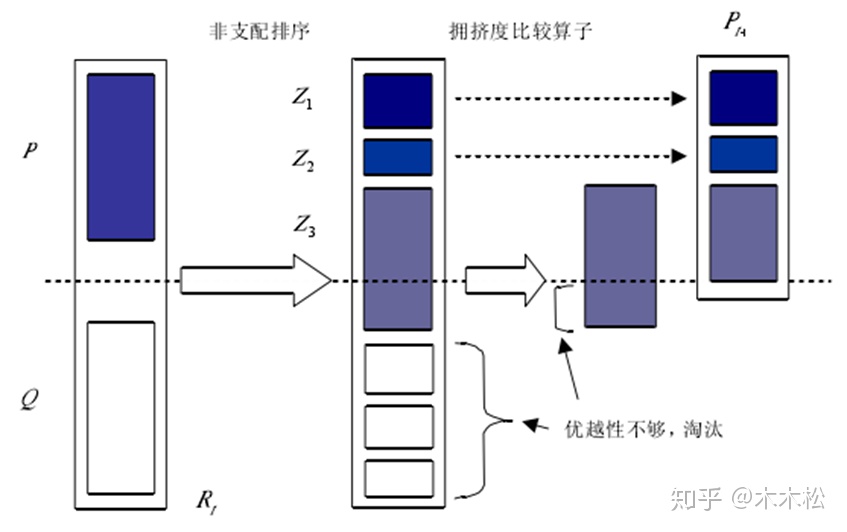
最初，创建随机的父群体$P_0$，对种群进行非支配排序。每个解被分配一个与其非支配等级级别相等的适应度。Binary tournament、重组、变异操作符用于创建大小为n的子种群$Q_0$。精英策略伪代码如下所示：

首先，将t代产生的新种群$Q_t$与父代种群$P_t$合并。群体大小为2N。然后，进行非支配排序。新的父群体$P_{t+1}$是累加的，直到填满N。这个n个大小的种群现在用于选择、交叉和变异，以创建新种群$Q_{t+1}$。

精英策略：

5.代码

使用geatpy遗传算法工具库可以实现NSGA-II算法。后期会介绍，敬请期待！

6.总结