本文主要是介绍论文解读:Adaptive Particle Swarm Optimization (APSO),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
模糊集、隶属度函数的概念,以及如何确定隶属度函数
- 动机
- 主要贡献
- 演化状态估计(evolutionary state estimation, ESE)
- PSO中的中群分布信息
- 演化状态估计(ESE)
- 模糊状态分类(Fuzzy)
- 参数自适应控制策略
- 精英学习策略(elitist learning strategy, ELS)
- 自适应PSO算法(APSO)框架
这里,通过分享一篇2009年发表在TCYB上的论文举例说明模糊数学在智能优化算法中的实际应用。
动机
- PSO与其他基于种群的迭代算法相似,根据所需的函数评估次数来衡量,该算法在计算上可能效率低下。当解决多模态问题时,该算法容易陷入局部最优的困境。这些缺陷已经限制了PSO的广泛应用。
- 加快收敛速度同时避免局部最优值称为PSO搜索过程中的两个重要且吸引人的目标。为了达到这两个目标,有相当数量的PSO变体已经被研究。遗憾的是,在这篇文章之前,很难有文章能够同时满足这两个目标。
- PSO 中的惯性权重 ω \omega ω 用于平衡全局和局部搜索能力。 很多研究者主张 ω \omega ω 的值在探索状态应该大,在探测状态时应该小,但是单纯随时间减小 ω \omega ω 不一定正确。
- 加速系数 C 1 C_1 C1表示“自我认知(self-cognition)”通过将粒子拉到自身历史最佳位置来维持群体多样性;加速系数 C 2 C_2 C2为“社会影响(social influence)”,通过推动群体向当前全局最佳区域收敛来实现算法的快速收敛。这是两种不同的学习机制,应该在不同的进化状态下给予不同的处理。
- 当搜索进入收敛阶段时,如何让算法跳出局部最优值是找到全局最优解的关键。
主要贡献
- 开发了一种参数自适应方法和精英学习策略,使得算法能够在加速收敛和全局搜索两个方面提升PSO算法的性能。其中,精英选择策略将维持种群的多样性以便使算法能够跳出潜在的局部最优值;
- 为了能够实现自适应,设计了一种基于模糊的演化状态评估技术。因此,PSO参数不仅受到ESE的控制,而且还考虑了这些参数在不同状态下的不同影响;
演化状态估计(evolutionary state estimation, ESE)
在一个PSO过程中,种群的分布特征不仅随着代数变化而且随着演化状态的变化而变化。例如,早期阶段,粒子可能分散在不同的地方,此时,种群的分布是分散的。但是,随着演化过程的进行,粒子可能会聚集在一起并收敛在局部或全局最优值区域。因此,种群的分布信息在搜索的早期和后期是不同的。因此,我们首先讨论如何识别不同的种群分布信息以及如何利用这些信息估计演化状态。
“演化状态”概念最早由zhang和zhan在2007年提出。不同的是,这里通过模糊分类选择扩展了惯用的ESE方法。
PSO中的中群分布信息
为了用公式描述ESE,首先应该研究种群的分布特性。这里以一个时变2-D球形函数
f 1 ( x − r ) = ( x 1 − r ) 2 + ( x 2 − r ) 2 f_1(x-r) = (x_1-r)^2 +(x_2-r)^2 f1(x−r)=(x1−r)2+(x2−r)2为例说明粒子在PSO过程中的分布动态,其中 r r r初始化为-5并在一个100代的优化过程中的第50代的时候转换为5。也就是说, f 1 f_1 f1的理论最小值在搜索的中间阶段时从(-5,-5)转为(5,5)。Fig.1显示了不同运行阶段的种群分布情况

从Fig.1(a)可以看出,初始化之后,粒子在没有一个明显的控制中心的情况下开始探索整个搜索空间。然后,如Fig.1(b)所示,PSO的学习机制使得许多粒子向最有区域聚集。然后,如Fig.1©所示,种群向最佳粒子收敛。在第50代的时候,球的底部从(-5,-5)变为(5,5),由此可见,Fig.1(d)中出现了一个远离当前集群的新leader。如Fig.1(e)所示,它引导种群从之前的最有区域跳出至新的区域,并形成一个如Fig.1(f)所示的二次收敛。
基于以上观察可知,种群的分布信息可以在运行时发生显著地变化。
进一步地,通过计算每个粒子到其他粒子的平均距离,可以将Fig.1描述为Fig.2。
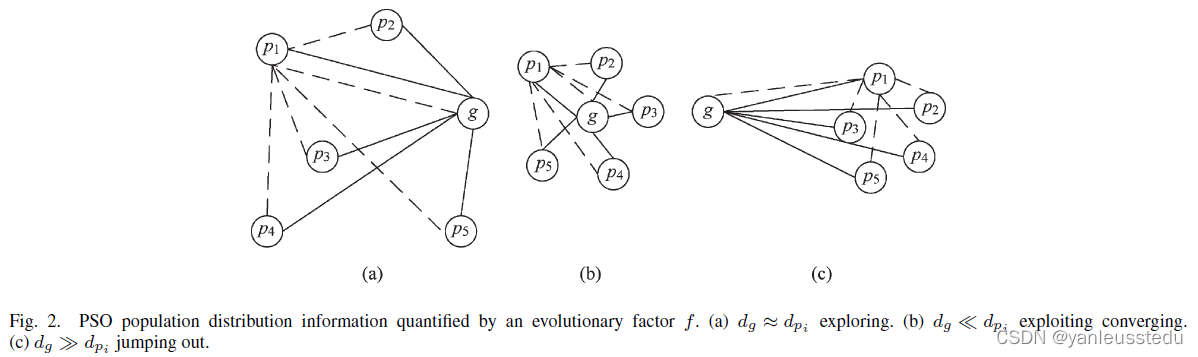
ESE方法将在每一代中考虑种群的分布信息,具体步骤如下:
Step1: 计算每个粒子 i i i到其他粒子的平均欧式距离
d i = 1 N − 1 ∑ j = 1 , j ≠ i N ∑ k = 1 D ( x i k − x j k ) 2 d_i = \frac{1}{N-1}\sum^N_{j=1,j\neq i}\sqrt{\sum^D_{k=1}(x^k_i - x^k_j)^2} di=N−11j=1,j=i∑Nk=1∑D(xik−xjk)2
其中, N N N和 D D D分别是种群规模和维数。
Step2: 计算“进化因子 f f f”
f = d g − d m i n d m a x − d m i n ∈ [ 0 , 1 ] f = \frac{d_g - d_{min}}{d_{max} - d_{min}}\in [0,1] f=dmax−dmindg−dmin∈[0,1]
其中, d g d_g dg是全局最佳粒子到其他粒子的平均距离, d m a x d_{max} dmax以及 d m i n d_{min} dmin分别所有粒子平均距离的最大值以及最小值。
演化状态估计(ESE)
Fig.3记录了几个函数的 f f f值动态,从图中可以看出,通过 f f f可以鲁棒地揭示PSO在运行时的动态。即,探索阶段大约出现在前6代,此时 f f f较大,然后 f f f快速下降,算法进入探测阶段,一直到大约第25代。之后为收敛阶段,此时 f f f会消失,直到环境发生变化。当搜索目标在第50代发生变化时,PSO似乎可以跳出当前最优值,并导致一个最大的 f f f值。随之而来的是再一次的探索和探测,直到出现下一次收敛。

根据 f f f值的不同,可以分为四种状态, S 1 S_1 S1, S 2 S_2 S2, S 3 S_3 S3和 S 4 S_4 S4,分别代表 e x p l o r a t i o n exploration exploration, e x p l o i t a t i o n exploitation exploitation, c o n v e r g e n c e convergence convergence和 j u m p i n g o u t jumping out jumpingout。这些集合可以进行简单地均匀分配,或称为严格分类(rigid classification),如:

模糊状态分类(Fuzzy)
然而,基于对Fig.1-3的分析可知,状态转换可能是不确定的和模糊的,并且不同的算法和应用表现出不同的转换特征。因此,这里采用模糊分类方法。
众所周知,隶属函数是模糊分类的关键。对于不同阶段隶属函数描述如下:




进一步地,可以画出集合 S 1 S_1 S1, S 2 S_2 S2, S 3 S_3 S3和 S 4 S_4 S4对应的梯形型隶属函数关系图:

关于模糊数学的相关知识,请参阅中南自动化学院“智能控制与优化决策“至渝提供的博文,感谢博主!!
同时,这里采用singleton方法进行去模糊。
参数自适应控制策略
- Adaption of the Inertia Weight
这里利用Sigmoid映射使得 w w w可以随着演化状态而变化:
w ( f ) = 1 1 + 1.5 e − 2.6 f ∈ [ 0.4 , 0.9 ] w(f) = \frac{1}{1+1.5e^{-2.6f}}\in[0.4,0.9] w(f)=1+1.5e−2.6f1∈[0.4,0.9]
可以看出, w w w的变化受演化因子 f f f的控制而与时间 t t t无关,因此 w w w是关于 f f f的单调增函数。换句话说,在 S 1 S_1 S1和 S 4 S_4 S4种,较大的 f f f将导致一个较大的 w w w值,这有利于进行全局搜索。相反,当 f f f较小时,算法进入探测或者收敛阶段,此时算法将获得一个较小的 w w w值,这有利于进行局部搜索。 - Control of the acceleration Coefficients
在PSO算法种,加速因子有两个,其中, c 1 c_1 c1表示“self-cognition”,负责将粒子推向其自身的历史最优位置,这有助于探索局部小生境并维护群体的多样性。 c 2 c_2 c2表示“social influence”,负责推动群体向当前全局最优区域收敛,从而加快收敛速度。
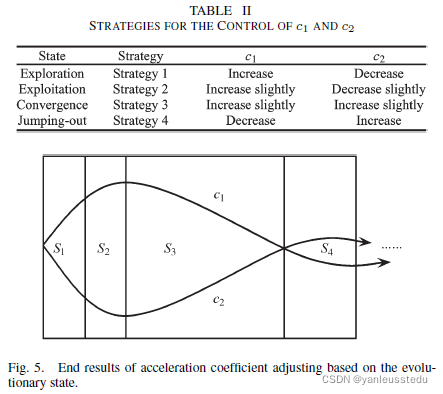
下面给出每个阶段对 c 1 c_1 c1和 c 2 c_2 c2的控制策略(TABLE ||)及其变化曲线(Fig. 5):
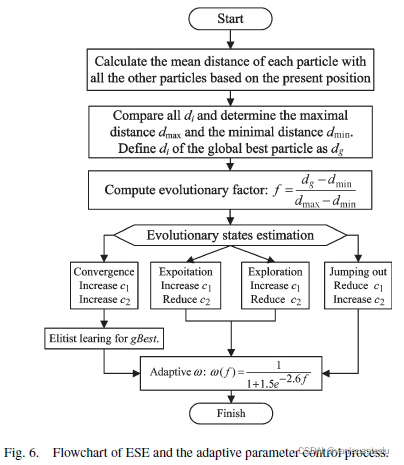
完整的基于ESE的自适应参数控制过程如下:
精英学习策略(elitist learning strategy, ELS)
Jumping-out机制对于提高算法的全局性是必要的。
具体做法是,

其中, P d P^d Pd表示第 d d d个维度, G a u s s i a n ( μ , σ 2 ) Gaussian(\mu, \sigma^2) Gaussian(μ,σ2)为均值为0,标准差为 σ \sigma σ的高斯分布随机数。

自适应PSO算法(APSO)框架

这篇关于论文解读:Adaptive Particle Swarm Optimization (APSO)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






