数据结构（三）：栈及面试常考的算法

本文主要是介绍数据结构（三）：栈及面试常考的算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、栈介绍

1、定义

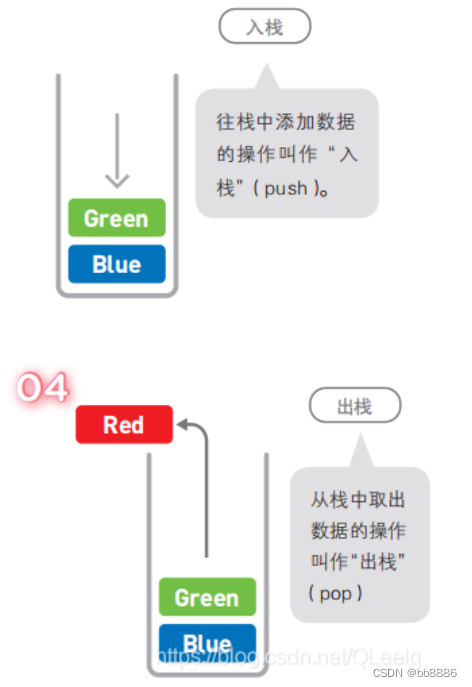
栈也是一种数据呈线性排列的数据结构，不过在这种结构中，我们只能访问最新添加的数据。从栈顶放入元素的操作叫入栈，取出元素叫出栈。

2、优缺点及使用场景

优点：高效的操作、简单易用、空间效率高等

缺点：局限性、容量限制、内存管理、不支持随机访问等。

使用场景：递归算法、括号匹配、表达式求值等。

3、基本操作

Push--在顶部插入一个元素

Pop--返回并移除栈顶元素

isEmpty--如果栈为空，则返回true

Top--返回顶部元素，但并不移除它

二、常考算法

1、使用栈计算后缀表达式

题目：根据逆波兰表示法，求表达式的值。

示例：输入: ["10", "6", "9", "3", "+", "-11", " * ", "/", " * ", "17", "+", "5", "+"]，输出: 22

逆波兰表达式主要有以下两个优点：

去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
适合用栈操作运算：遇到数字则入栈；遇到运算符则取出栈顶两个数字进行计算，并将结果压入栈中。

#include<stack>
#include<vector>
#include<string>
#include<iostream>
using namespace std;int evaluate_postfix(vector<string> v){stack<long long> st;for(int i = 0; i < v.size(); i++){if (v[i] == "+" || v[i] == "-" || v[i] == "*" || v[i] == "/"){long long num1 = st.top();st.pop();long long num2 = st.top();st.pop();if(v[i] == "+") st.push(num2 + num1);if(v[i] == "-") st.push(num2 - num1);if(v[i] == "*") st.push(num2 * num1);if(v[i] == "/") st.push(num2 / num1);}else{st.push(stoll(v[i]));}}int result = st.top();st.pop();return result;
}int main(){vector<string> v = {"10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"};int res;res = evaluate_postfix(v);cout << res;
}

2、对栈的元素进行排序

题目：input：[3, 1, 4, 2, 5] output：[5, 4, 3, 2, 1]

思路：从原始栈中取出元素，将其插入到结果栈中的正确位置，以实现排序。在Python中，使用了while循环和pop操作，而在C++中使用了while循环和top、pop操作。最终，返回的结果栈中包含了排序好的元素。

#include<stack>
#include<iostream>
using namespace std;
stack<int> sort_stack(stack<int> input_stack){stack<int> result_stack;while(!input_stack.empty()){int temp = input_stack.top();input_stack.pop();while(!result_stack.empty() && result_stack.top() < temp){input_stack.push(result_stack.top());result_stack.pop();}result_stack.push(temp);}return result_stack;}int main() {stack<int> input_stack;input_stack.push(3);input_stack.push(1);input_stack.push(4);input_stack.push(2);input_stack.push(5);stack<int> sorted_stack = sort_stack(input_stack);while (!sorted_stack.empty()) {cout << sorted_stack.top() << " ";sorted_stack.pop();}return 0;
}

3、判断表达式是否括号平衡

题目：给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。

示例：input："([{}]()"，output：False;

思路：主要分为以下三种情况：

（1）已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false。

（2）遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false。

（3）遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false。

技巧：在匹配左括号的时候，右括号先入栈，就只需要比较当前元素和栈顶相不相等就可以了。

#include<stack>
#include<string>
#include<iostream>
using namespace std;bool isvalid(string s){if (s.size() % 2 == 1) // 如果s的长度为奇数，一定不符合要求return false;stack<char> st;for(int i = 0; i < s.size(); i++){if (s[i] == '(') st.push(')');else if (s[i] == '{') st.push('}');else if (s[i] == '[') st.push(']');else if (st.empty() || st.top() != s[i])// 第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号 return false// 第二种情况：遍历字符串匹配的过程中，发现栈里没有我们要匹配的字符。所以return falsereturn false;       else st.pop(); // st.top() 与 s[i]相等，栈弹出元素}// 第一种情况：此时我们已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false，否则就return truereturn st.empty();}// 当bool类型的值为0时，它表示false，而当bool类型的值非零时，它表示true
int main(){bool s,s1,s2,s3;s = isvalid("([{}]()");cout << s << endl;s1 = isvalid("([{}}}");cout << s1<< endl;s2 = isvalid("([{}])))");cout << s2<< endl;s3 = isvalid("{[]}");cout << s3; 
}