本文主要是介绍0-1背包问题【穷举法+二维dp数组】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
问题描述:
使用穷举法解决0/1背包问题。问题描述:给定n个重量为{w1, w2, … ,wn}、价值为{v1, v2, … ,vn}
的物品和一个容量为C的背包,求这些物品中的一个最有价值的子集,且要能够装到背包中。
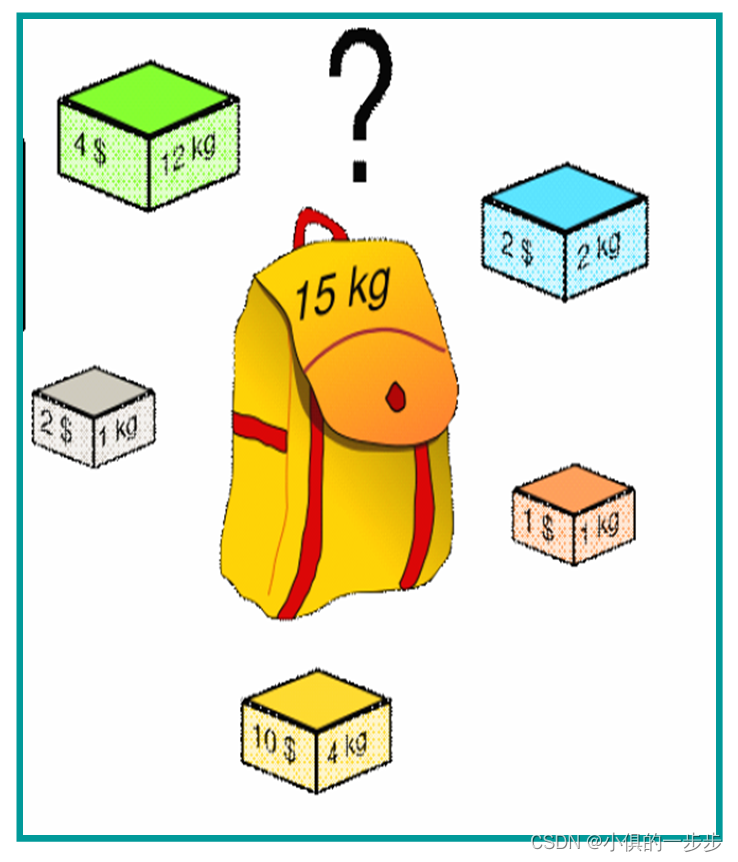
穷举法:每件物品装还是不装有两种选择,使用0-表示不装,1表示装,n件物品就有2^n种,穷举2^n种,找到符合符合weight背包容量的且为价值最大的方式。
public class Main01 {//穷举法public void pack01(int weight,int[] wt,int[] val){int n = wt.length;int count= (int) Math.pow(2,n);int maxVal = 0;//枚举32种情况,并且记录符合weight重量背包的最大价值for (int i = 0; i < count; i++) {String res = String.format("%5s",Integer.toBinaryString(i)).replace(' ','0');System.out.print(res+" ");int sumVal = 0;int sumWeight=0;for (int j = 0; j < n; j++) {//为1时表示装该物品 0表示不准装if (res.charAt(j)=='1') {sumVal += val[j];sumWeight += wt[j];}if (sumWeight<=weight){maxVal = Math.max(sumVal,maxVal);}}System.out.println("价值:"+sumVal+"重量:"+sumWeight);}//打印最大价值下对应的背包实际重量和所装物品的状态for (int i = 0; i<count; i++) {String res = String.format("%5s",Integer.toBinaryString(i)).replace(' ','0');int sumVal = 0;int sumWeight=0;for (int j = 0; j < n; j++) {if (res.charAt(j)=='1') {sumVal += val[j];sumWeight += wt[j];}}if (sumVal==maxVal&&sumWeight<=weight){System.out.println("当背包重量为"+weight+"时:最大价值:"+sumVal+" 总重量: "+sumWeight+" 方式:"+res);break;}}}public static void main(String[] args) {Main01 main01 = new Main01();int[] wt = {1, 2, 1, 12, 4};int[] val = {1, 2, 2, 4, 10};main01.pack01(15, wt, val);}
}输出结果:
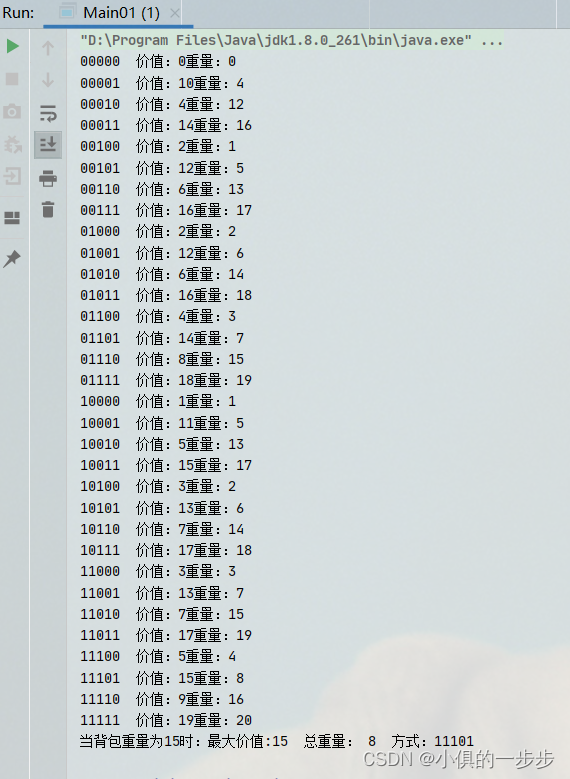
二维dp数组:
dp[i][w]数组含义:对于前i个物品,当前背包容量为w时,可装下的最大值是dp[i][w]。
dp[i-1][w-wt[i-1]]+val[i-1]:装物品i的价值
dp[i-1][w]:不装物品i的价值
因此dp[i][w]取装物品 i dp[i-1][w-wt[i-1]]+val[i-1] 和 不装物品i dp[i-1][w] 的最大值
public class Main01 {public static void main(String[] args) {int[] wt = {1, 2, 1, 12, 4};int[] val = {1, 2, 2, 4, 10};int res = pack01(15,wt,val);System.out.println("最大价值:"+res);}public static int pack01(int weight,int[] wt,int[] val){int n = wt.length;//dp[i][w]数组含义:对于前i个物品,当前背包容量为w时,可装下的最大值是dp[i][w]int[][] dp = new int[n+1][weight+1];for (int i = 1; i <= n; i++) {for (int w = 1; w <= weight; w++) {if (wt[i-1]>w){//不能装入背包dp[i][w] = dp[i-1][w];}else {//择优装入背包dp[i][w] = Math.max(dp[i-1][w-wt[i-1]]+val[i-1],dp[i-1][w]);}}}//打印dp表for (int i = 0; i <=n ; i++) {for (int j = 0; j <=weight ; j++) {if (j<weight){System.out.print(dp[i][j]+",");}else {System.out.print(dp[i][j]);}}System.out.println();}return dp[n][weight];}
}
输出结果:
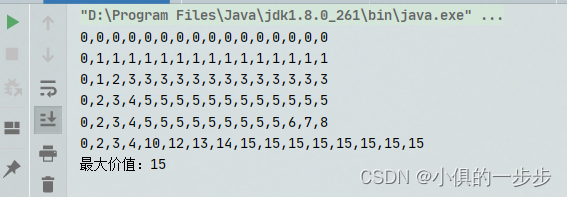
这篇关于0-1背包问题【穷举法+二维dp数组】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







