本文主要是介绍5.Vectors Transformation Rules,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在上节,有个问题:向量分量的转换方式 与 新旧基底的转换方式相反
用例子来感受一下,
空间中一向量V,即该空间的一个基底:e1、e2

v = e1 + e2
现把基底 e1 、 e2 放大两倍。变成

基向量放大了两倍, 但对于向量v ,其向量组件缩小了两倍。
它们两个 做了相反的事, 基向量放大, 某向量的向量组件缩小。 但V是不变的。
当使用新的基向量测量V时,V看起来更小,因为基向量变大了两倍
另一个例子:
旧基底:e1 、 e2 ; 新基底:。
向量V
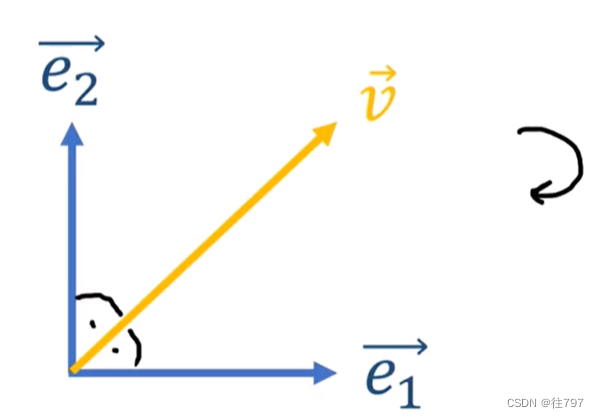
V 由大约相等的部分 e1 、e2组成, 且V与e1、e2的夹角大致相等。 意味着每个方向上的组件大致相同;

现顺时针选择这对基底, 使得V与的夹角 大于 V与
的夹角。 V不变
但V现在与相比,V更接近
, 这时,组件做了相反的事,V = x
+y
x肯定是 < y 的
回到上节最后那部分的内容,

当向量分量的行为方式 与 基向量的行为 相反 时,当基变大时,这是 完全有意义的。
意义:当基变大时,分量会缩小; 当基底向一个方向旋转时,组件 会向另一个方向旋转。
无论基底做什么,组件都会做 相反 的事。
通过这两个例子, 就能对2D中会发生这种相反的行为有了一定直觉。
那是否是在任何维度都如此呢?
证明 :(当然也是针对向量,旧基、新基的行为,组件的行为)
利用这个,以及之前的前向变换和后向变换。
代入,化简




以上就证明了,为从 旧组件 转移到 新组件, 我们实际上是 使用了 后向转换(Backward)
类似的,从新组件 转移到旧组件, 使用 向前转换(Forward)


现在因为向量分量的行为 与 基向量相反,
我们说 向量分量 是 Contra-variant
(向量是 逆变张量 vectors are contravariant tensors)
规定:
上述形式,改为:

这里向量V 已经被我们用 新基的线性组合或者旧基的线性组合写出,
但这些向量组件,因为它们是 CONTRA-variant。
我们将在编写方式上做点 改变,
把组件()的索引i写到字母v右上方,即
通过写在右上角,提醒 我们 组件是逆变的。
注意哦,把系数的i放到右上角, 其仍然是索引值,表示第 i 个,而不是 指数
基向量的索引是在右下角, 向量组件的索引在右上角,在某种程度上提醒了它们的行为方式相反
这篇关于5.Vectors Transformation Rules的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







