水声多径信道下LMS仿真(Python代码)

2023-10-30 19:10
文章标签 python 代码 仿真 水声 信道 多径 lms

本文主要是介绍水声多径信道下LMS仿真(Python代码)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 模块的导入

做仿真，numpy应该都知道
arlpy是水声通信工具箱，不仅可以产生信道的冲激响应，还有一些通信相关的函数
bokeh是用来画图的，配合jupyter notebook使用很爽！！（Matplotlib是常用的绘图工具包，个人感觉bokeh更舒服…）

# 数组运算工具包
import numpy as np
# 水声通信工具包
import arlpy.uwa as au
import arlpy.uwapm as aup
import arlpy.comms as ac
# 绘图工具包
from bokeh.plotting import show, figure
from bokeh.layouts import gridplot
from bokeh.io import output_notebook
output_notebook()
import warnings
warnings.filterwarnings('ignore')

2. 准备工作

2.1 水声信道的冲激响应

如何设置参数，得到冲激响应、衰减、时延等等在arlpy的官方文档中，都有介绍，可自行查阅
https://arlpy.readthedocs.io/en/latest/

# 设置环境参数
env = aup.create_env2d()
env['bottom_soundspeed'] = 1800
env['bottom_absorption'] = 0
env['depth'] = 100
env['max_angle'] = 30
env['min_angle'] = -30
env['frequency'] = 100
env['nbeams'] = 10
env['tx_depth'] = 20
env['rx_depth'] = 20
env['rx_range'] = 1000
# 假设声速在浅海环境下是递增的
sound_speed = np.zeros(shape=[6, 2])
for i in range(6):sound_speed[i, 0] = 20 * isound_speed[i, 1] = au.soundspeed(depth=20 * i)
env['soundspeed'] = sound_speedarrivals_sd = aup.compute_arrivals(env) # 声线到达的时间
delay_sd = min(arrivals_sd.time_of_arrival) # 端到端的传输时延
multidelay_sd = max(arrivals_sd.time_of_arrival) - \min(arrivals_sd.time_of_arrival) # 多径时延
fs = 100  # 信道的采样频率
cir_sd = aup.arrivals_to_impulse_response(arrivals_sd, fs=fs)
cir_sd = np.real(cir_sd)
cir_sd[(cir_sd < 0)] *= -1 # 信道的冲激响应

2.2 归一化及均衡代码

考虑到信道衰减比较大，在对信号进行处理的时候，需要考虑归一化的问题

def nor(x):'''param x: 带归一化信号return: 已归一化信号'''alpha = np.sum(np.square(x))/x.sizereturn x/np.sqrt(alpha)def equlization(sig_input, sig_expect, mu, M):'''param sig_input: 输入待均衡信号param sig_expect: 期望信号param mu: 均衡器步长param M: 均衡器长度return: (均衡后信号, 均方误差)'''n = sig_expect.sizeW = np.zeros(M)error = np.zeros(n)sig_output = np.zeros(n)if sig_input.size < n + M:sig_input = np.pad(sig_input, (0, n+M-sig_input.size))for i in range(n):input1 = sig_input[i:i+M]output = np.dot(W.T, input1)sig_output[i] = outputerror[i] = sig_expect[i] - outputW = W + mu * error[i] * input1J = np.square(error)return sig_output, J

3. 仿真

仿真的具体参数在调试时，有稍微改动，可自行调试

3.1 发射端

发射端使用了根升余弦滤波器进行滤波

N = 10000  # 数据点数
span = 4  # 升余弦滤波器范围
sps = 6  # 每符号采样率
rrc = ac.rcosfir(beta=0.5, sps=sps, span=span)
delay_rrc = int((rrc.size-1)/2)  # 经过滤波器之后，需要考虑滤波器的延迟sig_ori = ac.random_data(size=N, m=2) * 2 - 1
sig_exp = ac.upconvert(x=sig_ori, sps=sps, fs=0, fc=0)
sig_exp = nor(np.real(sig_exp))  # 使用ac.upconvert产生虚部为0的部分，为方便发图，取其实部
sig_tra = np.convolve(sig_exp, rrc)  # 发射滤波器的输出信号TOOLS = 'pan,box_zoom,xwheel_zoom,ywheel_zoom,crosshair,save,reset'  # 使用bokeh绘图时使用的交互工具
p1 = figure(tools=TOOLS, plot_width=800, plot_height=500,toolbar_location='above', toolbar_sticky=False)
p1.line(np.linspace(0, sig_exp.size-1, sig_exp.size),np.real(sig_exp), legend='sig_exp', line_color='red')
p1.line(np.linspace(0, sig_tra.size-1, sig_tra.size),np.real(sig_tra), legend='sig_tra-未考虑滤波器延迟',line_color='blue', line_dash='dashed')
p1.line(np.linspace(0, sig_tra.size-1-delay_rrc, sig_tra.size-delay_rrc),np.real(sig_tra[delay_rrc:]), legend='sig_tra-考虑滤波器延迟',line_color='green')
show(p1)

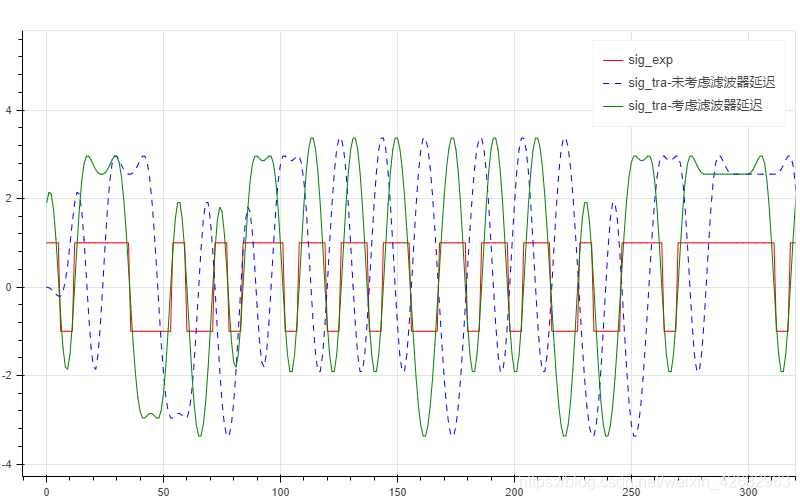
这个图是可以动的！

这个图是可以动的，横着拉，竖着拉，局部放大…（下面的图也是…）

3.2 多径信道

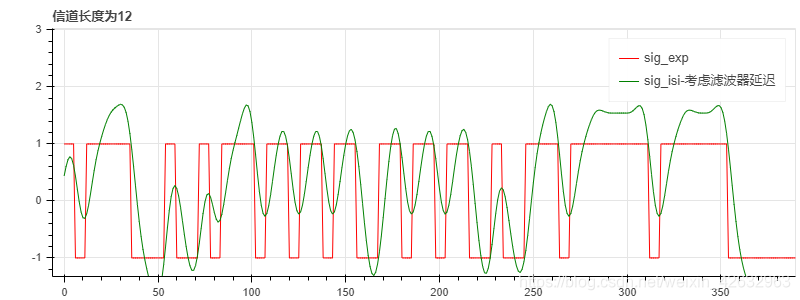
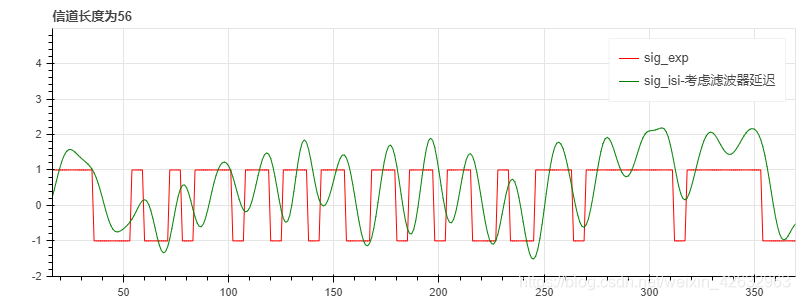
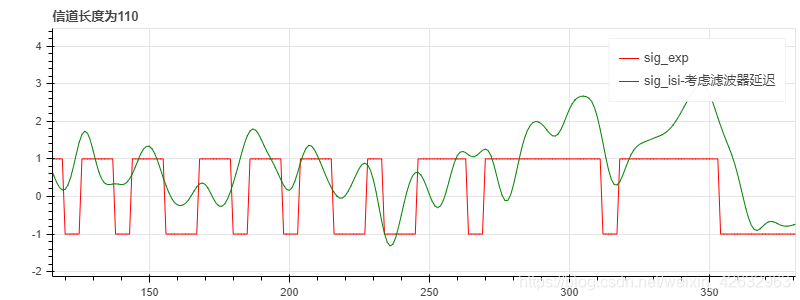
这里设置了三个不同的采样频率分别为100Hz，500Hz，1000Hz，得到的信道抽头个数分别为12,56,110，由仿真图可观察到采样频率越大，失真越严重

# fs = 100，信道长度为12
sig_isi1 = np.convolve(cir_sd, sig_tra)
sig_isi1 = nor(sig_isi1)p2 = figure(tools=TOOLS, plot_width=800, plot_height=300, title='信道长度为12',toolbar_location='left', toolbar_sticky=False)
p2.line(np.linspace(0, sig_exp.size-1, sig_exp.size),np.real(sig_exp), legend='sig_exp', line_color='red')
p2.line(np.linspace(0, sig_isi1.size-1-delay_rrc, sig_isi1.size-delay_rrc),np.real(sig_isi1[delay_rrc:]), legend='sig_isi-考虑滤波器延迟',line_color='green')fs = 500  # 信道的采样频率
cir_sd2 = aup.arrivals_to_impulse_response(arrivals_sd, fs=fs)
cir_sd2 = np.real(cir_sd2)
cir_sd2[(cir_sd2 < 0)] *= -1  # 信道的冲激响应
sig_isi2 = np.convolve(cir_sd2, sig_tra)
sig_isi2 = nor(sig_isi2)
p3 = figure(tools=TOOLS, plot_width=800, plot_height=300, title='信道长度为56',toolbar_location='left', toolbar_sticky=False)
p3.line(np.linspace(0, sig_exp.size-1, sig_exp.size),np.real(sig_exp), legend='sig_exp', line_color='red')
p3.line(np.linspace(0, sig_isi2.size-1-delay_rrc, sig_isi2.size-delay_rrc),np.real(sig_isi2[delay_rrc:]), legend='sig_isi-考虑滤波器延迟',line_color='green')fs = 1000  # 信道的采样频率
cir_sd3 = aup.arrivals_to_impulse_response(arrivals_sd, fs=fs)
cir_sd3 = np.real(cir_sd3)
cir_sd3[(cir_sd3 < 0)] *= -1  # 信道的冲激响应
sig_isi3 = np.convolve(cir_sd3, sig_tra)
sig_isi3 = nor(sig_isi3)
p4 = figure(tools=TOOLS, plot_width=800, plot_height=300, title='信道长度为110',toolbar_location='left', toolbar_sticky=False)
p4.line(np.linspace(0, sig_exp.size-1, sig_exp.size),np.real(sig_exp), legend='sig_exp', line_color='red')
p4.line(np.linspace(0, sig_isi3.size-1-delay_rrc, sig_isi3.size-delay_rrc),np.real(sig_isi3[delay_rrc:]), legend='sig_isi-考虑滤波器延迟',line_color='green')
show(p2)
show(p3)
show(p4)

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

为了方便观察，使用抽头长度为12的信道

3.3 接收端

接收方式：（做以下两种方式的测试）
（1）先滤波再均衡
（2）先均衡再滤波

M = int(cir_sd3.size)
mu = 0.0001
sig_rec1 = np.convolve(rrc, sig_isi3)
[sig_equ1, temp] = equlization(sig_rec1[delay_rrc*2:], sig_exp, mu, M)p5 = figure(tools=TOOLS, plot_width=800, plot_height=300,toolbar_location='above', toolbar_sticky=False)
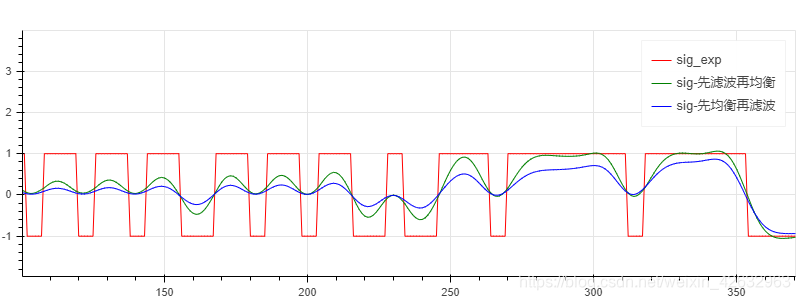
p5.line(np.linspace(0, sig_exp.size-1, sig_exp.size),np.real(sig_exp), legend='sig_exp', line_color='red')
p5.line(np.linspace(0, sig_equ1.size-1, sig_equ1.size),np.real(sig_equ1), legend='sig-先滤波再均衡',line_color='green')[sig_equ2, temp] = equlization(sig_isi3[delay_rrc:], sig_exp, mu, M)
sig_rec2 = np.convolve(sig_equ2, rrc)[delay_rrc:]
p5.line(np.linspace(0, sig_rec2.size-1, sig_rec2.size),np.real(sig_rec2), legend='sig-先均衡再滤波',line_color='blue')
show(p5)

在这里插入图片描述

3.4 判决并得到误码率

3.4 判决并得到误码率

1、只与原序列进行比较判决
2、在下采样之前就进行判决

def decision1(sig_ori, sig_res, sps):err = 0for i in range(sig_ori.size):if sig_res[i*sps+int(sps/2)] < 0:temp = -1else:temp = 1if temp != sig_ori[i]:err += 1return errdef decision2(sig_exp,sig_res):err = 0for i in range(sig_exp.size):if sig_res[i] < 0:temp = -1else:temp = 1if temp != sig_exp[i]:err  += 1return errprint(decision1(sig_ori,sig_equ1,sps)/N,decision1(sig_ori,sig_rec2,sps)/N)
print(decision2(sig_exp,sig_equ1)/N/sps,decision2(sig_ori,sig_rec2)/N/sps)

0.0298 0.0699
1.0 0.08368333333333333

在不同的采样频率下，得到的信道抽头个数就不同，具体均衡器的步长需要进一步设定。
经测试，调整步长的之后，误码率的结果还看的过去（比上面好看！）…

一花

第一次发博，关于Python、仿真或者其他地方有不好的地方，请批评我！！！

这篇关于水声多径信道下LMS仿真(Python代码)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/309984。

相关文章

Python版本信息获取方法详解与实战

Python版本信息获取方法详解与实战

《Python版本信息获取方法详解与实战》在Python开发中,获取Python版本号是调试、兼容性检查和版本控制的重要基础操作,本文详细介绍了如何使用sys和platform模块获取Python的主... 目录1. python版本号获取基础2. 使用sys模块获取版本信息2.1 sys模块概述2.1.1
阅读更多...
一文详解Python如何开发游戏

一文详解Python如何开发游戏

《一文详解Python如何开发游戏》Python是一种非常流行的编程语言,也可以用来开发游戏模组,：本文主要介绍Python如何开发游戏的相关资料,文中通过代码介绍的非常详细,需要的朋友可以参考下... 目录一、python简介二、Python 开发 2D 游戏的优劣势优势缺点三、Python 开发 3D
阅读更多...
Python函数作用域与闭包举例深度解析

Python函数作用域与闭包举例深度解析

《Python函数作用域与闭包举例深度解析》Python函数的作用域规则和闭包是编程中的关键概念,它们决定了变量的访问和生命周期,：本文主要介绍Python函数作用域与闭包的相关资料,文中通过代码... 目录1. 基础作用域访问示例1：访问全局变量示例2：访问外层函数变量2. 闭包基础示例3：简单闭包示例4
阅读更多...
Python实现字典转字符串的五种方法

Python实现字典转字符串的五种方法

《Python实现字典转字符串的五种方法》本文介绍了在Python中如何将字典数据结构转换为字符串格式的多种方法,首先可以通过内置的str()函数进行简单转换;其次利用ison.dumps()函数能够... 目录1、使用json模块的dumps方法：2、使用str方法：3、使用循环和字符串拼接：4、使用字符
阅读更多...
Python版本与package版本兼容性检查方法总结

Python版本与package版本兼容性检查方法总结

《Python版本与package版本兼容性检查方法总结》：本文主要介绍Python版本与package版本兼容性检查方法的相关资料,文中提供四种检查方法,分别是pip查询、conda管理、PyP... 目录引言为什么会出现兼容性问题方法一：用 pip 官方命令查询可用版本方法二：conda 管理包环境方法
阅读更多...
基于Python开发Windows自动更新控制工具

基于Python开发Windows自动更新控制工具

《基于Python开发Windows自动更新控制工具》在当今数字化时代,操作系统更新已成为计算机维护的重要组成部分,本文介绍一款基于Python和PyQt5的Windows自动更新控制工具,有需要的可... 目录设计原理与技术实现系统架构概述数学建模工具界面完整代码实现技术深度分析多层级控制理论服务层控制注
阅读更多...
pycharm跑python项目易出错的问题总结

pycharm跑python项目易出错的问题总结

《pycharm跑python项目易出错的问题总结》：本文主要介绍pycharm跑python项目易出错问题的相关资料,当你在PyCharm中运行Python程序时遇到报错,可以按照以下步骤进行排... 1. 一定不要在pycharm终端里面创建环境安装别人的项目子模块等，有可能出现的问题就是你不报错都安装
阅读更多...
Java集合之Iterator迭代器实现代码解析

Java集合之Iterator迭代器实现代码解析

《Java集合之Iterator迭代器实现代码解析》迭代器Iterator是Java集合框架中的一个核心接口,位于java.util包下,它定义了一种标准的元素访问机制,为各种集合类型提供了一种统一的... 目录一、什么是Iterator二、Iterator的核心方法三、基本使用示例四、Iterator的工
阅读更多...
Java 线程池+分布式实现代码

Java 线程池+分布式实现代码

《Java线程池+分布式实现代码》在Java开发中,池通过预先创建并管理一定数量的资源,避免频繁创建和销毁资源带来的性能开销,从而提高系统效率,：本文主要介绍Java线程池+分布式实现代码,需要... 目录1. 线程池1.1 自定义线程池实现1.1.1 线程池核心1.1.2 代码示例1.2 总结流程2. J
阅读更多...
Python打包成exe常用的四种方法小结

Python打包成exe常用的四种方法小结

《Python打包成exe常用的四种方法小结》本文主要介绍了Python打包成exe常用的四种方法,包括PyInstaller、cx_Freeze、Py2exe、Nuitka,文中通过示例代码介绍的非... 目录一.PyInstaller11.安装：2. PyInstaller常用参数下面是pyinstal
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2