本文主要是介绍ACWING/2004. 错字,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题解
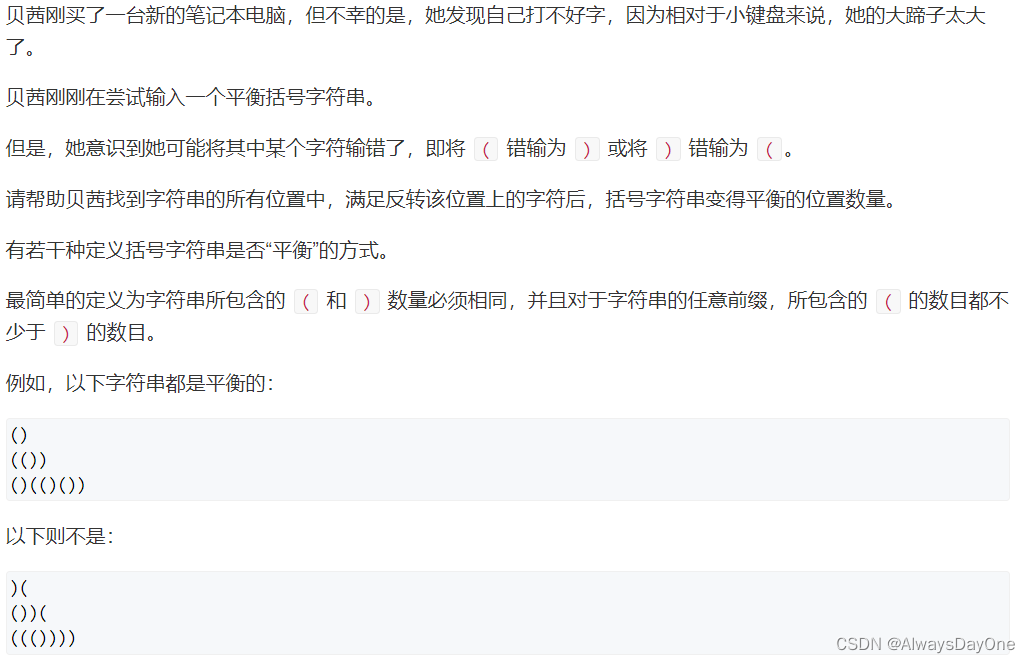
题目重点:
-
条件1:对于字符串的任意前缀,所包含的 ( 的数目都不少于 ) 的数目。
-
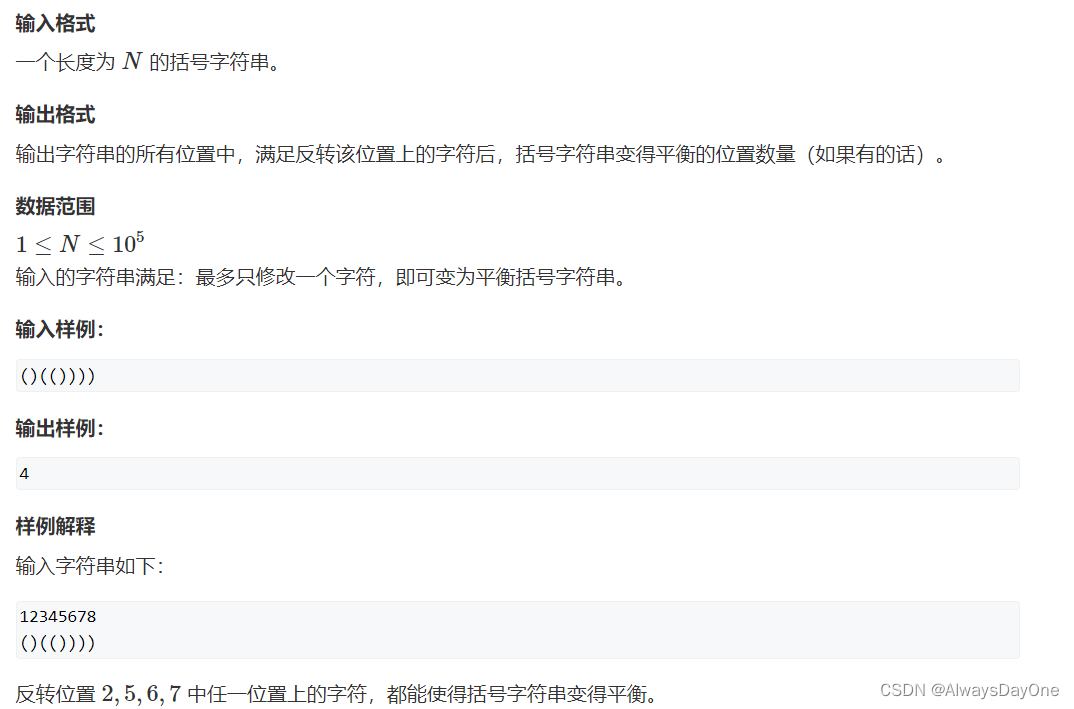
条件2:输入的字符串满足:最多只修改一个字符,即可变为平衡括号字符串。
因此本题限制在了只需要变化一个括号就一定能序列匹配!
结题思路:
-
分类:1.左右括号数R L相同;2.右括号需要转化为左括号:R=L+2;左括号需要转化为有括号:L=R+2
-
类型①:输出0直接
-
类型②:记录每个位置的从左到右 左右括号分别的前缀和,由条件1可得:从左向右搜索第一个左括号比右括号少的右括号位置, 则位置及其之前的任意一个右括号改变为左括号才能满足条件1,答案为此位置的右括号前缀和
-
类型③:记录每个位置的从右到左 左右括号分别的前缀和,由条件1可得:从右向左搜索第一个右括号比左括号少的左括号位置,则该位置及其右侧任意一个左括号改变为右括号就可以满足条件1,答案为此位置的左括号前缀和
#include <iostream>
#include <cstdio>
#include <cstring>using namespace std;int main(){string arr;cin>>arr;int n = arr.length();int L = 0,R = 0;for(int i = 0;i<n;i++){if(arr[i] == '(') L++;else R++;}int sumL[n+1] = {0}; // 前缀和int sumR[n+1] = {0};if(L == R){cout<<0<<endl;}else if(L < R){// 右括号需要转化为左括号:R=L+2for(int i = 0;i<n;i++){sumL[i+1] = sumL[i];sumR[i+1] = sumR[i];if(arr[i] == '(') sumL[i+1] = sumL[i+1] + 1;else sumR[i+1] = sumR[i+1] + 1;// 判断 第一个左括号比右括号少的右括号位置if(arr[i] == ')' and sumL[i+1] < sumR[i+1]){cout<<sumR[i+1]<<endl;break;}}}else{// 左括号需要转化为有括号:L=R+2for(int i = n-1;i>=0;i--){sumL[i] = sumL[i+1];sumR[i] = sumR[i+1];if(arr[i] == '(') sumL[i] = sumL[i] + 1;else sumR[i] = sumR[i] + 1;// 判断 第一个右括号比左括号少的左括号位置if(arr[i] == '(' and sumL[i] > sumR[i]){cout<<sumL[i]<<endl;break;}}}return 0;
}
这篇关于ACWING/2004. 错字的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








