关联分析中SPADE算法

目录

SPADE算法

例题讲解：

SPADE算法

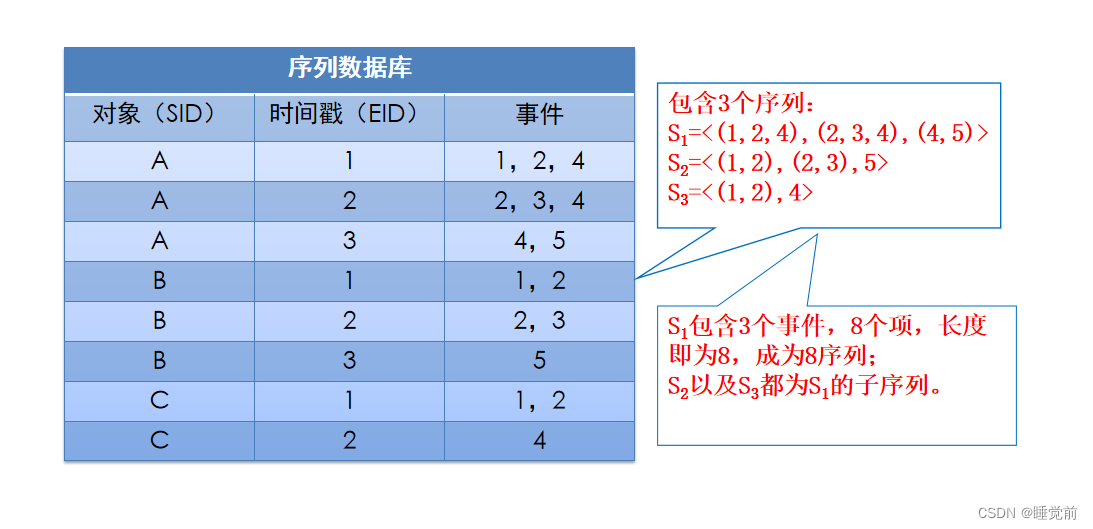
spade序列关联分析(时序关联分析)：即同一个对象在不同时间点对商品进行购买。

序列(sequence)数据库：序列数据库（sequence databases）S是包含一个或多个序列数据的数据集，是元组<SID，s>的集合，其中SID是序列编号，s是一个序列，每个序列由若干事件构成。

序列(sequence)：序列是事务的有序列表，可以记作s=<e1,e2,e3,…,el>，其中ej（1≤j≤l）表示事件，也称为s的元素；序列包含的项的数量记作序列的长度;

事件： 事件e是一个项集，可以记作e=（i1,i2,i3,…,in）；其中事件中的元素ij（1≤j≤n）表示项

子序列：设序列a= <a1a2…an>，序列b = <b1b2…bm>，ai 和bi都是元素。如果存在整数1 <= j1 < j2 <…< jn <= m，使得a1 包含于 bj1，a2 包含于 bj2，…， an  包含于 bjn则称序列a为序列b的子序列，又称序列a包含序列b，记为a 包含于b。

举例说明：

例如序列<{2}，{1，3}>是序列<{1，2}，{5}，{1，3，4}>的子序列，因为{2}包含在{1，2}中，{1，3}包含在{1，3，4}中。

而<{2，5}，{3}>不是序列<{1，2}，{5}，{1，3，4}>的子序列，因为前者中项2和项5是一次购买的，而后者中项2和项5是先后购买的，这就是区别所在。

定义（前缀） 前缀形式化定义如下：定义一个函数p：(S，N)→S，其中S是一个序列集合，N是一个非负整数，p(X，k)=X[1:k]，换句话说，p(X，k)返回X的k长度的前缀。 在序列格S上定义一个等价关系如下：X，Y∈S，当且仅当p(X，k)=p(Y，k)，也就是说这两个序列共享长度为k的前缀，则它们是θk等价的，记为 。由X构成的等价类记为 。

在该序列格上由θ1导出的等价类集合是{[A]，[B]，[D]，[F]}，称这些第一层的类为父类，在图中下方。可以看到，所有具有共同前缀的序列被划分到同一等价类中，每个等价类都是序列格的一个子格。 

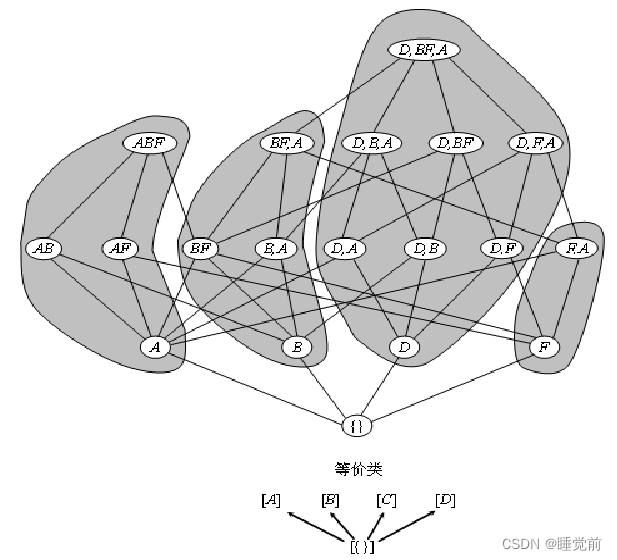
    只有同一个类中的两个k-序列才能进行时态连接运算，并产生长度为(k+1)的候选序列。 因此，为了产生所有(k+1)-序列，仅需要在每个前缀等价类中执行一个简单的时态连接即可，而这种连接可被独立处理。

根据被连接的原子类型，可得3种可能的频繁序列：

1.两个事件原子项连接：<AB>和<AC>进行连接得到<ABC>。

2.事件原子项与序列原子项之间连接：<AB>和<A，C>进行连接得到<AB，C>。

3.序列原子项与序列原子项之间连接：<A，B>与<A，C>进行连接得到<A，BC>、<A，B，C>或<A，C，B>。

一个特殊的情况是，当对<A，B>进行自连接时，则只能产生唯一的新序列<A，B，B>。

 下面举例说明：

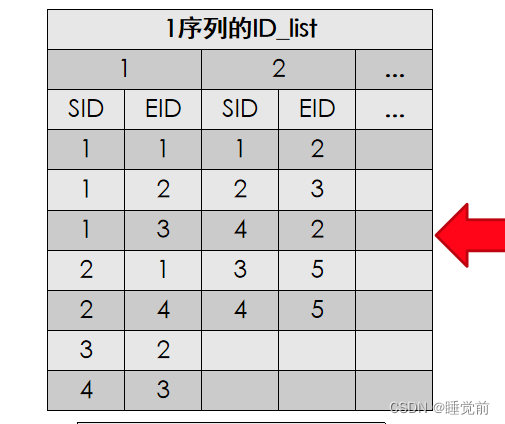
水平数据格式转换为垂直数据格式，1序列的ID_list就是含有项集1，项集2......到最后的SID和EID

（购买人和时间点）

2序列的ID_list就项集1，2，3，4，5，6的两两交集（1，2）（1，3）（2，3）........到最后的SID和EID（购买人和时间点）

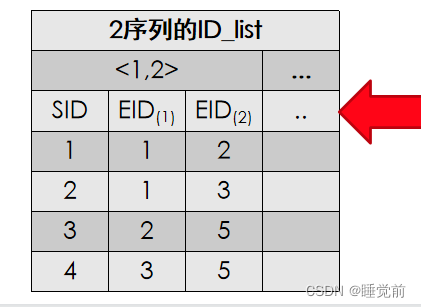
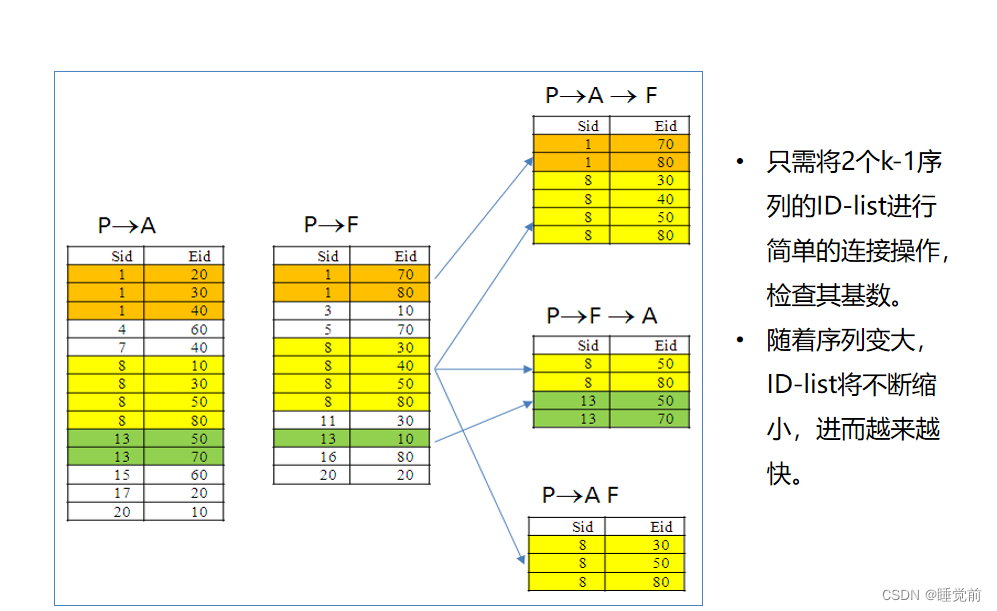
    以上怎么理解呢，就是说如果P->A->F得到的一定是F中大于A的SID和EID，也就是A要包含于F（这里的包含是指一个事件的包含，不是全部都要包含，满足一个即可），所以P->F->A中F要包含于A，则A中只有（8，50）（8，80）满足。P-AF就是AF相交。

以下是序列D->BF->A的实现过程。

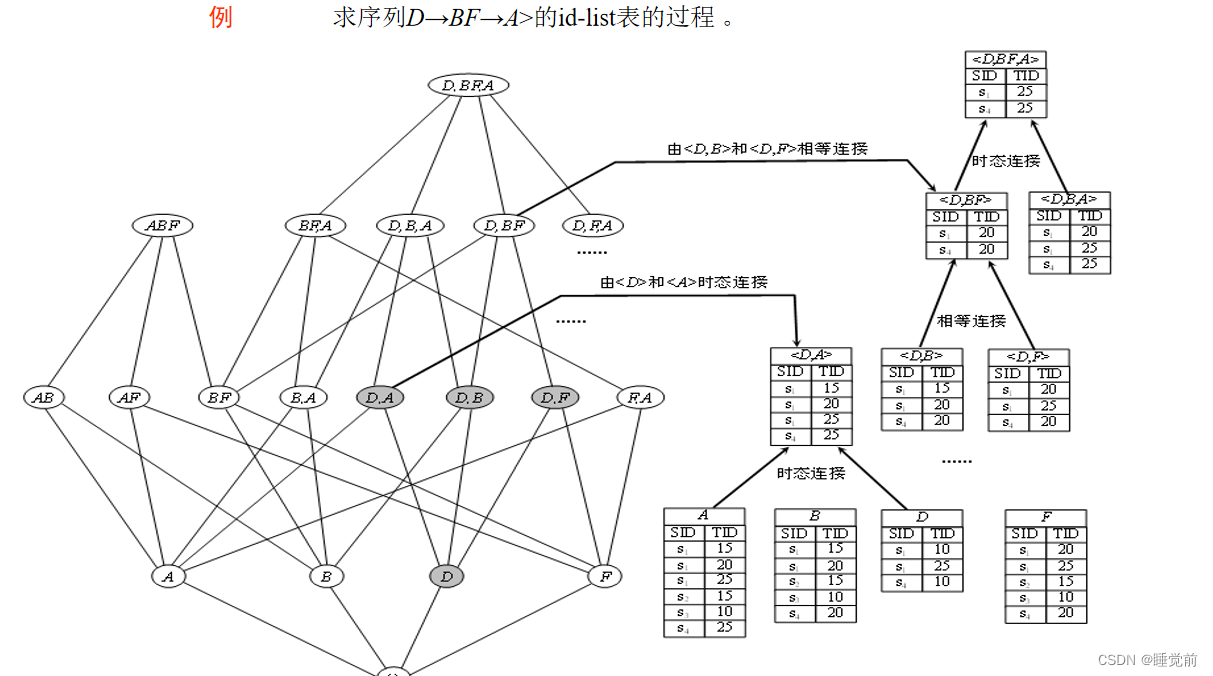
例题讲解：