HDU - Segment Tree with Pruning

题目链接：https://acm.hdu.edu.cn/showproblem.php?pid=6983

Problem Description
Chenjb is struggling with data stucture now. He is trying to solve a problem using segment tree. Chenjb is a freshman in programming contest, and he wrote down the following C/C++ code and ran ‘‘Node* root = build(1, n)’’ to build a standard segment tree on range [1,n]:

Node* build(long long l, long long r) {
Node* x = new(Node);
if (l == r) return x;
long long mid = (l + r) / 2;
x -> lchild = build(l, mid);
x -> rchild = build(mid + 1, r);
return x;
}

Chenjb submitted his code, but unfortunately, got MLE (Memory Limit Exceeded). Soon Chenjb realized that his program will new a large quantity of nodes, and he decided to reduce the number of nodes by pruning:

Node* build(long long l, long long r) {
Node* x = new(Node);
if (r - l + 1 <= k) return x;
long long mid = (l + r) / 2;
x -> lchild = build(l, mid);
x -> rchild = build(mid + 1, r);
return x;
}

You know, Chenjb is a freshman, so he will try different values of k to find the optimal one. You will be given the values of n and k, please tell him the number of nodes that will be generated by his new program.

Input
The first line contains a single integer $T(1\le T\le 10000)$, the number of test cases. For each test case:

The only line contains two integers n and k $(1\le k\le n\le 1e18)$, denoting a query.

Output
For each query, print a single line containing an integer, denoting the number of segment tree nodes.

Sample Input
3
100000 1
100000 50
1000000000000000000 1

Sample Output
199999
4095
1999999999999999999

题目大意：
给定整数区间[1,n]和一个整数k，判断题目给定的第二段代码由该区间生成的对应的树有多少个节点

思路：
首先题目生成这棵树的过程可以稍微转化一下，我们只需要区间的长度，而不需要区间的两界。根据代码逻辑，也就是，给定区间长度为n，最终会生成一颗叶子节点对应长度不超过k的总共有若干个节点树。对于每一个节点的区间长度r，如果r大于k，那么它必不是叶子节点，那么它会连接有两个子节点。
当r为奇数时，其连接的左节点长度为 $r/2+1$，右节点长度为 $r/2$，如果是偶数，则长度都为 $r/2$.

我们可以修改一下其给定的代码，从而以$O(logn)$效率得到其生成出来的树所达到的最大深度。当其深度为D时，对于其1~D-1的所有层，必然都是满的，而D层则未知。
我们假定一个小于n的整数P，其生成出来的树恰好是具有D-1层的完全二叉树，并且叶子节点长度都为k。当我们将P，逐渐+1，在其+1的过程中，会发现一个规律：对于一个节点，每次加入一个1，这个1都会自上而下将其 “区间长度最小的、最靠左的”对应子节点+1。如下图：

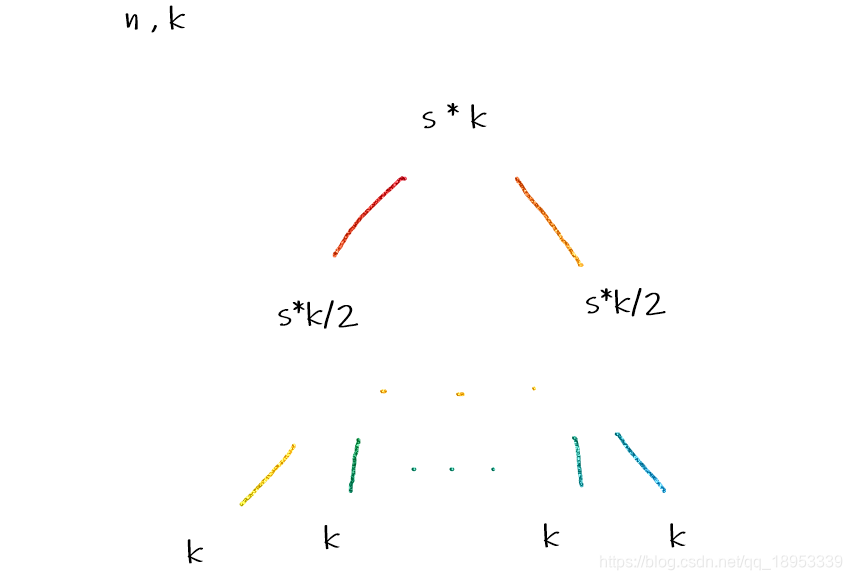
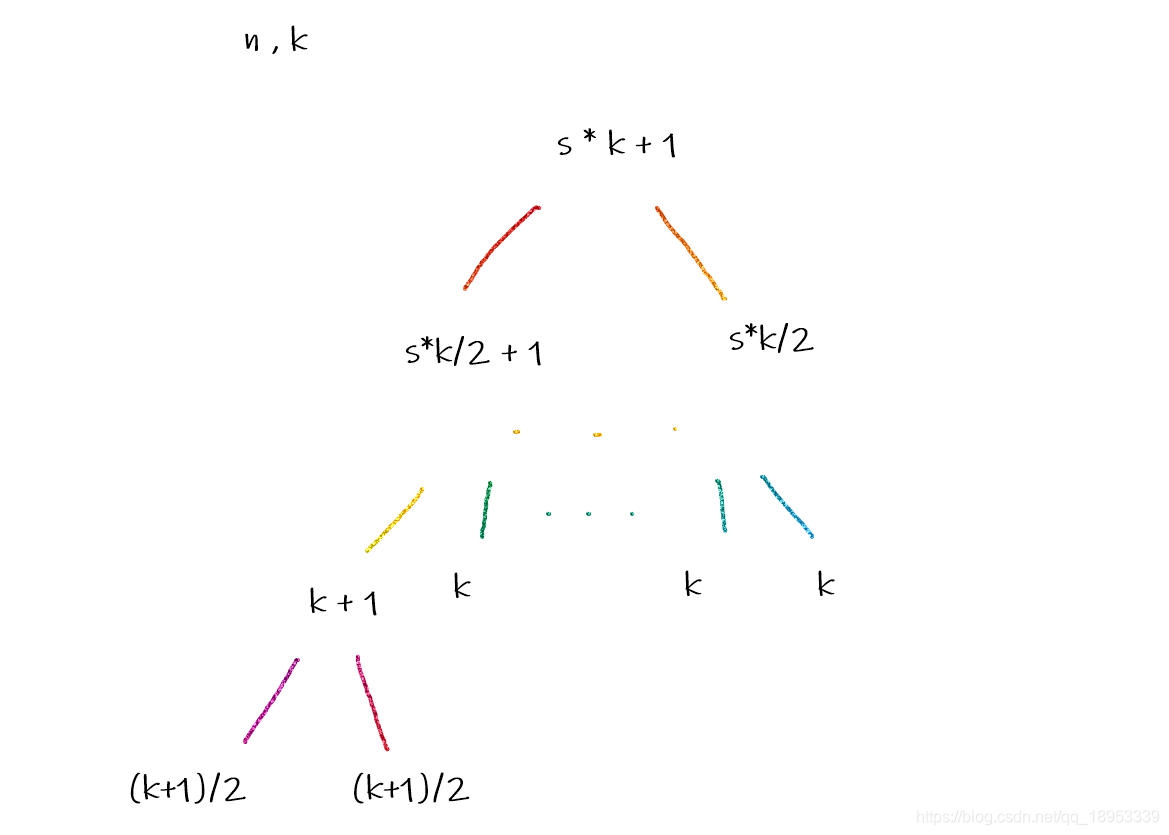
原本叶子节点都是所能取的最大长度k，而+1之后，超过了这个值，那么就会衍生出两个叶子节点。
而这样的+1操作，我们需要执行n-P次，我们如何确定最后的结果？

我们需要统计，P的时候，其叶子节点有几个，当我们要执行的操作小于等于这个初叶子节点数时（假设为V个吧），我们最终会增加2V个叶子节点（每次操作都会衍生两个），而当我们进行的操作大于这个V时，则至多也只能增加2V个叶子节点，因为后续的操作只是在“填充”现有叶子节点的长度罢了，却不可能再使其超过给定k了（因为我们一开始就求得其最大深度为D了呀，如果还能超过，说明我们D求的不对）。这样我们就能通过预处理不同层数满时该层对应的节点数目与不同层数的满二叉树节点数，比较快速地求出所有样例对应的结果。（一开始因为直接用pow()求对应的2的高次幂前缀和时产生了一些未知问题，数据大于一定范围的时候，其求出结果比实际结果大1，也导致了比赛时最终没能写出这道题）

AC代码：

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
long long n, k;
long long ci[1000006];
long long deep(long long l, long long r) {if (r - l + 1 <= k)return 1;return deep(l, (l + r) / 2) + 1;
}
int main(void) {ci[1] = 1;long long it = 2;for (int i = 2; i <= 64; i++) {ci[i] += ci[i - 1] + it;it *= 2;}long long t; cin >> t;while (t--) {cin >> n >> k;if (n <= k) {cout << 1 << endl; continue;}long long Deep = deep(1, n);long long now = ci[Deep - 1];long long temp = (long long)pow(2, Deep - 2);long long yu = n - temp * k;now += min(temp * 2, yu * 2);cout << now << endl;}
}