【安全与风险】普适计算中的安全与隐私研究

日常生活的数字化

数字足迹是你在使用互联网时创建的数据痕迹。它包括你访问的网站，你发送的电子邮件，以及你提交给在线服务的信息。

1. “被动数字足迹”是指你无意中在网上留下的数据痕迹。
   1）当您访问某个网站时，web服务器可能会记录您的IP地址，从而确定您的大致位置。
   2）搜索历史记录，在您登录时由某些搜索引擎保存。
2. “活跃的数字足迹”包括您有意在线提交的数据。
   纳税情况:个人资料、电话号码、地址……

无处不在的计算对移动社交媒体的影响

1. 发布博客和发布社交媒体更新是扩大你的数字足迹的其他流行方法。
2. 你在推特上发布的每一条推文，你在脸书上发布的每一次状态更新，以及你在Instagram上分享的每一张照片，都对你的数字足迹有贡献。你在社交网站上花的时间越多，你的数字足迹就越大。
3. 甚至“点赞”一个页面或Facebook帖子都会增加你的数字足迹，因为这些数据保存在Facebook的服务器上。

讨论

列出你每天与移动设备的互动，并讨论你的安全和隐私风险。

1. 电子邮件
2. 电子商务
3. 移动应用程序
4. 移动支付
5. 社交网络

更便宜的存储和更强大的处理的影响

1. 廉价和先进的存储容量
   1）存储更多(无论当前阶段是否有用)
   2）数据黑市
2. 强大计算能力
   多核、分布式计算/云计算
3. 对手拥有更多资源

移动和普适计算的影响

事物都有两面性:

1. 连续传感(时间、位置)
   位置隐私，时间数据分析…
2. 多模态(多方面实现融合)
3. 感觉的隐形(无意识)
4. 协作本质
   连接或遇到其他ubicomp(普适计算)/移动设备

有时候，惊奇

1. 一种新的侧信道攻击，利用智能手机的加速度计来窃听同一智能手机的扬声器。
2. 具体来说，它利用加速度计的测量来识别说话者发出的语音，并重建相应的音频信号。
3. 我们通常不知道这些…

加速度计可以被劫持，对智能手机扬声器引起的振动进行采样。然后，攻击者使用信号处理和人工智能将信号转换为语音。

另一个例子

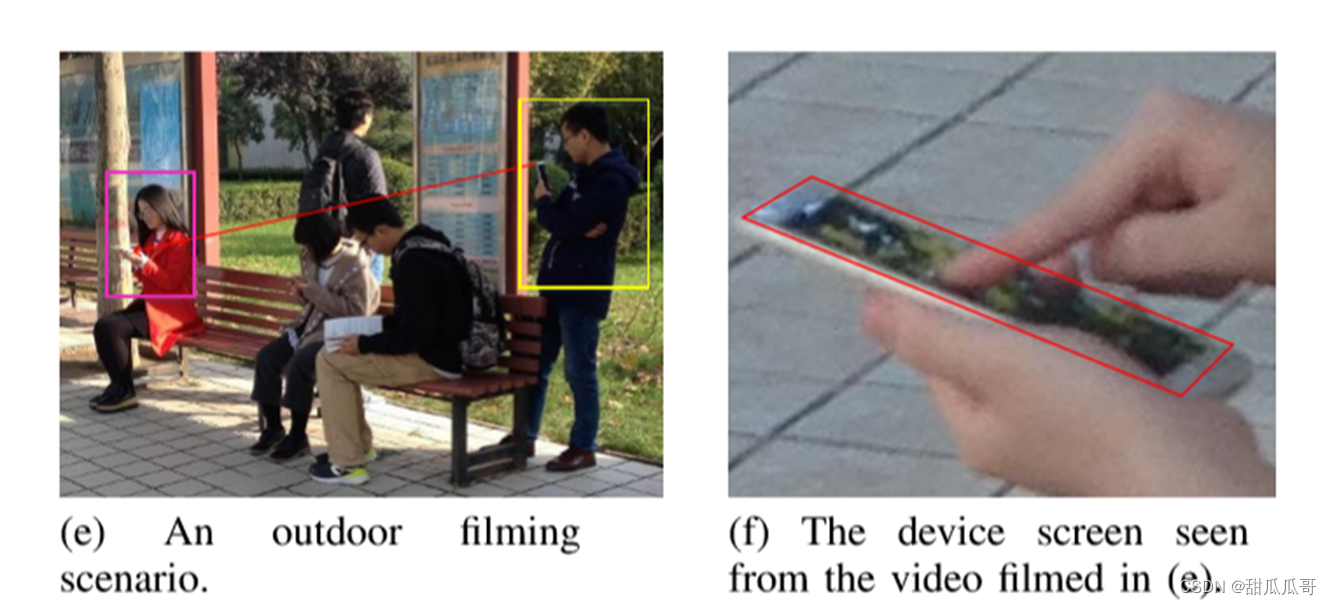
攻击模型

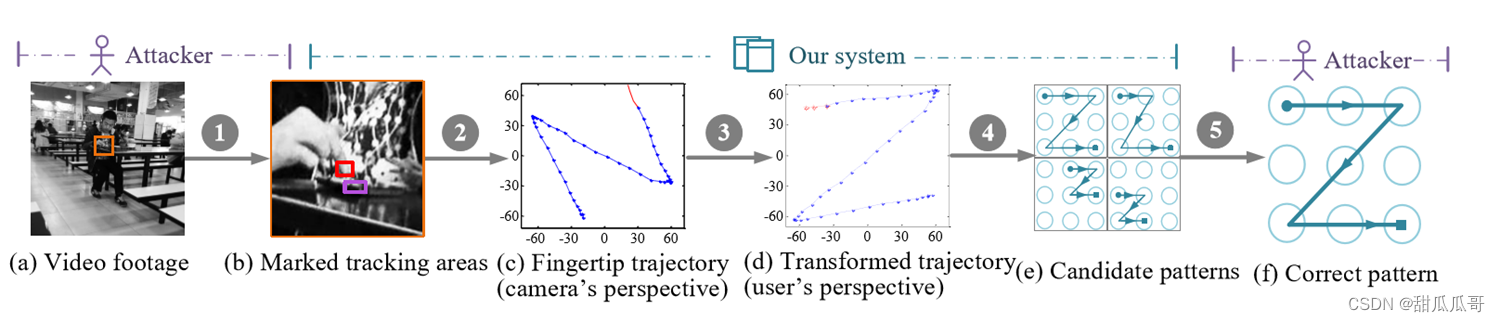
贡献是什么？

1. 新的进攻（五步攻击模型）
2. 最新漏洞
   许多用户可能低估了在公共场所使用图案锁的危险。在攻击下，拍摄可以在距离用户2米的距离内进行，摄像机不需要直接面对目标设备。
3. 新发现
   说明在基于视频的攻击下，复杂的模式更容易受到攻击。这一发现推翻了许多人的观念，即更复杂的模式提供更强的保护。
   提供关于模式锁实际使用的新见解。

基于视频的Android模式锁定攻击
复杂的图案提供了更多的保护，防止直接观察技术(例如，肩部冲浪)。然而，它们独特的图形结构帮助论文中使用的算法缩小了可能的选择范围。所提出的系统为所有采样的复杂模式产生一个候选模式——在大多数情况下是正确的。

智能家居的案例研究

Yang, Longqi, Kevin Ting, and Mani B. Srivastava. “Inferring occupancy from opportunistically available sensor data.” 2014 IEEE International Conference on Pervasive Computing and Communications (PerCom). IEEE, 2014. (Best Runner-up Paper Award)

本文的主要内容

商业和住宅建筑通常配备仪表和传感器，这些仪表和传感器作为公用事业基础设施的一部分部署，由提供电、水、气、安全、电话等服务的公司安装。

这些服务提供商可以直接访问来自传感器和仪表的信息。一个值得关注的问题是，供应商收集的感官信息虽然是粗粒度的，但可以进行分析，从而揭示有关建筑物用户的私人信息。

通常，同一家公司提供多种服务，在这种情况下，私人信息泄露的可能性增加了。

本研究旨在调查在多大程度上容易获得的感官信息可能被外部服务提供者用来做出与占用有关的推论。

他们特别关注两个不同来源的推论：

1. 运动传感器(由保安公司安装和监控)
2. 智能电表(由电力公司部署计费)

他们探索了一个基于三人独户家庭的运动传感器场景，以及一个基于12人大学实验室的电表场景。

本文表明，服务提供商可以获得的感官信息可以使他们做出不希望的占用相关推断，例如确定占用水平，甚至发现当前占用者的身份

如何自学?

自学步骤：

1. X是什么?
2. X的安全研究问题有哪些
3. 主要方法或影响
4. 阅读一篇论文作为案例研究

Acknowledgements: Jiangtao Wang