本文主要是介绍数据结构—并查集UnionFind,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原文作者:愚公要移山1
原文地址:一个非常实用而且精妙的算法-并查集(java语言实现)
在学习数据结构的时候,老师多少会提到并查集,他的应用也是超级广泛。本文首先会通过案例来对并查集有一个介绍。然后给出并查集的java实现。
1、并查集原理
话说在江湖上有很多门派,这些门派相互争夺武林霸主。毕竟是江湖中人,两个人见面一言不合就开干。但是打归打,总是要判断一下是不是自己人,免得误伤。
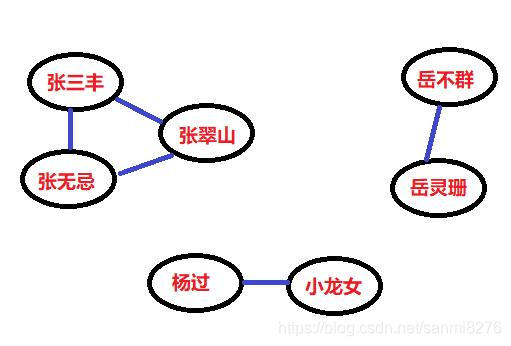
于是乎,分了各种各样的门派,比如说张无忌和杨过俩人要打架,就先看看是不是同一门派的,不是的话那就再开干。要是张无忌和杨过觉得俩人合得来,那就合并门派。而且规定了,每一个门派都有一个掌门人,比如武当派就是张三丰。华山派就是岳不群等等。现在我们把目光转到并查集上。
- 张无忌和杨过打架之前,先判断是否是同一门派,这就涉及到了并查集的查找操作。
- 张无忌和杨过觉得俩人合得来,那就合并门派,这就涉及到了并查集的合并操作。
- 每一个门派都有一个掌门人,这涉及到了并查集的存储方式。掌门人代表了这个门派的根节点。
现在我们从这个例子的思想开始认识一下并查集。
2、并查集简单实现
并查集主要涉及到两种操作,合并和查找。假设有一个动态集合:S={s1,s2,s3,…..sn}。在这个集合里面每一个元素都是一个江湖人物。比如S1代表了岳不群等等。我们实现一个并查集的时候首先要考虑的就是存储结构,一般情况下有两种:数组和链表。现在我们使用数组来实现一下。
1)类架构
// 并查集模板
class UnionFind {//使用数组存储每一个英雄的上级领导int[] s;//记录江湖中英雄的数量int count;//构造函数,负责初始化并查集public UnionFind(int n) {}//合并操作public void unite(int root1, int root2) {}//查找操作public int find(int x) {}
}
在上面的类中,我们只是定义了一个雏形,还没有给出一个具体的实现。下面我们针对并查集的查找和合并操作。给出以下具体的实现。在这里数组s中存储了每一个江湖人的上级。比如说 s[i] 表示该元素 i 的上级领导。
2)构造函数
在前文的例子中,我们规定了每一个门派都有一个掌门人。但是在江湖开始的时候,每个人都是自成一派的,也就是每一个江湖人的上级都是他自己。在这个构造函数里面,首先初始化了一个数组s,然后赋值numElements给count,接下来使用for循环,初始化每一个江湖人的上级都是他自己,在这里使用-1表示。
//构造函数,负责初始化并查集
public UnionFind(int n) {this.s= new int[n];this.count = n;//一开始每个人都自成一派for (int i = 0; i < n; i++) {//每一个英雄的上级都是自己s[i] = -1;}
}3)合并操作
Union操作就是将两个不相交的子集合合并成一个大集合。如何去合并呢?其实原理很简单,只需要把一棵子树的根结点指向另一棵子树即可完成合并。也就是指定其中一个人是另外一个人的上级就好了。就这一行代码就可以实现合并,但是这个方式虽然简单,但是肯定是存在着很多问题,一会再说。
//合并操作
public void unite(int root1, int root2) {//将root1作为root2的根s[root2] = root1;
}4)查找操作
Find操作就是查找某个元素所在的集合,返回该集合的代表元素。通俗的理解就是根据张无忌找到其相应门派的掌门人张三丰。到目前为止,我们可算是把并查集的基本实现都给完成了,但是前文中不是提到了嘛,合并的时候其实是有很多问题,而且查找的时候依然也有很多问题。别着急,想要我们的算法更加的高效,就必须要好好地改进一波。
//查找操作
public int find(int x) {//如果说s[x]<0,也就是为-1,说明当前的x为门派的根if(s[x]<0)返回门派的根,也就是掌门人return x;else//否则的话,递归查找即可find(s[x]);
}
3、并查集改进
1)出现问题
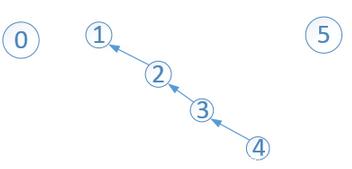
上面介绍的Union操作很随意:任选一棵子树,将另一棵子树的根指向它即完成了合并。也就是随意指定一个人成为另外一个人的上级。合并操作越来越多的时候,可能会出现一个非常不平衡的情况。这就是不好的现象,而且我们想要查找节点4的根节点,就需要4-->3-->2-->1一直不停的找,这效率真的很恶心。
2)合并操作改进
合并的时候,判断一下root1和root2谁的子节点多,谁多谁做上级领导。就好比是两个人见面合并,谁的人数,谁做大哥。
//合并操作
public void unite(int root1, int root2) {if(find(root1)==find(root2)return;//如果root2的人多,那就用root2做大哥if(s[root2] <= s[root1])s[root1] = root2;//每次合并,江湖上都会少一个人count--;
}
2、查找操作改进
在查找的时候,将这条路上的所有节点,全部让掌门人直接管理。这很明显改变了树的高度。
//查找操作
public int find(int x) {//如果说s[x]<0,也就是为-1,说明当前的x为门派的根if(s[x]<0)返回门派的根,也就是掌门人return x;else//使用了路径压缩,让这条路径上的所有人的上级直接变为掌门人return s[x] = find(s[x]);//return s[x] = find(s[x]);
}
OK,并查集的基本操作就是这样。面试的时候经常会有并查集相关的题目。我总结了一部分。大概十几道题,都是力扣上的。
这篇关于数据结构—并查集UnionFind的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






