本文主要是介绍“泰迪杯”挑战赛 - 通过数据挖掘预测肝癌手术治疗效果,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目 录
- 研究目标
- 分析方法与过程
2.1. 总体流程
2.2. 具体步骤
2.3. 结果分析 - 结论
- 参考文献
1. 挖掘目标
本次建模主要针对某医院 10 年来肝癌病例中的 20 个有代表性的样本,选取对预后有影响的 l0个指标进行统计分析;以预后影响作为评价标准,建立数据挖掘模型,实现对手术的治疗效果的自动分类和方案的优劣进行预测,从而为病人规划最佳的手术和治疗方案。
2. 分析方法与过程
2.1. 总体流程
为了让建模更为清晰,结合该 20 个样本的特点,我们建模的主要步骤如下:
一、 针对本数据集的特点,对该样本进行简单的描述性统计,并设计出指标变量;
二、 基于逻辑回归模型的统计建模,实现对手术的治疗效果的自动分类和方案的优劣进行预测,并对模型结果给出合理的解释;
三、 利用逐步回归思想改进逻辑回归模型,并进行两个模型进行比较模型优良。
四、 基于 ROC 曲线比较以上两种分类器的性能,给出最优模型。

2.2. 具体步骤
2.2.1 数据介绍
在详细介绍建模之前,我们给出数据集如下



这里一共有 10 个变量指标,其中 X1 到 X10 为解释变量,DECISION 为被解释变量。在这里除了X6 可以转化为数值型变量外,其余都是定性变量指标,我们不能使用简单的回归进行建模,必须考虑定性变量的性质。从以上表中可以看到,这 20 个样本中 9 个预后有影响、11 个预后没有影响的样本,为了更清晰明了地了解预后影响和其它变量的关系,我们需要进行初步的描述性统计分析。
2.2.2 描述性统计
本建模应该考虑哪些指标变量呢?换句话说,哪些解释变量会对被解释变量 DECISION 有较大影响呢?如何对 X1 到 X10 这些变量进行预处理,以转化为可分析的指标变量?以下我们以预后影响DECISION 为 Y 时设计为 1,为 N 时设计为 0 来表识是否有预后影响。并以此为因变量对各解释变量进行描述性统计,以便找出各解释变量的进一步转化。
1.食道静脉曲张(X1)

那么该如何解读解读这个表格呢?就拿第二列来说吧,7 表示 20 个样本中有 7 个样本 X1 变量的值是 no,其中 7 个 X1 变量的值为 no 的样本中有约 29%是预后有影响的,其余的可以类似的来解释。但是我们发现有轻微的食道静脉曲张的样本中,预后有影响的占较大比例,这也超过中度以及严重程度时的比例,这也许是样本量太少造成的误差,为此我们可以考虑对 X1 有无食道静脉曲张来进行分类,重新统计,我们可得有食道静脉曲张的样本量为 13 个,其中有 7 个对预后有影响,占比为 54%,这远大于没有食道静脉曲张的 29%。从数据出发,我们可得,没有食道静脉曲张的患者具有更好的预后效果。
2.门脉癌栓(X2)

从上表可以看出,门脉癌栓在三个不同属性下对预后影响的比例并没有显著性差异,但由于在临床实践中发现,肝癌门静脉栓的形成是影响肝癌预后的重要因素,临床发生率高达 60%-90%,可 惜的是迄今为止肝癌门静脉栓形成的原因尚不明确。
3.HbsAg(X3)与 Anti-HCV (X4)

阳性 HbsAg 相对于阴性 HbsAg 对预后影响具有显著差异性,而且从表中可以看出,相比于阴性HbsAg,阳性 HbsAg 且预后有影响占有更大的比例,这说明 HbsAg 为阴性的肝癌患者具有更好的预后效果。同样 Anti-HCV 的阳性和阴性也对预后的影响有很大不同,这个差异也是相对明显的,可以看出这个变量很大可能对预后具有较大影响,同时可见 Anti-HCV 阳性患者的预后效果相比于阴性患者的效果更好。可惜的是,Anti-HCV 的阳性,即丙性肝炎病毒抗体阳性说明患者曾经感染或者正在感染丙型肝炎,这对预后会有不良影响,这也许是数据量太少,造成这种统计上的偏差。在考虑建模时需要特别注意该变量。
4.肿瘤部位(X5)
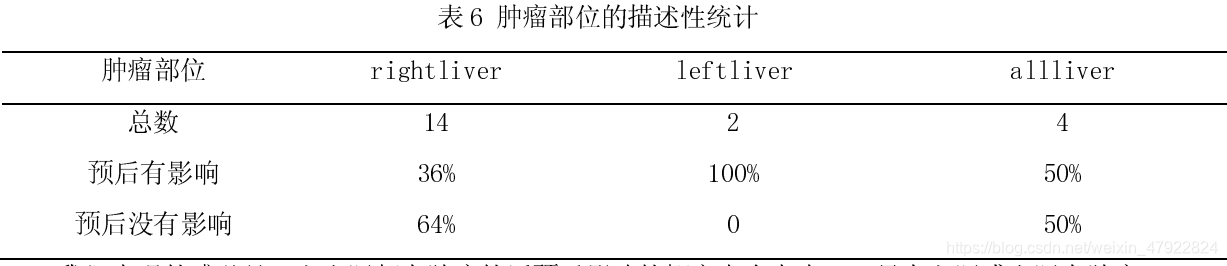
我们直观的感觉是,左右肝都有肿瘤的话预后影响的概率也会大点,而只有左肝或右肝有肿瘤预后有影响应该会更小,经过再次统计,我们也发现发现左右肝都有肿瘤的对预后有影响(50%)比 只有左肝或右肝有影响(0.44)稍大。
5.肿瘤大小(X6)

从初步数据看来,肿瘤大小对预后影响并没有很明显的结论,有可能这是一个并不是很重要的指标,其影响相对较小。由于这个变量是具有数值上意义的,我们可以用它们的中位数或者平均值 代替其各水平的值,直径<3cm(small)、35cm(middle)、510cm(big)、>10cm(verybig)分别用 x6 等于 1.5、47.5 以及 10 来数值化该变量。
6.肿瘤生长方式(X7)与肿瘤的包膜(X8)

从肿瘤生长方式可以看出,浸润和膨胀两者的总数相同,而却两者中预后有影响的比例相差不大。膨胀性生长,肿瘤向周围扩散,挤压周围组织或邻近器官。周围可形成纤维性包膜。浸润性生 长,瘤细胞沿组织间隙或毛细淋巴管扩展。一般而言,浸润式生长的肿瘤会更恶性。但对于肿瘤的包膜而言,肿瘤的包膜是完整的样本中,预后有影响所占的比例(14%)远小于其他两种情况。
7.肿瘤旁的微小子灶(X9)与术后腹水(X10)

从肿瘤旁的微小子灶上看,有微小子灶的患者明显比有微小子灶的患者预后好,这与我们的经 验有冲突,作为预测的话,我们需要特别注意这个变量。而术后是否有腹水方面来看,没有腹水的患者更倾向于具有预后影响。
2.2.3 指标设计
在描述分析的基础上,我们对模型中需要用的的指标重新设计,具体如下表:

2.2.4 统计模型
虽然描述性统计能在一定程度上给我们一些信息,但是由于我们考虑的时候都是单独考虑的, 并没从整体出发,忽略了各变量之间的相关关系,这难免会造成不准确,所以我们仍然需要进行系统的统计建模,把所有的变量放在一起考虑,以降低分析的失误。
在指标设计以及描述统计的基础上,讨论如何建立回归模型。我们关心的问题是,哪些指标可能影响预后影响。由于我们希望根据各解释变量的情况预测出最后的预后是否有影响,这是一个很经典的分类问题。对于这一分类问题的建模,我们可以采用贝叶斯分类、决策树分类、随机森林法、支持向量机以及逻辑回归,它们各有各的优缺点,在这里我们主要给出逻辑回归模型,并基于这一模型给出相应的结论。
逻辑回归分析是用来处理分类问题的一种统计建模方法,我们可以建立如下的逻辑回归模型:
p ( X ′ β ) = e X ′ β 1 + e X ′ β p(X' \beta)=\frac{e^{X' \beta}}{1+e^{X' \beta}} p(X′β)=1+eX′βeX′β
或者等价地有
l o g i t { p ( X ′ β ) } = l o g { p ( X ′ β ) 1 − p ( X ′ β ) } = X ′ β logit\{ p(X' \beta)\}=log\{ \frac{p(X' \beta)}{1-p(X' \beta)} \}=X' \beta logit{p(X′β)}=log{1−p(X′β)p(X′β)}=X′β
这里
X ′ β = β 0 + β 1 X 1 + β 21 X 21 + β 22 X 22 + β 3 X 3 + . . . . + β 10 X 10 X' \beta=\beta_0+\beta_1X_1+\beta_{21}X_{21}+\beta_{22}X_{22}+\beta_3X_3+....+\beta_{10}X_{10} X′β=β0+β1X1+β21X21+β22X22+β3X3+....+β10X10
这就是我们需要建立的逻辑回归模型。
同普通线性回归模型相似,对于逻辑回归而言,人们关心回归系数 β 。对于一个给定的变量 X j X_j Xj , β j = 0 β _j = 0 βj=0 意味着在给定其他解释变量不变的前提下,该指标对于解释条件概率 p ( X ′ β ) p (X'β) p(X′β) 没有任何帮助。因此对于解释因变量 Y 的随机行为也没有任何帮助。但是,如果 β j > 0 β_j > 0 βj>0 ,那么在给定其他解释变量不变的前提下,指标 X j 的上升会带来条件概率 p ( X ′ β ) p (X'β) p(X′β)的下降,也就是说,因变量取值为 0 的可能性会变大。从某种角度看来,这似乎是一种“负相关”。
考虑到变量间的共线性影响,而且并不一定所有的变量对因变量都有很好的解释作用,为了进一步优化模型,我们考虑选择逐步回归的方法进行变量选择,再次进行逻辑回归得到我们的结果。 为此如下给出全模型以及优化模型的结果,并比较其作为分类器的优劣。
2.3. 结果分析
2.3.1 模型结果
有了以上的理论基础,我们采用 R 统计软件使用逻辑回归进行编程,运行得到各参数估计如下:
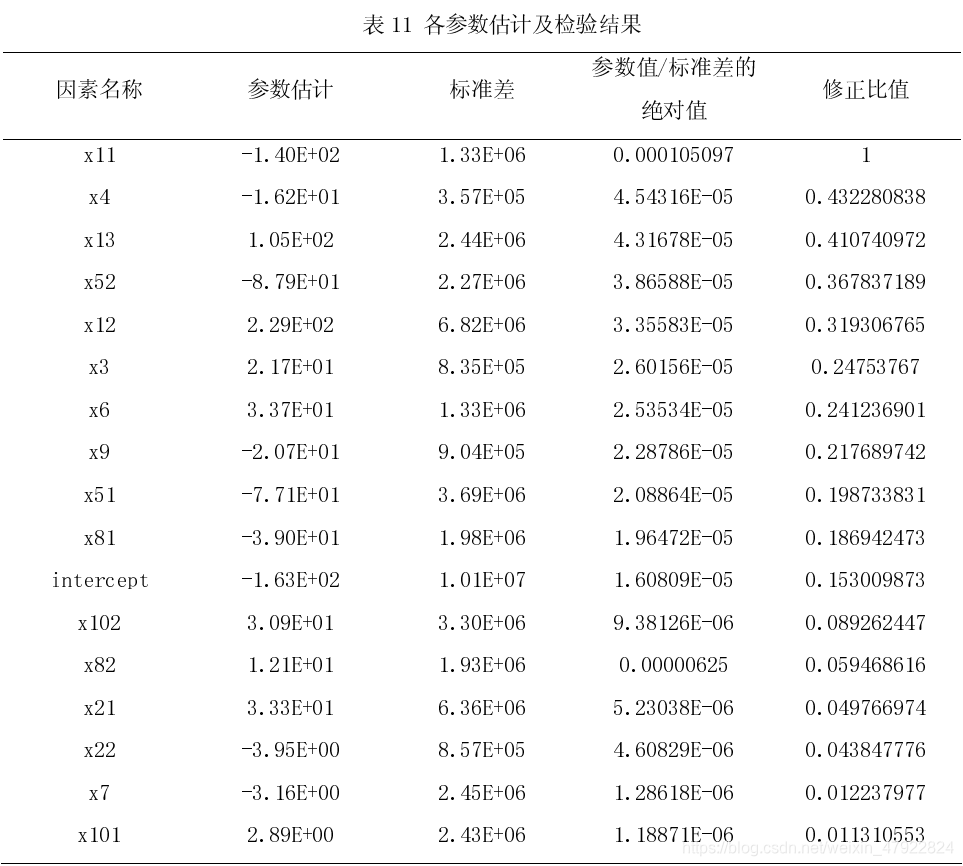
此表中第四列为参数估计值和标准差的比值的绝对值,这个值越大意味着参数取值为非 0 的可能性就越大,从某种程度上说是变量重要程度的一种度量,为了更清晰地对这个比值大大小进行观察,我们给出它们相对于最大值的一个修正比值,并将其在图表中展示出来。此表是按照修正比值从大到小进行了排列,从这个排列我们可以得出:食道静脉曲张、Anti-HCV 以及 HbsAg 是否阳性、肿瘤位置、肿瘤大小、肿瘤的包膜是否完整等都对分类器具有很大的影响。其中若变量前面的系数 为正数,说明具有该特征具有更大可能性的预后影响,相反地,变量系数为负说明具有该特征能够降低预后的影响。
我们拿食道静脉曲张来说,x11 是负值,x12 和 x13 都是正值,说明没有食道静脉曲张的患者比有(哪怕是轻微程度)曲张的患者预后效果会更好,也就是说预后没有影响的可能性更大。x51和 x52(整个肝脏的系数是 0)的值都是负值,这说明单单只有左肝或者右肝的患者相对于整个肝部都有肿瘤的患者预后效果会更好。Anti-HCV(x4)为阳性,HbsAg 为阴性的患者会具有更好的预后效果。其次,数据说明肿瘤越大对预后影响也越大。

从图二可以看出,这里的变量的重要程度相差很大,再加上各变量之间可能存在相关性,为了让模型更加优化,我们考虑逐步回归方法重新进行建立统计模型。运行程序后有以下结果:
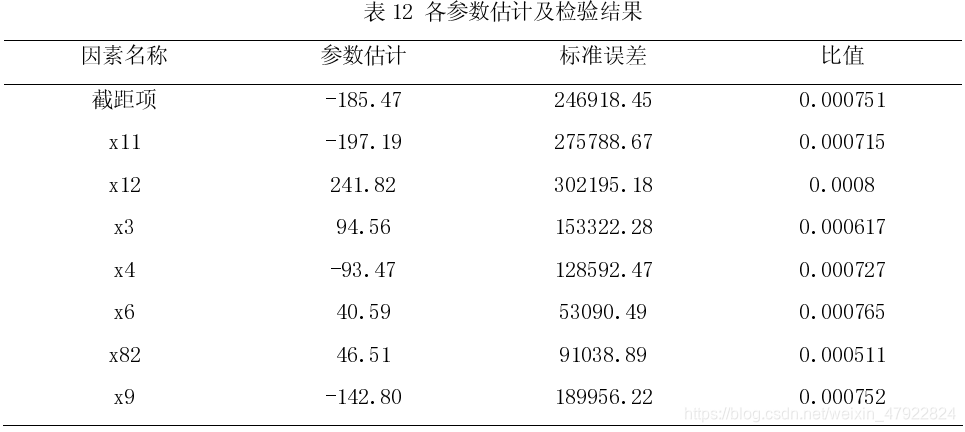
对比优化前的系数的比值(参数值/标准差),可见优化后的系数更有可能不为 0,从而优化的模型会相比优化前的模型更好。同时我们也可知:食道静脉曲张、HbsAg 和 Anti-HCV 的阴阳性、肿瘤大小、肿瘤的包膜否完整以及肿瘤旁的微小子灶等都对预后具有很大影响。
为此,我们得到两个模型如下,分别为全模型(没有优化的模型)和逐步回归简化模型
p ( Y ∗ = 1 ∣ X i ∗ ) ≈ p ( X i ∗ ′ β ^ ) = e X i ∗ ′ β ^ 1 + e X i ∗ ′ β ^ p(Y^* = 1|X_i^*)\approx p(X_i^{*'} \hat{\beta})=\frac{e^{X_i^{*'} \hat{\beta}}}{1+e^{X_i^{*'} \hat{\beta}}} p(Y∗=1∣Xi∗)≈p(Xi∗′β^)=1+eXi∗′β^eXi∗′β^
且 β ^ \hat{\beta} β^即为系数向量,其值分别由上述的表中的参数估计一列值给出,如对于优化的模型有:
X i ∗ ′ β ^ = 185.47197.19 x 11241.82 x 12 + 94.56 x 3 − 93.47 x 4 + 40.59 x 6 + 46.51 x 82 − 142.8 x 9 X_i^{*'} \hat{\beta}=185.47 197.19x11 241.82x12+94.56x3-93.47x4+40.59x6+46.51x82-142.8x9 Xi∗′β^=185.47197.19x11241.82x12+94.56x3−93.47x4+40.59x6+46.51x82−142.8x9
2.3.2 预测评估
实际工作中,逻辑回归的一个很重要应用就是预测。在这个案例中,我们能否利用已经建立的逻辑回归对预后影响进行预测?如果能,那么可以为患者根据自己的实际情况决定最佳的治疗方案。要达到此目的,必须具备两种能力:第一,具备预测能力;第二,具备对预测精度评估的能力。
由于只有 20 个观测,假如我们直接把这 20 个作为训练样本又作为测试样本,这既当运动员又当裁判的做法不符合我们严谨的态度,假如 8:2 来分开训练样本和测试样本,这也会导致原本就少的观测变得更少,而且测试样本也过少。为此,我们考虑留一法进行建模与预测,即每个观测都充 当一回测试样本,其余的进行建模,这样 20 次下来,我们得到两种模型对应的预测结果,即 p ( Y ∗ = 1 ∣ X i ∗ ) p(Y^* = 1|X_i^*) p(Y∗=1∣Xi∗),其中 yhat_all 为全模型的预测结果,yhat_step 为简化优化模型的结果,y 为最终 的判定值 1 为有影响,0 为无影响。

此概率 p ( Y ∗ = 1 ∣ X i ∗ ) p(Y^* = 1|X_i^*) p(Y∗=1∣Xi∗) i量化了肝癌患者治疗预后影响的可能性。显然,如果该可能性很大,我们更倾向于将 Y i ∗ Y_i^* Yi∗预测为 Y i ∗ = 1 Y_i^*=1 Yi∗=1;否则将 Y i ∗ Y_i^* Yi∗预测为 Y i ∗ = 0 Y_i^*=0 Yi∗=0, 但是到底多大的概率才叫大呢?为此,我们需要设置一个阈值α ,再定义一个预测规则如下:

如何选取阈值α 呢?显然,我们的目标是预测的准确。那么如何评判预测结果的准确性呢?不同的评判标准,量化手段会产生不同阈值α .
- 基于概率阈值α 的错判率(mis-classification rate,MCR)
M C R = 1 m I ( Y i ∗ ^ ≠ Y i ∗ ) MCR=\frac{1}{m}I(\hat{Y_i^*} \neq Y_i^*) MCR=m1I(Yi∗^=Yi∗)
其中m 为预测样本总数, I ( Y i ∗ ^ ≠ Y i ∗ ) I(\hat{Y_i^*} \neq Y_i^*) I(Yi∗^=Yi∗)为示性函数。
很明显, MCR 是错误判断的比率。如果 MCR =0,意味着所有的预测都正确; MCR =1,意味着所有预测都错误。我们的目标就是要极小化 MCR ,找到最优的阈值α .我们可以从 0 到 1 去搜索最优的阈值α ,使得 MCR 极小化即可,通过编程可得阈值范围(0,1)。
- 基于接受者曲线(ROC)模型效果评判
虽然我们可以按照上面所说的方法可以找到阈值α 最优解,但是我们这样考虑,如果建立的模型是这样的话,那么我们意味着把有影响划分到没有影响那类以及把没有影响划分到有影响那类是一样看待的。事实上,我们当然希望能够把对预后真实有影响的患者划分到有影响那一类,这样以尽早发现这类患者,才好做好各方面的医疗,降低预后的影响。而对于事实上没有影响的患者,我们也不希望把他划到有影响的一类,这样白白浪费医疗资源,而且会给患者带来沉重的经济负担。用数学语言来表达的话,即我们关注真实的 Y i ∗ = 0 Y_i^*=0 Yi∗=0预测为 Y ^ i ∗ = 1 \hat{Y}_i^*=1 Y^i∗=1的概率 p ( Y ^ i ∗ = 1 ∣ Y i ∗ = 0 ) p(\hat{Y}_i^* = 1|Y_i^*=0) p(Y^i∗=1∣Yi∗=0)以及真实的 Y i ∗ = 1 Y_i^*=1 Yi∗=1预测为 Y ^ i ∗ = 1 \hat{Y}_i^*=1 Y^i∗=1的概率 p ( Y ^ i ∗ = 1 ∣ Y i ∗ = 1 ) p(\hat{Y}_i^* = 1|Y_i^*=1) p(Y^i∗=1∣Yi∗=1)。我们自然希望TPR True positive rate)= p ( Y ^ i ∗ = 1 ∣ Y i ∗ = 1 ) p(\hat{Y}_i^* = 1|Y_i^*=1) p(Y^i∗=1∣Yi∗=1)的概率越大越好,而FPR False positive rate)= p ( Y ^ i ∗ = 1 ∣ Y i ∗ = 0 ) p(\hat{Y}_i^* = 1|Y_i^*=0) p(Y^i∗=1∣Yi∗=0)越小越好。对于任给的一个阈值α ,我们相应地可以算出 TPR 以及 FPR 的值,于是把(FPR,TPR)在坐标轴上展示出来,越靠近左上方的点其效果越好,此时 ROC 曲线下面积也就是越大说明分类效果越好。为此,我们画出优化模型留一法得出的 ROC 曲线图,如图三:
图中红色曲线是优化后模型采用留一法得到的 ROC 曲线,而蓝色曲线是没有优化的模型留一法画出的 ROC 曲线。其中红色 ROC 曲线下面积为 0.7802,而蓝色曲线下面积为 0.6538,从这两个数据来看并结合图表来看,用筛选后的这几个变量来建立逻辑回归的分类器,具有一定的准确性,效果还是比较明显的,有一定的可泛化性。而全模型 ROC 曲线下的面积说明分类器的准确性较差,说明优化模型相对更好。
到此为止,我们已经确定选择优化模型作为我们较好的预测模型,但阈值该选什么呢?在阈值的选择方面,我们按照(FPR,TPR)尽量往(0,1)靠近的原则,为此编程得到当阈值α 从 0.005到 0.995 变化时,留一法检验时,分类器都将 9 个有预后影响的预测为有影响的为 5 个预测为没有影响有四个,11 个没有影响的预测为有影响的有 2 个没有影响的有 9 个,总体的预测正确率为 70%,此时 MCR =30%, 我们在这里取阈值α 使得效果最好的取值的平均数,即取阈值α =0.5,这也符合我们的常识,即当预测为 1 类的概率大于 50%时,我们就将该患者预测为 1 类,否则预测为 0 类。

3. 结论
3.1. 模型结论
通过对结果的对比分析,我们最终得到如下的逻辑回归模型:
p ( Y ∗ = 1 ∣ X i ∗ ) ≈ p ( X i ∗ ′ β ^ ) = e X i ∗ ′ β ^ 1 + e X i ∗ ′ β ^ p(Y^* = 1|X_i^*)\approx p(X_i^{*'} \hat{\beta})=\frac{e^{X_i^{*'} \hat{\beta}}}{1+e^{X_i^{*'} \hat{\beta}}} p(Y∗=1∣Xi∗)≈p(Xi∗′β^)=1+eXi∗′β^eXi∗′β^
其中 X i ∗ ′ β ^ X_i^{*'} \hat{\beta} Xi∗′β^=-185.47 197.19x11 241.82x12+94.56x3-93.47x4+40.59x6+46.51x82-142.8x9。
且分类器,即预测的分类规则为

假如全部样本都拿来做训练样本并用原样本做检验,可得全部的样本都预测正确,即:
M C R = 1 m I ( Y i ∗ ^ ≠ Y i ∗ ) = 0 MCR=\frac{1}{m}I(\hat{Y_i^*} \neq Y_i^*)=0 MCR=m1I(Yi∗^=Yi∗)=0
该分类器交叉验证(留一检验)错判率为:
M C R = 1 m I ( Y i ∗ ^ ≠ Y i ∗ ) = 0.3 MCR=\frac{1}{m}I(\hat{Y_i^*} \neq Y_i^*)=0.3 MCR=m1I(Yi∗^=Yi∗)=0.3
其 ROC 曲线图如上图,ROC 曲线下面积为 0.7802 可见这个分类器效果还是比较准确的,具有比较优良的泛化性。
以上的结论表明,这模型的预测效果还是不错的。若希望进一步提高模型的应用,我们可以通过以逻辑回归判别模型为基模型,进行深入的 bagging 方法进行建模,产生更强的分类器,以帮助分析,得出更有建设性的结论。
3.2. 手术和治疗方案建议
通过逻辑回归法的建模分析,我们发现是否有食道静脉曲张、HbsAg 和 Anti-HCV 的阴阳性、肿瘤大小、肿瘤的包膜否完整以及肿瘤旁的微小子灶等都对预后具有很大的影响。因此,我们提出如下的手术和治疗方案建议:
-
HbsAg 和 Angi-HCV 分别为为乙肝表面抗原和丙肝表面抗原,如果阳性代表有乙肝病毒和丙肝病毒。而感染乙肝和丙肝病毒对肝细胞伤害大,需要重点进行抗病毒处理。如果已经出现肝癌, 需要进行手术,医生应注意手术期间的防护以免发生感染。
-
是否有肿瘤旁的微小子灶,肿瘤的包膜是否完整这三个指标都是判断癌细胞是否发生转移的指标,其中肿瘤旁的微小子灶是肝癌发生肝内转移的地方。如果癌细胞发生转移,那么治疗方案中需要在原来的基础上补充进行化疗。而且出现转移提示病情已经比较严重。
-
存在食道静脉曲张是肝硬化和肝癌的一个临床表现,表明干细胞功能减退,引起水钠滞留,同时也提示病人病情比较严重,随时有上消化道出血并发症的可能。因此在手术后可以做手术改善处理,可以采取 TIPS、分流和断流三种不同的方式。
4. 参考文献
[1]. Alan Julian Izenman . Modern Multivariate Statisitical Techniques,Philadelphia,Pennsylvabia,April 2008.
5. 附录
5.1 附录一
#描述统计 in R #
library(sqldf)
a=read.table("t3.txt",header=T)
a$y=(a$DECISION=="Y")
sqldf(" select X1,count(*), avg(y) from a group by X1 order by avg(y) ")
sqldf(" select X2, count(*),avg(y) from a group by X2 order by avg(y) ")
sqldf(" select X3, count(*),avg(y) from a group by X3 order by avg(y) ")
sqldf(" select X4,count(*), avg(y) from a group by X4 order by avg(y) ")
sqldf(" select X5, count(*),avg(y) from a group by X5 order by avg(y) ")
sqldf(" select X6,count(*), avg(y) from a group by X6 order by avg(y) ")
sqldf(" select X7, count(*),avg(y) from a group by X7 order by avg(y) ")
sqldf(" select X9, count(*),avg(y) from a group by X9 order by avg(y) ")
sqldf(" select X8, count(*),avg(y) from a group by X8 order by avg(y) ")
sqldf(" select X10,count(*), avg(y) from a group by X10 order by avg(y) ")
5.2 附录二
library(rpart)
library(MASS)
library(ROCR)
library(pROC)
library(sqldf)
#
a=read.table("t3.txt",header=T)
a$x11=1*(a$X1=='no')
a$x12=1*(a$X1=='light')
a$x13=1*(a$X1=='mid')
a$x21=1*(a$X2=='no')
a$x22=1*(a$X2=='branch')
a$x3=1*(a$X3=='positive')
a$x4=1*(a$X4=='positive')
a$x51=1*(a$X5=='leftliver')
a$x52=1*(a$X5=='rightliver')
a$x6=1.5*(a$X6=='small')+4*(a$X6=='middle')+7.5*(a$X6=='big')+10*(a$X6=='verybig')
a$x7=1*(a$X7=='dilation')
a$x81=1*(a$X8=='integrate')
a$x82=1*(a$X8=='part')
a$x9=1*(a$X9=='have')
a$x101=1*(a$X10=='no')
a$x102=1*(a$X10=='less')
a$y=1*(a$DECISION=='Y') dim(a)
data=a[,c(12:28)]
dim(data) #logistic regression for all valueables
mylogit <- glm(y~., data = data, family = binomial(logit))
summary(mylogit) mylogit1 <- step(glm(y~., data = data, family = binomial(logit)))
summary(mylogit1)
fmla <-paste(names(data)[17],"~", paste(names(data)[1: length(names(data[,1:17]))-1], collapse="+"))
fmla <- as.formula(fmla) #留一交叉检验
for(i in 1:20){
#split function to split dataset into training set and validate set
splitdf <- function(dataframe, i) { validateindex=i trainset <- dataframe[-validateindex, ] validateset <- dataframe[validateindex, ] list(trainset=trainset,validateset=validateset)
}
splitdata <- splitdf(data, i)
train_data <- splitdata$trainset
validate_data <- splitdata$validateset #logistic regression
mylogit <- glm(y~x11+x12+x3+x4+x6+x82+x9, data = train_data, family = binomial(logit)) predict_mylogit <- predict(mylogit, newdata = validate_data, type = "response")
if (i==1) {
predict_mylogit1=predict_mylogit }
if (i==2) {
predict_mylogit2=predict_mylogit }
if (i==3) {
predict_mylogit3=predict_mylogit }
if (i==4) {
predict_mylogit4=predict_mylogit }
if (i==5) {
predict_mylogit5=predict_mylogit }
if (i==6) {
predict_mylogit6=predict_mylogit }
if (i==7) {
predict_mylogit7=predict_mylogit }
if (i==8) {
predict_mylogit8=predict_mylogit }
if (i==9) {
predict_mylogit9=predict_mylogit }
if (i==10) {
predict_mylogit10=predict_mylogit }
if (i==11) {
predict_mylogit11=predict_mylogit }
if (i==12) {
predict_mylogit12=predict_mylogit }
if (i==13) {
predict_mylogit13=predict_mylogit }
if (i==14) {
predict_mylogit14=predict_mylogit }
if (i==15) {
predict_mylogit15=predict_mylogit }
if (i==16) {
predict_mylogit16=predict_mylogit }
if (i==17) {
predict_mylogit17=predict_mylogit }
if (i==18) {
predict_mylogit18=predict_mylogit }
if (i==19) {
predict_mylogit19=predict_mylogit }
if (i==20) {
predict_mylogit20=predict_mylogit }
} predict_mylogit0=c(predict_mylogit1,predict_mylogit2,predict_mylogit3,predict_mylogit4,predict_mylog
it5,predict_mylogit6,predict_mylogit7,predict_mylogit8,predict_mylogit9,predict_mylogit10,predict_my
logit11,predict_mylogit12,predict_mylogit13,predict_mylogit14,predict_mylogit15,predict_mylogit16,pr
edict_mylogit17,predict_mylogit18,predict_mylogit19,predict_mylogit20) for(i in 1:20){
#split function to split dataset into training set and validate set
splitdf <- function(dataframe, i) { validateindex=i trainset <- dataframe[-validateindex, ] validateset <- dataframe[validateindex, ] list(trainset=trainset,validateset=validateset)
}
splitdata <- splitdf(data, i)
train_data <- splitdata$trainset
validate_data <- splitdata$validateset #logistic regression
mylogit <- glm(fmla, data = train_data, family = binomial(logit))
predict_mylogit <- predict(mylogit, newdata = validate_data, type = "response")
if (i==1) {
predict_mylogit1=predict_mylogit }
if (i==2) {
predict_mylogit2=predict_mylogit }
if (i==3) {
predict_mylogit3=predict_mylogit }
if (i==4) {
predict_mylogit4=predict_mylogit }
if (i==5) {
predict_mylogit5=predict_mylogit }
if (i==6) {
predict_mylogit6=predict_mylogit }
if (i==7) {
predict_mylogit7=predict_mylogit }
if (i==8) {
predict_mylogit8=predict_mylogit }
if (i==9) {
predict_mylogit9=predict_mylogit }
if (i==10) {
predict_mylogit10=predict_mylogit }
if (i==11) {
predict_mylogit11=predict_mylogit }
if (i==12) {
predict_mylogit12=predict_mylogit }
if (i==13) {
predict_mylogit13=predict_mylogit }
if (i==14) {
predict_mylogit14=predict_mylogit }
if (i==15) {
predict_mylogit15=predict_mylogit }
if (i==16) {
predict_mylogit16=predict_mylogit }
if (i==17) {
predict_mylogit17=predict_mylogit }
if (i==18) {
predict_mylogit18=predict_mylogit }if (i==19) {
predict_mylogit19=predict_mylogit }
if (i==20) {
predict_mylogit20=predict_mylogit }
}
predict_mylogit1=c(predict_mylogit1,predict_mylogit2,predict_mylogit3,predict_mylogit4,predict_mylog
it5,predict_mylogit6,predict_mylogit7,predict_mylogit8,predict_mylogit9,predict_mylogit10,predict_my
logit11,predict_mylogit12,predict_mylogit13,predict_mylogit14,predict_mylogit15,predict_mylogit16,pr
edict_mylogit17,predict_mylogit18,predict_mylogit19,predict_mylogit20) cbind(predict_mylogit1,predict_mylogit0) #ROC
#ROC
pred<- prediction(predict_mylogit0,data[,17])
perf<- performance(pred, "tpr","fpr" )
pred1<- prediction(predict_mylogit1,data[,17])
perf1<- performance(pred1, "tpr","fpr" )
plot(perf)
plot(perf, main="Logistic Regression OC Curve",xlab="False positive rate", ylab="True positive
rate",col="red")
plot(perf1,col="blue",add=T)
roc(data[,12], predict_mylogit0)
roc(data[,12], predict_mylogit1)for(i in 1:20){
print(i*0.05)
print(table((predict_mylogit0>0.05*i)*1,data$y))
}
这篇关于“泰迪杯”挑战赛 - 通过数据挖掘预测肝癌手术治疗效果的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








