2018-2019 ACM-ICPC, Asia Jiaozuo Regional Contest D.Keiichi Tsuchiya the Drift King（几何）

本文主要是介绍2018-2019 ACM-ICPC, Asia Jiaozuo Regional Contest D.Keiichi Tsuchiya the Drift King（几何），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接：https://codeforc.es/gym/102028/problem/D

Drifting is a driving style in which the driver uses the throttle, brakes, clutch, gear shifting and steering input to keep the car in a state of oversteer while manoeuvring from turn to turn. As a sport, the drifting was first practised in Japan in the late 80s before gaining worldwide popularity in the decade that followed.

Keiichi Tsuchiya is a Japanese driver who is better known as the Drift King. He played an important role in popularizing the art of drifting. This pioneer inspired many successful drivers. He appeared in the movie The Fast and the Furious: Tokyo Drift and he is often employed on various movie sets as both driver and stunt coordinator. Keiichi Tsuchiya’s talent in the drifting is especially true of his big stunt, the ultimate drifting.

Here is what he could do. The drift car he drives is shaped like a rectangular box of width a inches and of length b inches. He makes a right turn of a curve whose internal boundary is an arc with d degrees in a circle with a radius of r inches. As a super-skilled driver, he maintains his car to keep the contact and tangency at the internal boundary. That is, the right front corner of the car should always run along the internal boundary and the direction of the car body should always be tangential to the internal boundary.
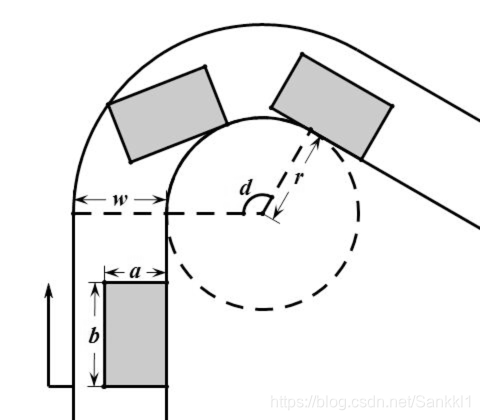
在这里插入图片描述

We have measured that the straightaways before and after the curve are long enough, and the width of the lane is invariable. As what we meet in real life, if a lane has a fixed width, for each point of its one side, the distance to the nearest point of the other side is exactly its width. Now you are asked to calculate the minimal width w of the lane so that the Drift King could drive throughout the curve without drifting out of the lane.

Input
The input contains several test cases, and the first line contains a positive integer T indicating the number of test cases which is up to 104.

For each test case, the only one line contains four integers a, b, r and d, where 0<a,b,r<100 and 0<d<180.

Output
For each test case, output a line containing the minimal width (in inches) of the lane with an absolute or relative error of at most 10−6. Precisely speaking, assuming that your answer is a and the jury’s answer is b, your answer will be considered correct if |a−b|max{1,|b|}≤10−6.

Example

input

output

1.605551275464
1.605551275464
1.598076211353
1.415415569072

题意

漂移王要顺利飘逸过弯，车的一边始终与弯道相切，在过程中车身不能再路面以外，求路宽度最小是多少。

分析

一道几何体，我们设车的左下角为 X ，圆心 O 与 X 相连，发现如果 OX 在弯道的圆弧范围内，那么最窄至少要 sqrt((a + r) * (a + r) + b * b) - r （可以直接用勾股定律算出）；如果在圆弧范围外的话，我们可以用相似三角形推出最小宽度。

代码

#include<bits/stdc++.h>
using namespace std;int t;
double a,b,r,d;int main()
{//printf("%.10lf",tan(3.1415 / 6.0));scanf("%d",&t);while(t--){scanf("%lf%lf%lf%lf",&a,&b,&r,&d);double D = d;d = d / 180.0 * 3.1415926;double temp = sqrt((a + r) * (a + r) + b * b) - r;double ans = temp;if(D < 90 && tan(d) < b / (a + r)){double x1 = tan(d) * (a + r);double y2 = b - x1;double y1 = sqrt((a + r) * (a + r) + x1 * x1);double x2 = y2 * sin(d);double temp2 = y1 + x2 - r;if(temp2 > 0) ans = min(ans, temp2);}printf("%.12lf\n",ans);}return 0;
}