本文主要是介绍机器学习——SVM的回归形式(SVR),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
岭回归(ridge regression)
在前面的一篇博客(机器学习——线性回归(Linear Regression))中提到,线性回归的解析解如下,
w = ( X T X ) − 1 X T y w = {({X^T}X)^{ - 1}}{X^T}y w=(XTX)−1XTy
其中,X的维数为 N × ( d + 1 ) N \times (d + 1) N×(d+1)。因为大多数情况下样本量(N)是远大于特征数(d)的,所以, X T X X^TX XTX常常是可逆的。但当X不是列满秩矩阵时,即特征数比样本数还要多,则 X T X X^TX XTX的行列式为0, X T X X^TX XTX不可逆;或者X的某些列的线性相关性比较大时, X T X X^TX XTX的行列式接近0,此时 X T X X^TX XTX为病态矩阵,此时计算逆矩阵误差会比较大。
为了解决 X T X X^TX XTX矩阵求逆的问题,给矩阵 X T X X^TX XTX加上一个 λ I \lambda I λI,从而使矩阵非奇异,进而能对 X T X + λ I {X^T}X + \lambda I XTX+λI求逆,这就是岭回归。
即岭回归的系数计算式为,
W = ( X T X + λ I ) − 1 X T Y W = {({X^T}X + \lambda I)^{ - 1}}{X^T}Y W=(XTX+λI)−1XTY
上式中的 λ I \lambda I λI其实是正则化的一种体现,上式是L2-regularized linear regression的解析解,计算过程描述如下:
首先,L2-regularized linear regression的问题可以描述为,
min w    λ N w T w + 1 N ∑ n = 1 N ( y n − w T x n ) 2 \mathop {\min }\limits_w \;\frac{\lambda }{N}{w^T}w + \frac{1}{N}\sum\limits_{n = 1}^N {{{({y_n} - {w^T}{x_n})}^2}} wminNλwTw+N1n=1∑N(yn−wTxn)2
写成矩阵形式为,
min w    λ N w T w + 1 N ∥ X w − y ∥ 2 \mathop {\min }\limits_w \;\frac{\lambda }{N}{w^T}w + \frac{1}{N}{\left\| {Xw - y} \right\|^2} wminNλwTw+N1∥Xw−y∥2
对上式求梯度,
∇ ( w ) = 2 λ N w + 1 N ( 2 X T X w − 2 X T y ) = 2 N ( ( λ I + X T X ) w − X T y ) = 0 \nabla (w) = \frac{{2\lambda }}{N}w + \frac{1}{N}(2{X^T}Xw - 2{X^T}y) = \frac{2}{N}((\lambda I + {X^T}X)w - {X^T}y) = 0 ∇(w)=N2λw+N1(2XTXw−2XTy)=N2((λI+XTX)w−XTy)=0
令梯度为0,求得系数w,为,
w = ( X T X + λ I ) − 1 X T Y w = {({X^T}X + \lambda I)^{ - 1}}{X^T}Y w=(XTX+λI)−1XTY
所以,岭回归的系数解析解其实是对线性回归进行L2正则化的一种体现。
最小二乘支持向量机(LSSVM)
在上一篇博客中,提到了Representer Theorem,即对于任意的L2正则化的线性模型,其最佳化的 w w w均可表示为资料线性组合的形式,所以可以考虑把Kernel用在岭回归里,叫做kernel ridge regression。
由于 w = ∑ i = 0 N β n z n w = \sum\limits_{i = 0}^N {{\beta _n}{z_n}} w=i=0∑Nβnzn,所以一旦把岭回归kernel化之后,实际上就是用参数 β \beta β取代了原来的参数 w w w,则现在的kernel ridge regression问题可以描述如下,
min β    λ N ∑ n = 1 N ∑ m = 1 N β n β m K ( x n , x m ) + 1 N ∑ n = 1 N ( y n − ∑ m = 1 N β m K ( x n , x m ) ) 2      = λ N β T K β + 1 N ( ∥ y − K β ∥ 2 )                − 转 化 为 矩 阵 形 式      = λ N β T K β + 1 N ( β T K T K β − 2 β T K T y + y T y ) \begin{array}{l} \mathop {\min }\limits_\beta \;\frac{\lambda }{N}\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {{\beta _n}{\beta _m}K({x_n},{x_m})} + \frac{1}{N}} \sum\limits_{n = 1}^N {{{({y_n} - \sum\limits_{m = 1}^N {{\beta _m}K({x_n},{x_m})} )}^2}} \\\\ \;\; = \frac{\lambda }{N}{\beta ^T}K\beta + \frac{1}{N}({\left\| {y - K\beta } \right\|^2})\;\;\;\;\;\;\;-转化为矩阵形式\\\\ \;\; = \frac{\lambda }{N}{\beta ^T}K\beta + \frac{1}{N}({\beta ^T}{K^T}K\beta - 2{\beta ^T}{K^T}y + {y^T}y) \end{array} βminNλn=1∑Nm=1∑NβnβmK(xn,xm)+N1n=1∑N(yn−m=1∑NβmK(xn,xm))2=NλβTKβ+N1(∥y−Kβ∥2)−转化为矩阵形式=NλβTKβ+N1(βTKTKβ−2βTKTy+yTy)
求上式的梯度,如下,
∇ E ( β ) = 2 N ( λ K T I β + K T K β − K T y )                          = 2 N K T ( ( λ I + K ) β − y ) ( 这 里 的 K 是 一 个 半 正 定 的 对 称 矩 阵 ) \begin{array}{l} \nabla E(\beta ) = \frac{2}{N}(\lambda {K^T}I\beta + {K^T}K\beta - {K^T}y)\\\\ \;\;\;\;\;\;\;\;\;\;\;\; = \frac{2}{N}{K^T}((\lambda I + K)\beta - y)\\\\ (这里的K是一个半正定的对称矩阵) \end{array} ∇E(β)=N2(λKTIβ+KTKβ−KTy)=N2KT((λI+K)β−y)(这里的K是一个半正定的对称矩阵)
让 ∇ E ( β ) = 0 \nabla {\rm{E}}(\beta ) = 0 ∇E(β)=0,可以得到如下的解析解,
β = ( λ I + K ) − 1 y \beta = {(\lambda I + K)^{ - 1}}y β=(λI+K)−1y
该解一定存在,因为 λ > 0 \lambda > 0 λ>0,并且K一定是一个半正定矩阵,所以, λ I + K \lambda I + K λI+K一定可逆。
上面的是kernel ridge regression的参数求解过程,而LSSVM实际上就是kernel ridge regression用于分类的情况,即,
但LSSVM求解的时间复杂度达到了 O ( N 3 ) O(N^3) O(N3),且求解过程中,矩阵K是稠密的。
下面是linear ridge regression和kernel ridge regression的一个对比,
| linear ridge regression | kernel ridge regression |
|---|---|
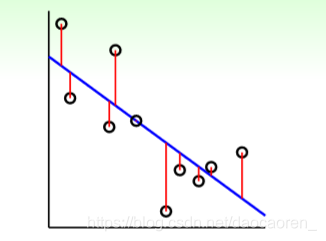 | 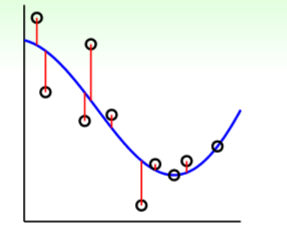 |
| w = ( X T X + λ I ) − 1 X T Y w = {({X^T}X + \lambda I)^{ - 1}}{X^T}Y w=(XTX+λI)−1XTY | β = ( λ I + K ) − 1 y \beta = {(\lambda I + K)^{ - 1}}y β=(λI+K)−1y |
| 限制更多,形状比较简单 | 更加灵活,边界可以很复杂 |
| 训练复杂度: O ( d 3 + d 2 N ) O(d^3+d^2N) O(d3+d2N) 预测复杂度: O ( d ) O(d) O(d) | 训练复杂度: O ( N 3 ) O(N^3) O(N3) 预测复杂度: O ( N ) O(N) O(N) |
| 当 N > > d N>>d N>>d时,计算很高效 | 对于样本数多的情况,计算量太大 |
所以,从上表可以看出,linear与kernel其实就是对efficiency和flexibility的一个取舍。
Tube Regression
在介绍Tube Regression之前,首先先对Soft-Margin SVM和LSSVM做一个对比,下面两张图是对同一个案例,分别用这两方法所求得的边界示意,

图中,正方形所框选出的都是支持向量(SVs),从中可以看出,LSSVM有更多的SVs,这就意味着其参数 β \beta β是稠密的,预测起来,也会更慢。但之前说过 ,标准的SVM求得的系数 α \alpha α是稀疏的,所以,要找到一种方法,获得一个稀疏的 β \beta β——Tube Regression。
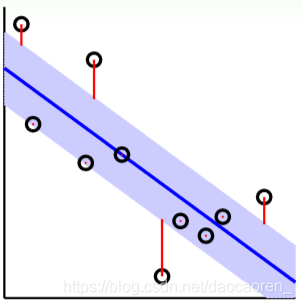
- 在tube内(紫色区域内):没有错误
- 在tube外:计算到tube的距离当作error(红色线为error)
则其误差衡量方式为,
e r r ( y , s ) = max ( 0 , ∣ s − y ∣ − ε ) err(y,s) = \max (0,\left| {s - y} \right| - \varepsilon ) err(y,s)=max(0,∣s−y∣−ε)
这中误差叫做 ε − i n s e n s i t i v e      e r r o r {\rm{\varepsilon - insensitive\;\; error}} ε−insensitiveerror,有如下关系,
当 ∣ s − y ∣ ≤ ε : 误 差 为 0 当 ∣ s − y ∣ > ε : 误 差 为 ∣ s − y ∣ − ε \begin{array}{l} 当\left| {s - y} \right| \le \varepsilon :误差为0\\ 当\left| {s - y} \right| > \varepsilon :误差为\left| {s - y} \right|{\rm{ - }}\varepsilon \end{array} 当∣s−y∣≤ε:误差为0当∣s−y∣>ε:误差为∣s−y∣−ε
下面将Tube Regression和Squared Regression做一个对比,
| Tube Regression | Squared Regression |
|---|---|
 |  |
误差图像如下,
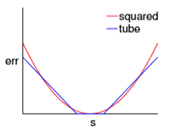
- 当 ∣ s − y ∣ \left| {s - y} \right| ∣s−y∣很小时, t u b e ≈ s q u a r e d tube \approx squared tube≈squared;
- 当 ∣ s − y ∣ \left| {s - y} \right| ∣s−y∣越来越小时,即从中间向两边,tube增长缓慢,不容易受noise影响。
加入L2 regularizer之后,即L2-Regularized Tube Regression描述如下,
min w    λ N w T w + 1 N ∑ n = 1 N max ( 0 , ∣ w T z n − y ∣ − ε ) \mathop {\min }\limits_w \;\frac{\lambda }{N}{w^T}w + \frac{1}{N}\sum\limits_{n = 1}^N {\max (0,\left| {{w^T}{z_n} - y} \right| - \varepsilon )} wminNλwTw+N1n=1∑Nmax(0,∣∣wTzn−y∣∣−ε)
将上式改写,可得到SVR的原始形式如下,
min b , w    1 2 w T w + C ∑ n = 1 N max ( 0 , ∣ w T z n + b − y n ∣ − ε )                                  — — S t a n d a r d      S V R      P r i m a l \mathop {\min }\limits_{b,w} \;\frac{1}{2}{w^T}w + C\sum\limits_{n = 1}^N {\max (0,\left| {{w^T}{z_n} + b - {y_n}} \right| - \varepsilon )}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;——Standard \;\;SVR \;\;Primal b,wmin21wTw+Cn=1∑Nmax(0,∣∣wTzn+b−yn∣∣−ε)——StandardSVRPrimal
上述问题的形式,比方便求解,对比之前SVM部分的推导,将其进行改写,改写后的等价最优化问题如下,
min b , w , ξ ∧ , ξ ∨      1 2 w T w + C ∑ n = 1 N ( ξ n ∨ + ξ n ∧ )        s . t .        − ε − ξ n ∨ ≤ y n − w T z n − b ≤ ε + ξ n ∧                              ξ n ∨ ≥ 0 , ξ n ∧ ≥ 0 \begin{array}{l} \mathop {\min }\limits_{b,w,{\xi ^ \wedge },{\xi ^ \vee }} \;\;\frac{1}{2}{w^T}w + C\sum\limits_{n = 1}^N {(\xi _n^ \vee + \xi _n^ \wedge )} \\\\ \;\;\;s.t.\;\;\; - \varepsilon - \xi _n^ \vee \le {y_n} - {w^T}{z_n} - b \le \varepsilon + \xi _n^ \wedge \\\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\xi _n^ \vee \ge 0,\xi _n^ \wedge \ge 0 \end{array} b,w,ξ∧,ξ∨min21wTw+Cn=1∑N(ξn∨+ξn∧)s.t.−ε−ξn∨≤yn−wTzn−b≤ε+ξn∧ξn∨≥0,ξn∧≥0
其中,参数C的含义:regularization和tube violation的权衡
参数 ε \varepsilon ε的含义:tube的宽度
上述问题可用QP来求解,共有 d ~ + 1 + 2 N \tilde d + 1 + 2N d~+1+2N个变量,4N条约束,接下来,就是把primal问题转为dual问题,移除对 d ~ \tilde d d~的依赖。
引入拉格朗日乘子 α ∧ & α ∨ {\alpha ^ \wedge }\& {\alpha ^ \vee } α∧&α∨:
目 标 方 程                    1 2 w T w + C ∑ n = 1 N ( ξ n ∨ + ξ n ∧ ) 加 入 α n ∧          f o r            y n − w T z n − b ≤ ε + ξ n ∧ 加 入 α n ∨          f o r      − ε − ξ n ∨ ≤ y n − w T z n − b \begin{array}{l} 目标方程\;\;\;\;\;\;\;\;\;\frac{{\rm{1}}}{{\rm{2}}}{w^T}w + C\sum\limits_{n = 1}^N {(\xi _n^ \vee + \xi _n^ \wedge )} \\\\ 加入\alpha _n^ \wedge \;\;\;\;for\;\;\;\;\;{y_n} - {w^T}{z_n} - b \le \varepsilon + \xi _n^ \wedge \\\\ 加入\alpha _n^ \vee \;\;\;\;for\;\; - \varepsilon - \xi _n^ \vee \le {y_n} - {w^T}{z_n} - b \end{array} 目标方程21wTw+Cn=1∑N(ξn∨+ξn∧)加入αn∧foryn−wTzn−b≤ε+ξn∧加入αn∨for−ε−ξn∨≤yn−wTzn−b
KKT条件:
∂ L ∂ w i = 0 :                w = ∑ n = 1 N ( α n ∧ − α n ∨ ⎵ β n ) z n ∂ L ∂ b = 0 :                  ∑ n = 1 N ( α n ∧ − α n ∨ ) = 0 c o m p l e m e n t a r y      s l a c k n e s s : α n ∧ ( ε + ξ n ∧ − y n + w T z n + b ) = 0 α n ∨ ( ε + ξ n ∨ + y n − w T z n − b ) = 0 \begin{array}{l} \frac{{\partial L}}{{\partial {w_i}}} = 0:\;\;\;\;\;\;\;w = \sum\limits_{n = 1}^N {(\underbrace {\alpha _n^ \wedge - \alpha _n^ \vee }_{{\beta _n}})} {z_n}\\\\ \frac{{\partial L}}{{\partial b}} = 0:\;\;\;\;\;\;\;\;\sum\limits_{n = 1}^N {(\alpha _n^ \wedge - \alpha _n^ \vee )} = 0\\\\ {\rm{complementary \;\;slackness:}}\begin{array}{} {\alpha _n^ \wedge (\varepsilon + \xi _n^ \wedge - {y_n} + {w^T}{z_n} + b) = 0}\\ {\alpha _n^ \vee (\varepsilon + \xi _n^ \vee + {y_n} - {w^T}{z_n} - b) = 0} \end{array} \end{array} ∂wi∂L=0:w=n=1∑N(βn αn∧−αn∨)zn∂b∂L=0:n=1∑N(αn∧−αn∨)=0complementaryslackness:αn∧(ε+ξn∧−yn+wTzn+b)=0αn∨(ε+ξn∨+yn−wTzn−b)=0
推导过程略,下面直接给出SVR Dual:
min    1 2 ∑ n = 1 N ∑ m = 1 N ( α n ∧ − α n ∨ ) ( α m ∧ − α m ∨ ) K n , m + ∑ n = 1 N ( ( ε − y n ) ⋅ α n ∧ + ( ε + y n ) ⋅ α n ∨ ) s . t .    ∑ n = 1 N ( α n ∧ − α n ∨ )              0 ≤ α n ∧ ≤ C , 0 ≤ α n ∨ ≤ C \begin{array}{l} \min \;\frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{m = 1}^N {(\alpha _n^ \wedge - \alpha _n^ \vee )(\alpha _m^ \wedge - \alpha _m^ \vee ){K_{n,m}}} } + \sum\limits_{n = 1}^N {((\varepsilon - {y_n}) \cdot \alpha _n^ \wedge + (\varepsilon + {y_n}) \cdot \alpha _n^ \vee )} \\\\ s.t.\;\sum\limits_{n = 1}^N {(\alpha _n^ \wedge - \alpha _n^ \vee )} \\\\ \;\;\;\;\;\;0 \le \alpha _n^ \wedge \le C,0 \le \alpha _n^ \vee \le C \end{array} min21n=1∑Nm=1∑N(αn∧−αn∨)(αm∧−αm∨)Kn,m+n=1∑N((ε−yn)⋅αn∧+(ε+yn)⋅αn∨)s.t.n=1∑N(αn∧−αn∨)0≤αn∧≤C,0≤αn∨≤C
与QP的形式相似,可以用相似的求解器来求解。
SVR解的稀疏性解释:
根据KKT条件,有如下关系:
w = ∑ n = 1 N ( α n ∧ − α n ∨ ⎵ β n ) z n c o m p l e m e n t a r y      s l a c k n e s s : α n ∧ ( ε + ξ n ∧ − y n + w T z n + b ) = 0 α n ∨ ( ε + ξ n ∨ + y n − w T z n − b ) = 0 \begin{array}{l} w = \sum\limits_{n = 1}^N {(\underbrace {\alpha _n^ \wedge - \alpha _n^ \vee }_{{\beta _n}})} {z_n}\\ {\rm{complementary\;\; slackness:}}\begin{array}{} {\alpha _n^ \wedge (\varepsilon + \xi _n^ \wedge - {y_n} + {w^T}{z_n} + b) = 0}\\ {\alpha _n^ \vee (\varepsilon + \xi _n^ \vee + {y_n} - {w^T}{z_n} - b) = 0} \end{array} \end{array} w=n=1∑N(βn αn∧−αn∨)zncomplementaryslackness:αn∧(ε+ξn∧−yn+wTzn+b)=0αn∨(ε+ξn∨+yn−wTzn−b)=0
而根据tube regression,把数据点分为两部分,即
- 在tube之内的点,有,
∣ w T z n + b − y n ∣ < ε ⇒ ξ n ∧ = 0 , ξ n ∨ = 0 ⇒ ( ε + ξ n ∧ − y n + w T z n + b ) ≠ 0 , ( ε + ξ n ∨ + y n − w T z n − b ) ≠ 0 ⇒ α n ∧ = 0 , α n ∨ = 0 ⇒ β n = 0 \begin{array}{l} \left| {{w^T}{z_n} + b - {y_n}} \right| < \varepsilon \\\\ \Rightarrow \xi _n^ \wedge = 0,\xi _n^ \vee = 0\\\\ \Rightarrow (\varepsilon + \xi _n^ \wedge - {y_n} + {w^T}{z_n} + b) \ne 0,(\varepsilon + \xi _n^ \vee + {y_n} - {w^T}{z_n} - b) \ne 0\\\\ \Rightarrow \alpha _n^ \wedge = 0,\alpha _n^ \vee = 0\\\\ \Rightarrow {\beta _n} = 0 \end{array} ∣∣wTzn+b−yn∣∣<ε⇒ξn∧=0,ξn∨=0⇒(ε+ξn∧−yn+wTzn+b)̸=0,(ε+ξn∨+yn−wTzn−b)̸=0⇒αn∧=0,αn∨=0⇒βn=0
- 在tube之外的点,即SVs,则 β n ≠ 0 {\beta _n} \ne 0 βn̸=0
所以,SVR可以有一个稀疏解 β \beta β。
这篇关于机器学习——SVM的回归形式(SVR)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








