本文主要是介绍【启发式算法】白鲸优化算法【附python实现代码】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
写在前面:
首先感谢兄弟们的订阅,让我有创作的动力,在创作过程我会尽最大能力,保证作品的质量,如果有问题,可以私信我,让我们携手共进,共创辉煌。
路虽远,行则将至;事虽难,做则必成。只要有愚公移山的志气、滴水穿石的毅力,脚踏实地,埋头苦干,积跬步以至千里,就一定能够把宏伟目标变为美好现实。

1.介绍
白鲸优化算法(Beluga whale optimization, BWO)是2022年提出的一种元启发式优化算法,其灵感来源于白鲸的生活行为。白鲸以成年鲸的纯白色而闻名,是高度群居的动物,它们可以成群聚集,有2到25个成员,平均有10个成员。与其他元启发式方法类似,BWO包含探索阶段和开发阶段,此外该算法还模拟了生物界中存在的鲸落现象。
论文:
Zhong C, Li G, Meng Z. Beluga whale optimization: A novel nature-inspired metaheuristic algorithm[J]. Knowledge-Based Systems, 2022, 109215.

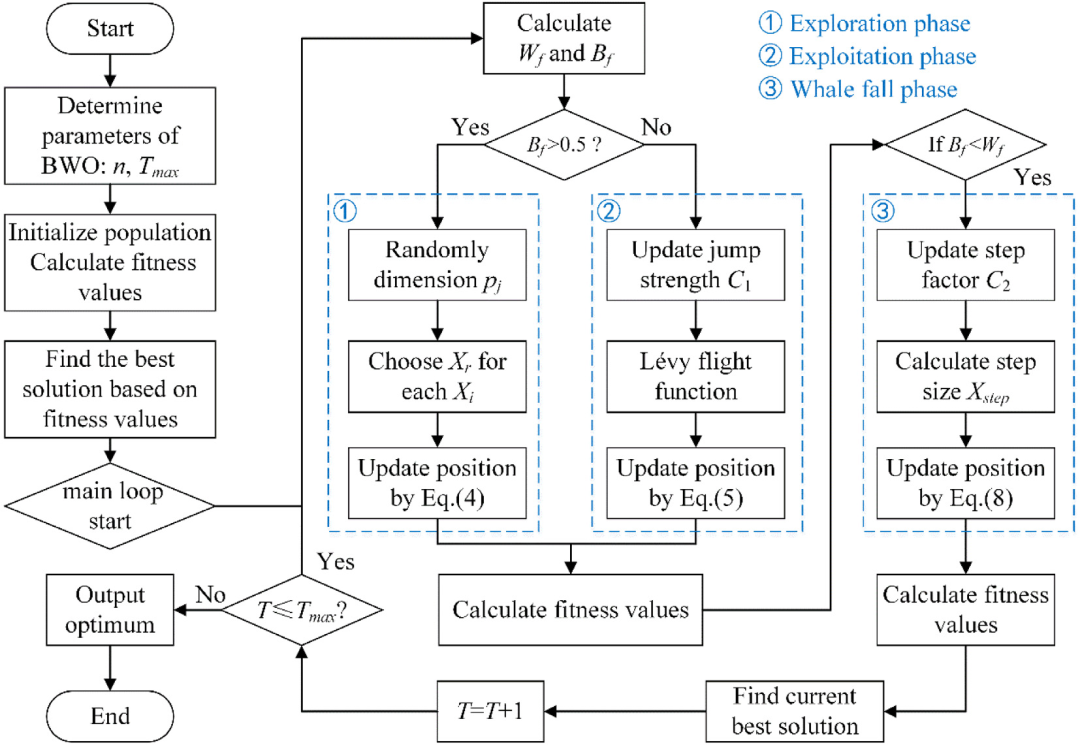
2.算法流程
BWO流程图:
2.1 种群初始化
白鲸优化算法是基于种群的机制,将每条白鲸假设为一个候选解,并在优化过程中进行不断更新,则种群初始化位置为:

2.2 探索阶段

2.3 开发阶段
开发阶段的灵感来自于白鲸的捕食行为,白鲸可以根据附近白鲸合作觅食和位置移动。假设可以通过 Levy 飞行策略捕捉猎物,其公式为:

2.4 鲸鱼坠落
为了模拟每次迭代中鲸鱼坠落行为,从种群中选择一个鲸鱼坠落的概率,来模拟群体中的变化。白鲸要么转移到其它地方,要么被击落并掉入深海。为保证种群数量不变,通过利用白鲸位置和鲸鱼坠落步长更新鲸鱼位置,公式如下:

式中,鲸鱼坠落的概率从初始迭代的 0.1 下降到最后一次迭代的 0.05 ,说明当白鲸在优化过程中更接近食物源时,白鲸的就会危险降低。
3.代码
BWO代码:
import numpy as np
import math
from copy import deepcopy
import matplotlib.pyplot as plt'''
白鲸优化算法
参数
n:白鲸种群大小
tmax:最大迭代次数
lb:变量下限
ub:变量上限
nd:变量维数
fobj:目标函数
'''# 白鲸优化算法
def bwo(n, tmax, lb, ub, nd, fobj):# 记录每轮更新最优解best_fval = []# 位置矩阵x = lb + np.random.random((n, nd)) * (ub - lb)# 适应值矩阵fobj_list = [fobj(x[i, ...]) for i in range(n)]fx = [f() for f in fobj_list]# 适应值拷贝矩阵temp_fx = deepcopy(fx)# 最优解和最优解值xposbest = x[np.argmin(fx)]fvalbest = min(fx)best_fval.append(fvalbest)# 循环更新for t in range(1, tmax + 1):# 位置拷贝矩阵temp_x = deepcopy(x)# 鲸落概率wf = 0.1 - 0.05 * (t / tmax)# 计算每只白鲸的平衡因子bfb0 = np.random.random(n)for b0_index in range(len(b0)):while b0[b0_index] == 0:b0[b0_index] = np.random.random()bf = b0 * (1 - t / (2 * tmax))# 更新每一只白鲸位置for i in range(n):# 探索阶段if bf[i] > 0.5:r1 = np.random.random()r2 = np.random.random()while r1 == 0:r1 = np.random.random()while r2 == 0:r2 = np.random.random()# 选择随机白鲸r = np.random.randint(0, n)while r == i:r = np.random.randint(0, n)pj = np.arange(nd)np.random.shuffle(pj)if nd <= n / 5:temp_x[i, pj[0]] = x[i, pj[0]] + (x[r, pj[0]] - x[i, pj[0]]) * (1 + r1) * np.sin(2 * np.pi * r2)temp_x[i, pj[1]] = x[i, pj[1]] + (x[r, pj[1]] - x[i, pj[1]]) * (1 + r1) * np.cos(2 * np.pi * r2)else:for j in range(int(nd / 2)):temp_x[i, 2 * j] = x[i, 2 * j] + (x[r, pj[1]] - x[i, 2 * j]) * (1 + r1) * np.sin(2 * np.pi * r2)temp_x[i, 2 * j + 1] = x[i, 2 * j + 1] + (x[r, pj[1]] - x[i, 2 * j + 1]) * (1 + r1) * np.cos(2 * np.pi * r2)# 开发阶段else:r3 = np.random.random()r4 = np.random.random()while r3 == 0:r3 = np.random.random()while r4 == 0:r4 = np.random.random()c1 = 2 * r4 * (1 - (t / tmax))# 随机白鲸r = np.random.randint(0, n)while r == i:r = np.random.randint(0, n)beta = 3 / 2delta = ((math.gamma(1 + beta) * np.sin((np.pi * beta) / 2))/ (math.gamma((1 + beta) / 2) * beta * (2 ** ((beta - 1) / 2)))) ** (1 / beta)u = np.random.randn(nd)v = np.random.randn(nd)lf = 0.05 * ((u * delta) / (abs(v) ** (1 / beta)))temp_x[i, ...] = r3 * xposbest - r4 * x[i, ...] + c1 * lf * (x[r, ...] - x[i, ...])# 处理超出边界值flaglb = np.asarray(temp_x[i, ...] < lb).astype(np.int8)flagub = np.asarray(temp_x[i, ...] > ub).astype(np.int8)flag = flaglb + flagubfor k in range(nd):if flag[k] == 0:flag[k] = 1else:flag[k] = 0temp_x[i, ...] = temp_x[i, ...] * flag + ub * flagub + lb * flaglbresult = fobj(temp_x[i, ...])temp_fx[i] = result()if temp_fx[i] < fx[i]:x[i, ...] = temp_x[i, ...]fx[i] = temp_fx[i]# 鲸落for i in range(n):if bf[i] <= wf:r5 = np.random.random()r6 = np.random.random()r7 = np.random.random()while r5 == 0:r5 = np.random.random()while r6 == 0:r6 = np.random.random()while r7 == 0:r7 = np.random.random()c2 = 2 * wf * n# 随机白鲸r = np.random.randint(0, n)xstep = (ub - lb) * (np.exp((-c2 * t) / tmax))temp_x[i, ...] = r5 * x[i, ...] - r6 * x[r, ...] + r7 * xstep# 处理超出边界值flaglb = np.asarray(temp_x[i, ...] < lb).astype(np.int8)flagub = np.asarray(temp_x[i, ...] > ub).astype(np.int8)flag = flaglb + flagubfor m in range(nd):if flag[m] == 0:flag[m] = 1else:flag[m] = 0temp_x[i, ...] = temp_x[i, ...] * flag + ub * flagub + lb * flaglbresult = fobj(temp_x[i, ...])temp_fx[i] = result()if temp_fx[i] < fx[i]:x[i, ...] = temp_x[i, ...]fx[i] = temp_fx[i]# 更改最优值temp_xposbest = x[np.argmin(fx)]temp_fvalbest = min(fx)if temp_fvalbest < fvalbest:fvalbest = temp_fvalbestxposbest = temp_xposbestbest_fval.append(fvalbest)return xposbest, fvalbest, best_fval# mu函数
def mu_fun(x, a, k, m):if x > a:return k * ((x - a) ** m)elif -a <= x <= a:return 0elif x < a:return k * ((-x - a) ** m)# 求解适应值
def get_function_result(fname, *args):result = -1if fname == "f1":def f1():return sum(args[0] ** 2)result = f1if fname == "f2":def f2():sum1 = 0sum2 = 1for i in range(len(args[0])):sum1 += abs(args[0][i])sum2 *= abs(args[0][i])return sum1 + sum2result = f2elif fname == "f3":def f3():sum1 = 0for i in range(len(args[0])):sum1 += abs(args[0][i]) ** (i + 1)return sum1result = f3elif fname == "f4":def f4():sum1 = 0sum2 = 0for i in range(len(args[0])):sum1 += args[0][i]for j in range(len(args[0])):sum2 += sum1 ** 2return sum2result = f4elif fname == "f5":def f5():return np.max(abs(args[0]))result = f5elif fname == "f6":def f6():sum1 = 0for i in range(len(args[0]) - 1):sum1 += (100 * ((args[0][i + 1] - (args[0][i] ** 2)) ** 2) + ((args[0][i] - 1) ** 2))return sum1result = f6elif fname == "f7":def f7():sum1 = 0for i in range(len(args[0])):sum1 += ((args[0][i] + 0.5) ** 2)return sum1result = f7elif fname == "f8":def f8():sum1 = 0for i in range(len(args[0])):sum1 += (i + 1) * (args[0][i] ** 4)return sum1 + np.random.random()result = f8elif fname == "f9":def f9():sum1 = 0sum2 = 0for i in range(len(args[0])):sum1 += args[0][i] ** 2sum2 += 0.5 * (i + 1) * args[0][i]return sum1 + sum2 ** 2 + sum2 ** 4result = f9elif fname == "f10":def f10():sum1 = 0for i in range(len(args[0])):sum1 += args[0][i] * np.sin(np.sqrt(abs(args[0][i])))return -sum1result = f10elif fname == "f11":def f11():sum1 = 0sum2 = 0for i in range(len(args[0])):sum1 += np.sin(args[0][i]) ** 2sum2 += args[0][i] ** 2return 1 + sum1 - np.exp(-sum2)result = f11elif fname == "f12":def f12():sum1 = 0for i in range(len(args[0])):sum1 += (args[0][i] ** 4) - 16 * (args[0][i] ** 2) + 5 * args[0][i]return 0.5 * sum1result = f12elif fname == "f13":def f13():sum1 = 0for i in range(len(args[0])):sum1 += (args[0][i] ** 2) - 10 * np.cos(2 * np.pi * args[0][i]) + 10return sum1result = f13elif fname == "f14":def f14():sum1 = 0sum2 = 0for i in range(len(args[0])):sum1 += args[0][i] ** 2sum2 += np.cos(2 * np.pi * args[0][i])return -20 * np.exp(-0.2 * np.sqrt(sum1 / len(args[0]))) - np.exp(sum2 / len(args[0])) + 20 + np.eresult = f14elif fname == "f15":def f15():sum1 = 0sum2 = 1for i in range(len(args[0])):sum1 += args[0][i] ** 2sum2 *= np.cos(args[0][i] / np.sqrt(i + 1))return sum1 / 4000 - sum2 + 1result = f15elif fname == "f16":def f16():sum1 = 0sum2 = 0sum3 = 0for i in range(len(args[0])):sum1 += np.sin(args[0][i]) ** 2sum2 += args[0][i] ** 2sum3 += np.sin(np.sqrt(abs(args[0][i]))) ** 2return (sum1 - np.exp(-sum2)) * np.exp(-sum3)result = f16elif fname == "f17":def f17():sum1 = 0sum2 = 0for i in range(len(args[0]) - 1):sum1 += ((0.25 * (args[0][i] + 1)) ** 2) * (1 + 10 * (np.sin(np.pi * (1 + 0.25 * (args[0][i + 1] + 1))) ** 2))for j in range(len(args[0])):sum2 += mu_fun(args[0][j], 10, 100, 4)return np.pi / len(args[0]) * (10 * (np.sin(np.pi * (1 + 0.25 * (args[0][0] + 1))) ** 2) + sum1 + (0.25 * (args[0][-1] + 1)) ** 2) + sum2result = f17elif fname == "f18":def f18():sum1 = 0sum2 = 0for i in range(len(args[0]) - 1):sum1 += ((args[0][i] - 1) ** 2) * (1 + np.sin(3 * np.pi * args[0][i + 1]) ** 2)for j in range(len(args[0])):sum2 += mu_fun(args[0][j], 5, 100, 4)return 0.1 * (np.sin(3 * np.pi * args[0][0]) ** 2 + sum1 + ((args[0][-1] - 1) ** 2) * (1 + np.sin(2 * np.pi * args[0][-1]) ** 2)) + sum2result = f18elif fname == "f19":def f19():sum2 = 0a = [[-32, -16, 0, 16, 32, -32, -16, 0, 16, 32, -32, -16, 0, 16, 32, -32, -16, 0, 16, 32, -32, -16, 0, 16,32],[-32, -32, -32, -32, -32, -16, -16, -16, -16, -16, 0, 0, 0, 0, 0, 16, 16, 16, 16, 16, 32, 32, 32, 32,32]]for i in range(25):sum1 = 0for j in range(len(args[0])):sum1 += (args[0][j] - a[j][i]) ** 6sum2 += 1 / ((i + 1) + sum1)return 1 / (1 / 500 + sum2)result = f19elif fname == "f20":def f20():sum1 = 0a = [0.1957, 0.1947, 0.1735, 0.16, 0.0844, 0.0627, 0.0456, 0.0342, 0.0323, 0.0235, 0.0246]b = 1 / np.asarray([0.25, 0.5, 1, 2, 4, 6, 8, 10, 12, 14, 16])for i in range(11):sum1 += abs(a[i] - (args[0][0] * (b[i] ** 2 + b[i] * args[0][1])) / (b[i] ** 2 + b[i] * args[0][2] + args[0][3])) ** 2return sum1result = f20elif fname == "f21":def f21():sum1 = 4 * (args[0][0] ** 2) - 2.1 * (args[0][0] ** 4) + (args[0][0] ** 6) / 3 + args[0][0] * args[0][1] - 4 * (args[0][1] ** 2) + 4 * (args[0][1] ** 4)return sum1result = f21elif fname == "f22":def f22():sum1 = 0a = [[4, 4, 4, 4], [1, 1, 1, 1], [8, 8, 8, 8], [6, 6, 6, 6], [3, 7, 3, 7], [2, 9, 2, 9], [5, 5, 3, 3],[8, 1, 8, 1], [6, 2, 6, 2], [7, 3.6, 7, 3.6]]c = [0.1, 0.2, 0.2, 0.4, 0.4, 0.6, 0.3, 0.7, 0.5, 0.5]for i in range(5):sum1 += 1 / abs(sum((args[0] - np.asarray(a[i])) ** 2) + c[i])return -sum1result = f22elif fname == "f23":def f23():sum1 = 0a = [[4, 4, 4, 4], [1, 1, 1, 1], [8, 8, 8, 8], [6, 6, 6, 6], [3, 7, 3, 7], [2, 9, 2, 9], [5, 5, 3, 3],[8, 1, 8, 1], [6, 2, 6, 2], [7, 3.6, 7, 3.6]]c = [0.1, 0.2, 0.2, 0.4, 0.4, 0.6, 0.3, 0.7, 0.5, 0.5]for i in range(7):sum1 += 1 / abs(sum((args[0] - np.asarray(a[i])) ** 2) + c[i])return -sum1result = f23elif fname == "f24":def f24():sum1 = 0a = [[4, 4, 4, 4], [1, 1, 1, 1], [8, 8, 8, 8], [6, 6, 6, 6], [3, 7, 3, 7], [2, 9, 2, 9], [5, 5, 3, 3],[8, 1, 8, 1], [6, 2, 6, 2], [7, 3.6, 7, 3.6]]c = [0.1, 0.2, 0.2, 0.4, 0.4, 0.6, 0.3, 0.7, 0.5, 0.5]for i in range(10):sum1 += 1 / abs(sum((args[0] - np.asarray(a[i])) ** 2) + c[i])return -sum1result = f24return result# 获取目标函数相关参数
def get_functions_details(fname):if fname == "f1":lb = -100ub = 100nd = 30fobj = lambda x: get_function_result("f1", x)return lb, ub, nd, fobjelif fname == "f2":lb = -10ub = 10nd = 30fobj = lambda x: get_function_result("f2", x)return lb, ub, nd, fobjelif fname == "f3":lb = -1ub = 1nd = 30fobj = lambda x: get_function_result("f3", x)return lb, ub, nd, fobjelif fname == "f4":lb = -100ub = 100nd = 30fobj = lambda x: get_function_result("f4", x)return lb, ub, nd, fobjelif fname == "f5":lb = -100ub = 100nd = 30fobj = lambda x: get_function_result("f5", x)return lb, ub, nd, fobjelif fname == "f6":lb = -30ub = 30nd = 30fobj = lambda x: get_function_result("f6", x)return lb, ub, nd, fobjelif fname == "f7":lb = -100ub = 100nd = 30fobj = lambda x: get_function_result("f7", x)return lb, ub, nd, fobjelif fname == "f8":lb = -1.28ub = 1.28nd = 30fobj = lambda x: get_function_result("f8", x)return lb, ub, nd, fobjelif fname == "f9":lb = -5ub = 10nd = 30fobj = lambda x: get_function_result("f8", x)return lb, ub, nd, fobjelif fname == "f10":lb = -500ub = 500nd = 30fobj = lambda x: get_function_result("f10", x)return lb, ub, nd, fobjelif fname == "f11":lb = -10ub = 10nd = 30fobj = lambda x: get_function_result("f11", x)return lb, ub, nd, fobjelif fname == "f12":lb = -5ub = 5nd = 30fobj = lambda x: get_function_result("f12", x)return lb, ub, nd, fobjelif fname == "f13":lb = -5.12ub = 5.12nd = 30fobj = lambda x: get_function_result("f13", x)return lb, ub, nd, fobjelif fname == "f14":lb = -32ub = 32nd = 30fobj = lambda x: get_function_result("f14", x)return lb, ub, nd, fobjelif fname == "f15":lb = -600ub = 600nd = 30fobj = lambda x: get_function_result("f15", x)return lb, ub, nd, fobjelif fname == "f16":lb = -10ub = 10nd = 30fobj = lambda x: get_function_result("f16", x)return lb, ub, nd, fobjelif fname == "f17":lb = -50ub = 50nd = 30fobj = lambda x: get_function_result("f17", x)return lb, ub, nd, fobjelif fname == "f18":lb = -50ub = 50nd = 30fobj = lambda x: get_function_result("f18", x)return lb, ub, nd, fobjelif fname == "f19":lb = -65.536ub = 65.536nd = 2fobj = lambda x: get_function_result("f19", x)return lb, ub, nd, fobjelif fname == "f20":lb = -5ub = 5nd = 4fobj = lambda x: get_function_result("f20", x)return lb, ub, nd, fobjelif fname == "f21":lb = -5ub = 5nd = 2fobj = lambda x: get_function_result("f21", x)return lb, ub, nd, fobjelif fname == "f22":lb = 0ub = 10nd = 4fobj = lambda x: get_function_result("f22", x)return lb, ub, nd, fobjelif fname == "f23":lb = 0ub = 10nd = 4fobj = lambda x: get_function_result("f23", x)return lb, ub, nd, fobjelif fname == "f24":lb = 0ub = 10nd = 4fobj = lambda x: get_function_result("f24", x)return lb, ub, nd, fobjif __name__ == '__main__':# 白鲸种群数out_n = 50# 最大迭代次数out_tmax = 1000# 目标函数out_fobj = "f22"# 获取函数参数out_lb, out_ub, out_nd, out_fobj = get_functions_details(out_fobj)out_xposbest, out_fvalbest, out_best_fval = bwo(out_n, out_tmax, out_lb, out_ub, out_nd, out_fobj)# 画图plt.plot(range(len(out_best_fval)), out_best_fval)plt.xlabel("t")plt.ylabel("best value")plt.show()print("xposbest = ", out_xposbest)print("fvalbest = ", f"{out_fvalbest: .5f}")
白鲸优化算法有哪些应用场景:
白鲸优化算法可以应用于各种优化问题,包括但不限于函数优化、约束优化、多目标优化等。具体的应用场景包括但不限于:
工程优化:白鲸优化算法可以用于机械设计、电力系统、交通运输等领域的优化问题,如结构优化设计、输电线路布局优化、公交车线路优化等。
无线通信优化:白鲸优化算法可以用于无线传感器网络的布局和能量管理,以及无线信道分配和频谱分配等优化问题。
图像处理:白鲸优化算法可以用于图像处理中的参数选择和优化问题,如图像去噪、图像增强等。
总之,白鲸优化算法可以应用于各种需要寻找最优解的问题,通过全局搜索和局部搜索的平衡,找到问题的最优解。
参考资料
https://mp.weixin.qq.com/s/vGcZ1_Bh4M5_CcuCclWt5Q
https://blog.csdn.net/jiaheming1983/article/details/129632261
https://blog.csdn.net/qq_41851955/article/details/127360805
这篇关于【启发式算法】白鲸优化算法【附python实现代码】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







