sklearn机器学习：支持向量机(SMV)

关于支持向量机的原理部分本人阅读的是李航《统计学习方法》，自己也做了个学习笔记，移步线性可分支持向量机，线性支持向量机，非线性支持向量机与SMO算法。以下注重sklearn中SVM部分的代码学习，不会过多的介绍原理。会涉及到SVM的简单使用，4种核函数，SVM的参数，调参以及一些接口属性的介绍。

先来创建个数据集，可视化后再来使用SVM

import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import make_blobs
import numpy as np
#创建数据，500个样本，标签两类0,1。默认特征2个
X,y = make_blobs(n_samples=500,centers=2)
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size = 0.5)#训练集和测试集划分
plt.scatter(Xtrain[:,0],Xtrain[:,1],c=Ytrain,cmap="rainbow")
plt.show()

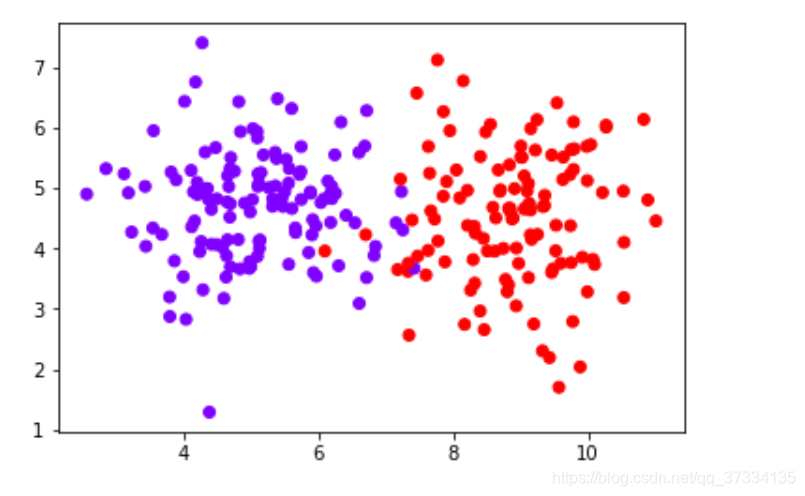
svm初步使用   这也太厉害了
from sklearn.svm import SVC
svm = SVC(kernel="linear").fit(Xtrain,Ytrain)
svm.score(Xtest,Ytest)

输出：0.976

来探索一下属性和接口

#使用乳腺癌数据集
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
X = data.data
y = data.target
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size = 0.3)
svm = SVC(kernel="linear").fit(Xtrain,Ytrain)
svm.score(Xtest,Ytest)#返回给定测试数据和标签的平均准确度

输出：0.9415204678362573

1-(svm.predict(Xtest)!=Ytest).sum()/len(svm.predict(Xtest))#对测试数据进行预测

输出：0.9415204678362573

svm.support_vectors_ #支持向量
len(svm.support_vectors_),svm.n_support_ #支持向量个数

输出：(40, array([19, 21]))

在非线性数据集上来使用SVM

#在非线性数据集上来看效果
from sklearn.datasets import make_circles
X,y = make_circles(n_samples=500,noise=0.1,factor=0.1)#两个特征，二维
plt.scatter(X[:,0],X[:,1],c=y,cmap="rainbow")
plt.show()

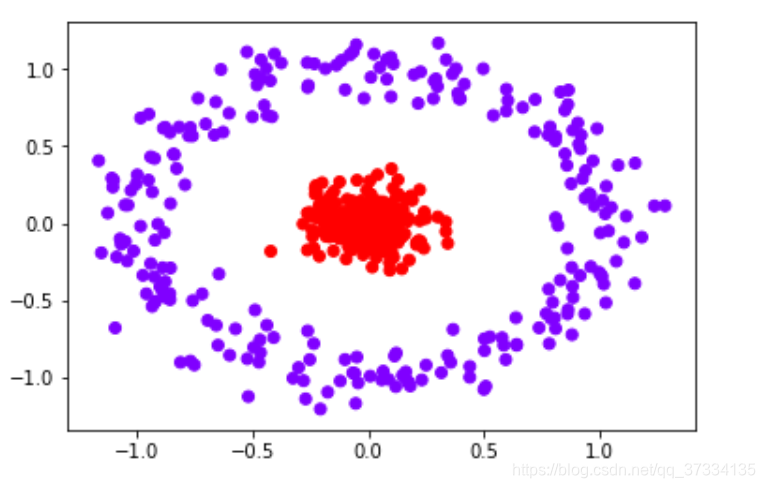
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size = 0.3)svm = SVC(kernel="linear").fit(Xtrain,Ytrain)
svm.score(Xtest,Ytest)

输出：0.5466666666666666，这个结果真是太糟糕了，再看参数kernel=“linear”，看名字知道使用的核函数是线性核函数，也就是使用的线性支持向量机，所以对非线性的分类效果不好，实际上对图形进行升维，升到3维，让上面的图称为三维图的俯瞰图，此时在两者之间就能找出个超平面了，此时再去使用线性支持向量机去拟合效果就很好了，这个过程称为核技巧。但是维度过高计算会很慢，所以可以引入核函数，在原来的维度空间进行计算。下面是参数kernel选择项

其中sigmoid中的tanh指的是sigmoid函数$\frac{1}{1+e^{-x}}$
那么到底选哪个输入呢？
来探索在不同数据集上不同的核函数的表现

#不同的核函数在不同的数据集上的表现
from sklearn.datasets import make_blobs,make_circles,make_moons,make_classification
n = 500
datasets = [make_moons(n_samples=n, noise=0.2),make_circles(n_samples=n, noise=0.2, factor=0.5),make_blobs(n_samples=n, centers=2),make_classification(n_samples=n,n_features =2,n_informative=2,n_redundant=0)]
kernel = ["linear","rbf","poly","sigmoid"]
names = ["moons","circles","blobs","classification"]
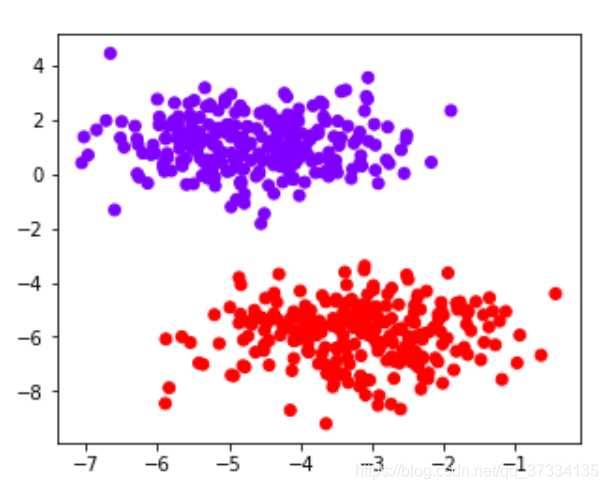
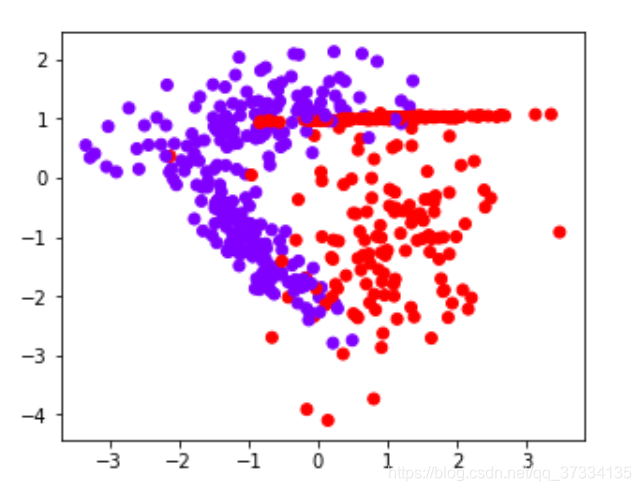
for X,y in datasets:plt.figure(figsize=(10,8))plt.scatter(X[:,0],X[:,1],c=y,cmap="rainbow")
plt.show()

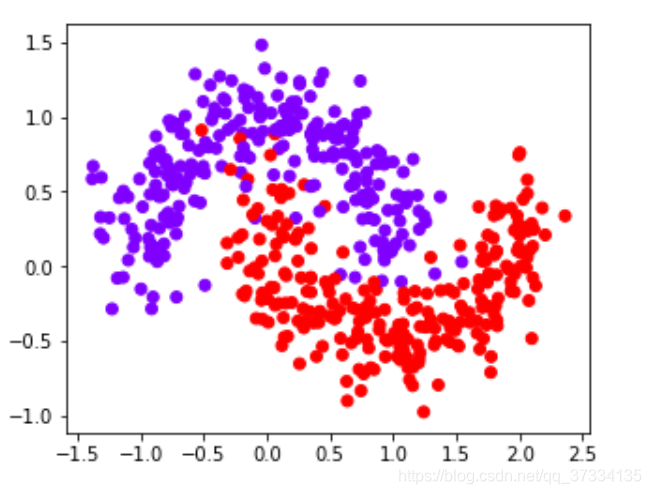
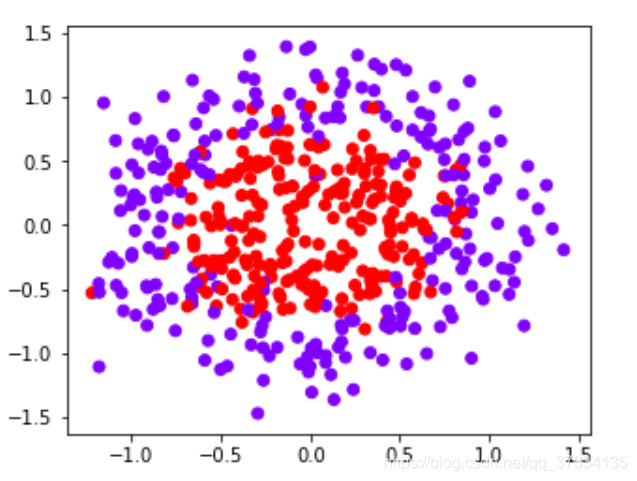
for i,data in enumerate(datasets):print(names[i]+"==============================")X,y = dataXtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size = 0.3)for j in kernel:svm = SVC(kernel=j,degree=1, cache_size=5000,gamma="auto").fit(Xtrain,Ytrain)print(j,svm.score(Xtest,Ytest))

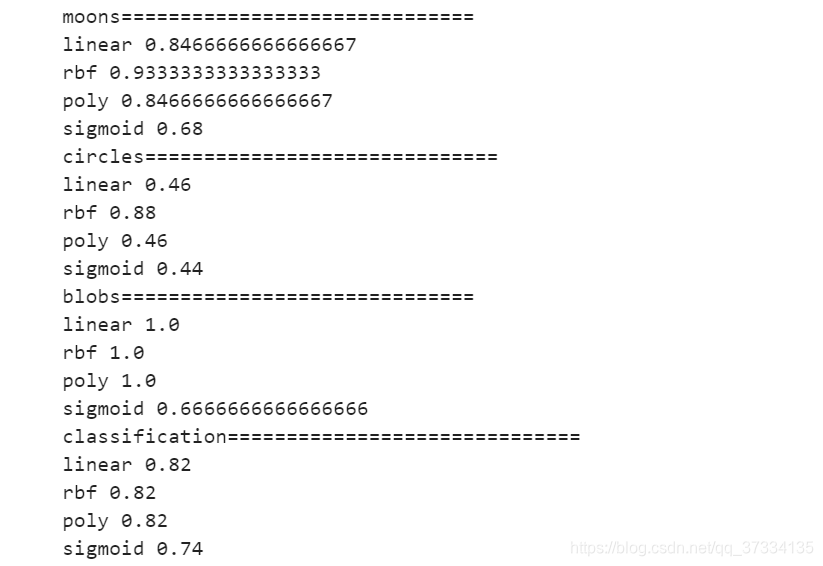
从输出来看，rbf的效果都是相当不错的；在线性数据集上linear和poly都表现的不错，但是在非线性数据集上表现的不尽人意；再看sigmoid真是表现的糟糕。

再来看几个核函数在乳腺癌数据集上的表现（线性数据集）

#探索核函数的优势和缺陷
from sklearn.datasets import load_breast_cancer
data = load_breast_cancer()
X = data.data
y = data.targetplt.scatter(X[:,0],X[:,1],c=y)
plt.show()

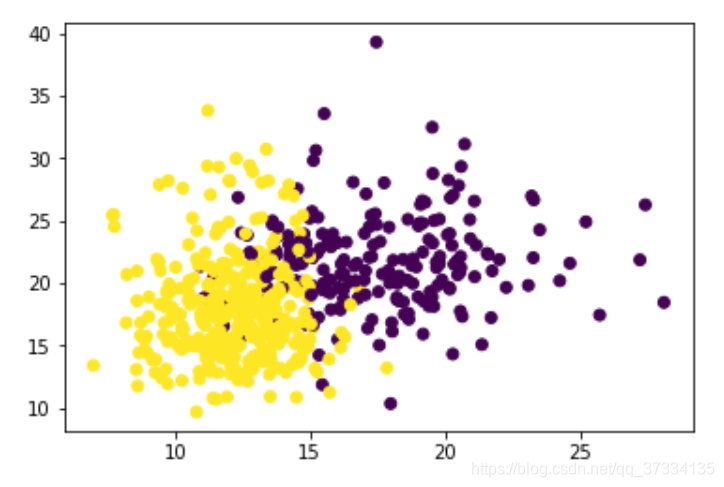
from time import time
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size = 0.3)
kernel = ["linear","rbf","poly","sigmoid"]
for i in kernel:
t = time()
svm = SVC(kernel=i,gamma="auto",degree=1,cache_size=5000).fit(Xtrain,Ytrain)
print(i,svm.score(Xtest,Ytest),time()-t)

为什么rbf上表现的会这么糟糕呢？前面不是说rbf在各种数据集上都表现的不错嘛，探索下数据

#量纲统一
import pandas as pd
d = pd.DataFrame(X)
d.describe([0.01,0.05,0.1,0.25,0.5,0.75,0.9,0.99]).T

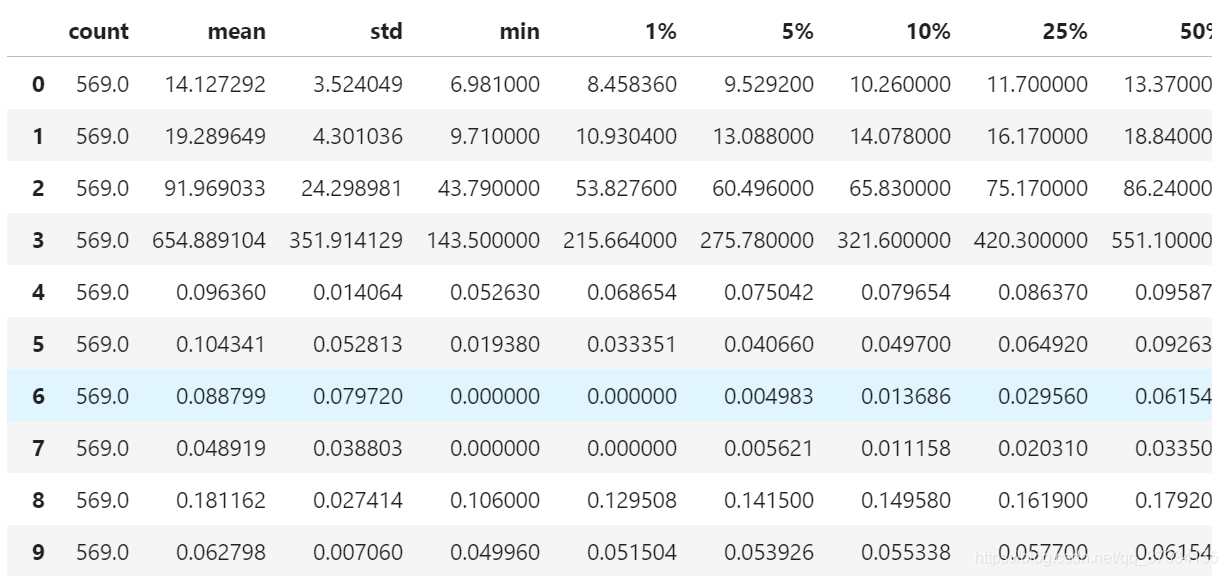
可以发现，均值，方差与最小值都存在量纲不统一问题，也就是有的特征的值很小而有的过大，比如均值有的是0.04而有的是654。在数据是99%的时候与最大值比较发现也有差异很大的也就是存在偏态（不是正态分布）。我们对数据进行标准化

from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(X)
pd.DataFrame(X).describe().T
from time import time
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,y,test_size = 0.3)
kernel = ["linear","rbf","poly","sigmoid"]
for i in kernel:
t = time()
svm = SVC(kernel=i,gamma="auto",degree=1,cache_size=5000).fit(Xtrain,Ytrain)
print(i,svm.score(Xtest,Ytest),time()-t)#模型运行时间也大大缩短了

发现rbf对应的输出值明显增大了，而且所有的核函数对应的时间都减小了，尤其线性核函数，之前运行需要2.89秒，说明了rbf核函数不擅长处理量纲不统一的数据集。

幸运的是，这个缺点都可以由数据无量纲化来解决。因此，SVM执行之前，非常推荐先进行数据的无量纲化！到了这一步，我们是否已经完成建模了呢？虽然线性核函数的效果是最好的，但它是没有核函数相关参数可以调整的，rbf和多项式却还有着可以调整的相关参数，接下来我们就来看看这些参数。

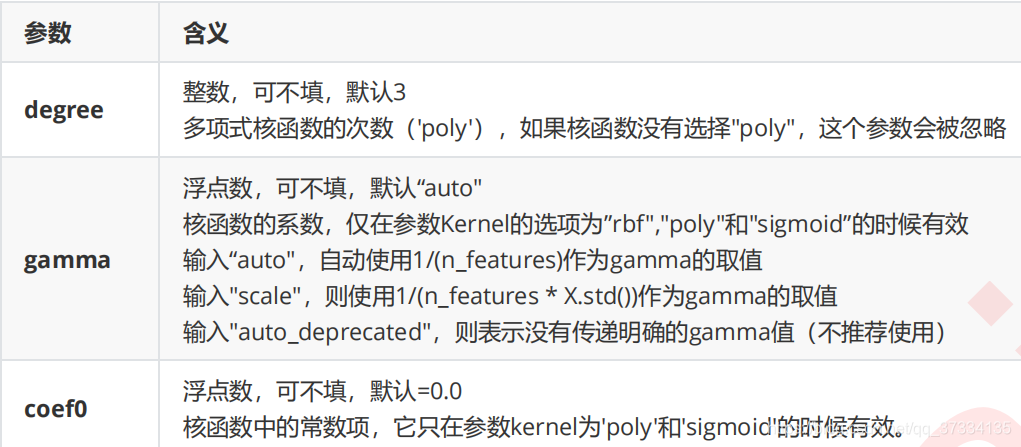
从前面的表中对于linear核函数是没有可以调的参数的（只针对上述的表中参数），对于rbf核函数可以调参数gamma，我们通过学习曲线来看

#rbf的参数gamma
score = []
gamma = np.logspace(-10,1,50)
for i in gamma:svm = SVC(kernel="rbf",gamma=i,cache_size=5000).fit(Xtrain,Ytrain)score.append(svm.score(Xtest,Ytest))
print(max(score),gamma[score.index(max(score))])
plt.plot(gamma,score)
plt.show()

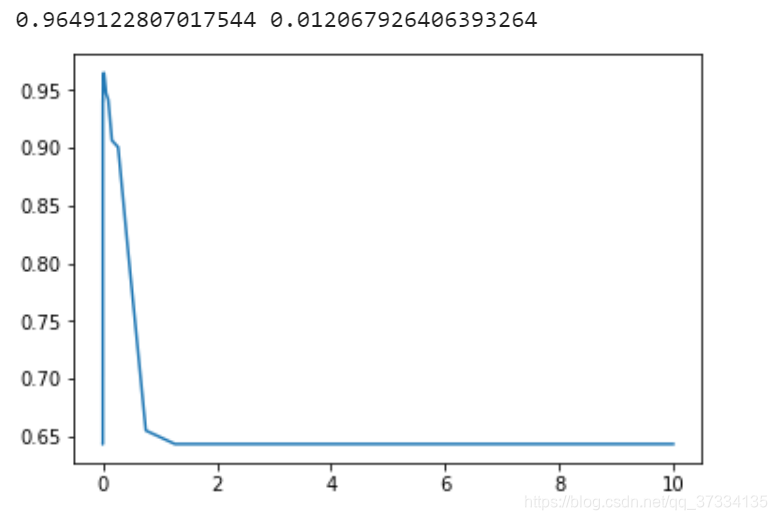
当ganmma=0.0120679的时候，相比之前的结果是有所提升的，那么就选这个值。再来调poly参数，三个参数均可以调，但是对于degree也就是多项式中的d，这个值如果对于前面测试的数据集，设置了d=3发现就跑不出结果了，由于线性数据集就设置为1吧。所以可以调的参数就2个，这里使用网格搜索。

#poly  网格搜索
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import StratifiedShuffleSplit
gamma_range = np.logspace(-10,1,20)
coef0_range = np.linspace(0,5,10)
param = dict(gamma = gamma_range,coef0=coef0_range)
cv = StratifiedShuffleSplit(n_splits=5,test_size=0.3)
grid = GridSearchCV(SVC(kernel="poly"),param_grid=param,cv=10)
grid.fit(X,y)
grid.best_params_,grid.best_score_

输出：({‘coef0’: 3.8888888888888893, ‘gamma’: 0.012742749857031322},
0.9789103690685413)

注意到，乳腺癌数据不是线性可分的，即存在噪音，需要加入惩罚项，实际上默认参数C是等于1的（具体的值看应用，C越大惩罚力度越大，反之成都力度越小），那么接下来就来调这个参数

#参数C 探索rbf核函数
score = []
C = np.linspace(0.01,20,100)
for i in C:svm = SVC(kernel="rbf",C=i,gamma=0.012067926406393264,cache_size=5000).fit(Xtrain,Ytrain)score.append(svm.score(Xtest,Ytest))
print(max(score),C[score.index(max(score))])
plt.plot(C,score)
plt.show()

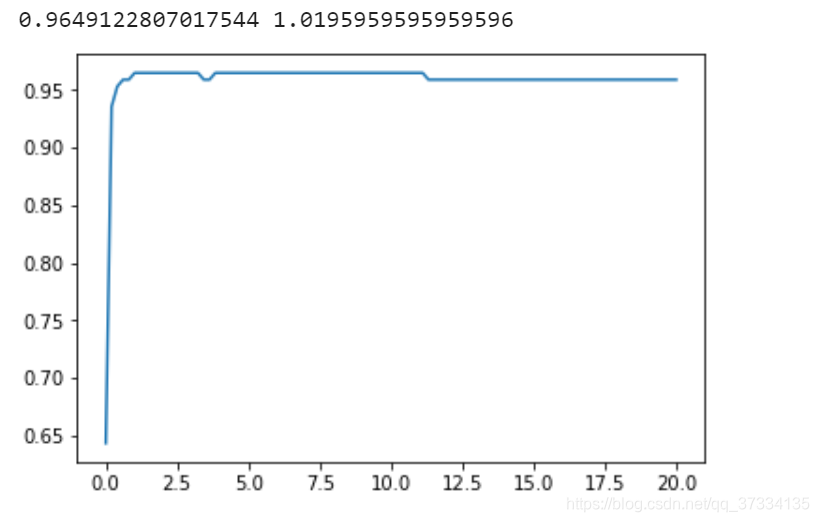
好像并没有提升

#参数C  探索线性核函数
score = []
C = np.linspace(0.01,20,100)
for i in C:svm = SVC(kernel="linear",C=i,cache_size=5000).fit(Xtrain,Ytrain)score.append(svm.score(Xtest,Ytest))
print(max(score),C[score.index(max(score))])
plt.plot(C,score)
plt.show()

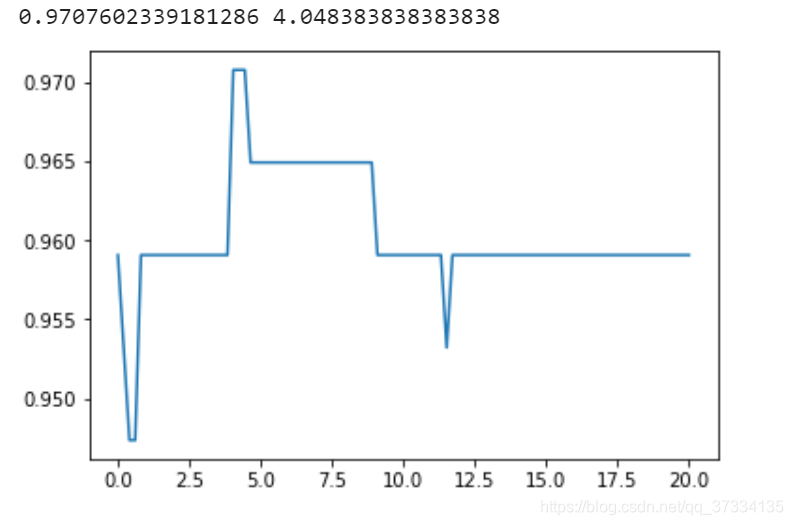
这个显然就提升了。