机器学习之——多项式回归与degree参数调节

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression 

1.读取数据

# data = pd.read_csv('job.csv')
# data = np.loadtxt('job.csv', delimiter=',')
data = np.genfromtxt('job.csv', delimiter=',')
# print(data)

2.特征

X_data = data[1:, 1]

3.标签

y_data = data[1:, 2]
# print(X_data)

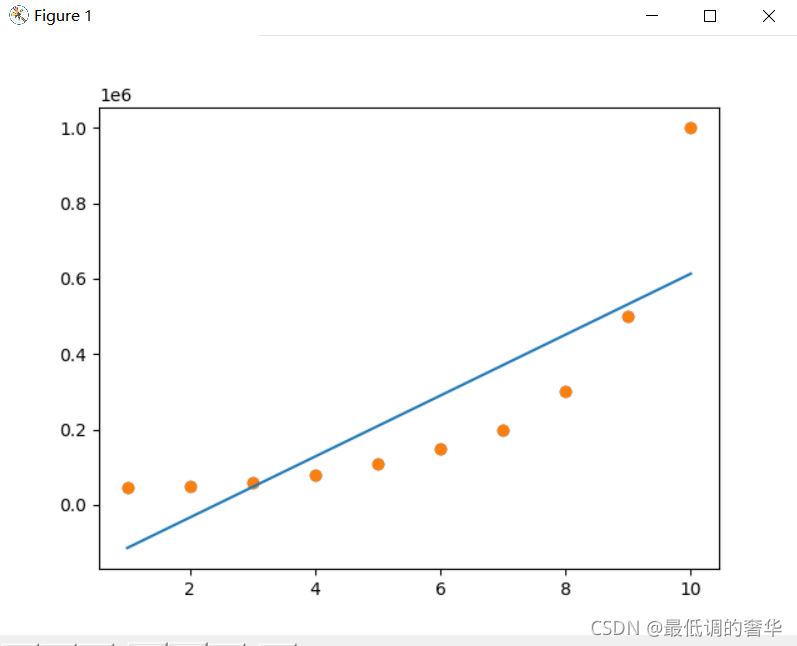
4.可视化（先以线性方程来预测）

plt.scatter(X_data, y_data)
# plt.show()

5. 建模

X_data 转为二维数组对象

X_data = X_data[:, np.newaxis]
model = LinearRegression()
model.fit(X_data, y_data)plt.scatter(X_data, y_data)
plt.plot(X_data, model.predict(X_data))
plt.show()

1.将数据处理为多项式回归

from sklearn.preprocessing import PolynomialFeatures

2. 创建多项式对象

poly_reg = PolynomialFeatures(degree=5)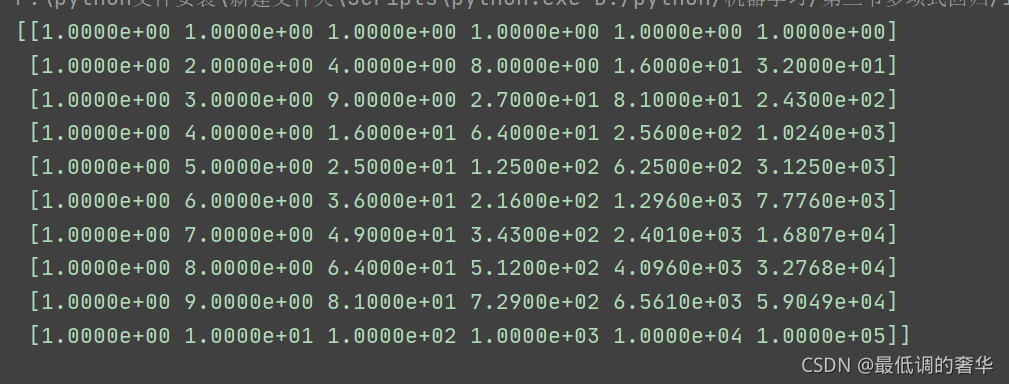

3. 数据处理

x_poly = poly_reg.fit_transform(X_data)
print(x_poly)line_reg = LinearRegression()
line_reg.fit(x_poly, y_data)
plt.scatter(X_data, y_data, color='r')plt.plot(X_data, line_reg.predict(x_poly))
plt.show()

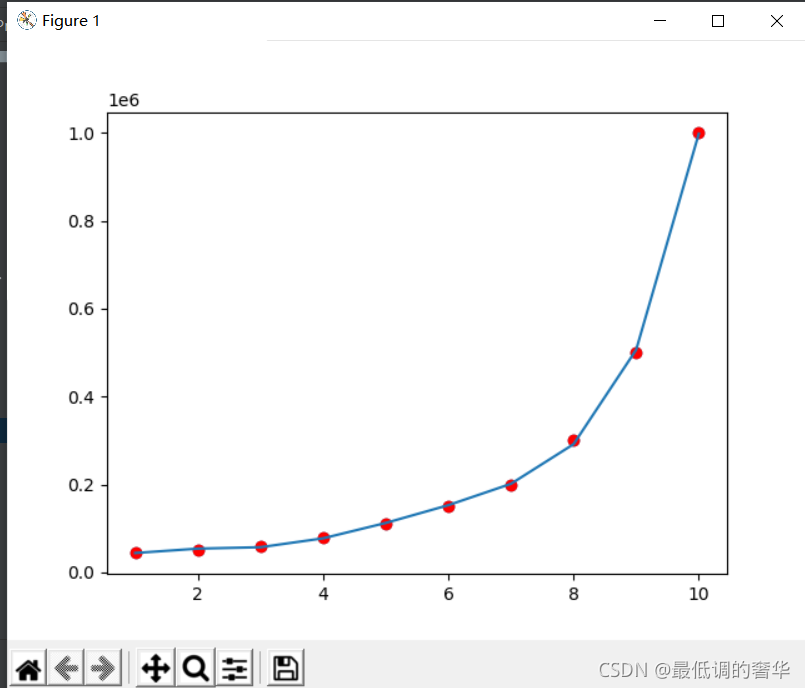
3.多项式回归模型构建和预测

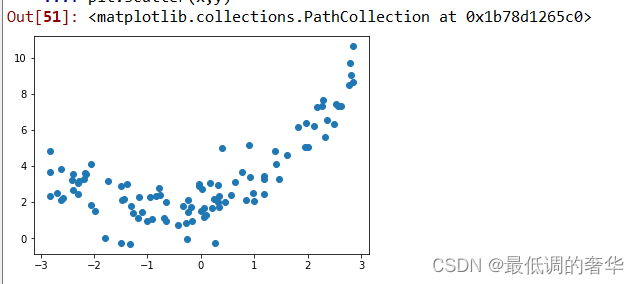
• 1.创建数据查看数据分布

import matplotlib.pyplot as plt 
import numpy as np
import pandas as pda = np.random.uniform(-3.0,3.0,size=100) 
x = a.reshape(-1,1)y = 0.5*a**2 + a + 2 + np.random.normal(0,1,size=100)plt.scatter(x,y)

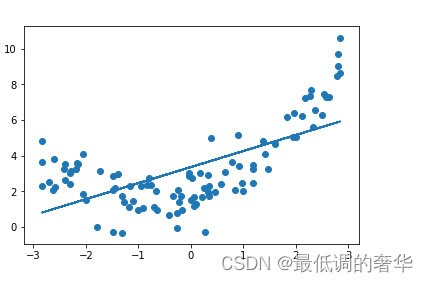
• 2.线性回归模型预测

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(x,y)n = lin_reg.predict(x)
plt.plot(x,n)
plt.scatter(x,y)
plt.show()

• 3.查看模型评分

lin_reg.score(x,y)
>>0.4193432238155308

• 4.查看均方误差

from sklearn.metrics import mean_squared_error
mean_squared_error(y,n)
>> 3.0695392007737921

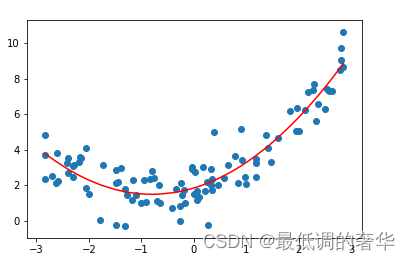
• 5.2次多项式回归建立
• degree越大，模型的拟合效果越好，均方误差越小，因为样本是一定的，我们总能找到一条曲线将所有的样本点拟合，也就是说让所有的样本点都落到这条线上，使整体均方误差为0，而如果对未知的待预测的数据预测过程中，过量拟合训练集会造成泛化能力降低，预测偏差增大，所以说，并不是degree越大预测的越准确。
• 封装Pipeline管道，便于灵活调整多项式回归模型参数

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScalerdef kk(degree):return Pipeline([('poly',PolynomialFeatures(degree=degree)),('std_scaler',StandardScaler()),('lin_reg',LinearRegression())])model = kk(degree=2)
model.fit(x,y)
d = model.predict(x)plt.plot(np.sort(x,axis=0),d[np.argsort(x,axis=0)],color='r')
plt.scatter(x,y)
plt.show()

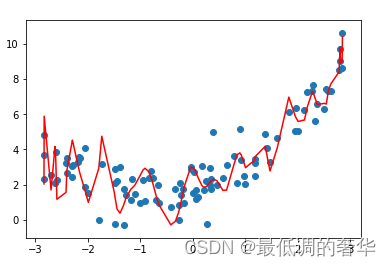
• 6.50次多项式回归

def kk(degree):return Pipeline([('poly',PolynomialFeatures(degree=degree)),('std_scaler',StandardScaler()),('lin_reg',LinearRegression())])model = kk(degree=50)
model.fit(x,y)
d = model.predict(x)plt.plot(np.sort(x,axis=0),d[np.argsort(x,axis=0)],color='r')
plt.scatter(x,y)
plt.show()

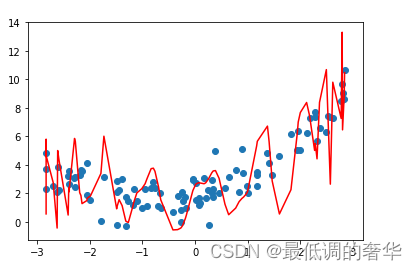
• 7.200次多项式回归

def kk(degree):return Pipeline([('poly',PolynomialFeatures(degree=degree)),('std_scaler',StandardScaler()),('lin_reg',LinearRegression())])model = kk(degree=200)
model.fit(x,y)
d = model.predict(x)plt.plot(np.sort(x,axis=0),d[np.argsort(x,axis=0)],color='r')
plt.scatter(x,y)
plt.show()