本文主要是介绍编译原理(三)语法分析:4.上下文有关CSG、CSL和形式语言,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、上下文有关文法CSG
- 1.引入原因
- 2.CSL
- 二、形式语言
- 1.定义
- 2.特点
【编译原理博客列表】》》》》》》
一、上下文有关文法CSG
1.引入原因
程序设计语言中除了CFG可以描述的结构之外,还有一些是CFG无法描述的所谓上下文有关的结构。典型的这类语言结构包括:变量的声明与引用、过程调用时形参与实参的一致性检查等。所以引入上下文有关文法(Context Sensitive Grammar, CSG)
例3.12 不能用CFG描述的语言,得用CSL描述的
L 1 = { ω c ω ∣ ω ∈ ( a ∣ b ) ∗ } L1=\{ωcω|ω∈(a|b)*\} L1={ωcω∣ω∈(a∣b)∗} (标识符声明与引用一致性的抽象)
L 2 = { a n b m c n d m ∣ n ≥ 1 和 m ≥ 1 } L2=\{a^nb^mc^nd^m|n≥1和m≥1\} L2={anbmcndm∣n≥1和m≥1} (形参与实参一致性的抽象)
L 3 = { a n b n c n ∣ n ≥ 1 } L3=\{a^nb^nc^n|n≥1\} L3={anbncn∣n≥1} (计数问题的抽象,要考【CSL复杂度低,就一个】)
相近的、可以用CFL描述的
L 1 ′ = { ω c ω r ∣ ω ∈ ( a ∣ b ) ∗ } L1'=\{ωcω^r|ω∈(a|b)*\} L1′={ωcωr∣ω∈(a∣b)∗}(S→aSa|bSb|c)
L 2 ′ = { a n b m c m d n ∣ n ≥ 1 , m ≥ 1 } L2'=\{a^nb^mc^md^n|n≥1, m≥1\} L2′={anbmcmdn∣n≥1,m≥1}(S→aSd|aAd,A→bAc|bc)
L 2 ′ ′ = { a n b n c m d m ∣ n ≥ 1 , m ≥ 1 } L2''=\{a^nb^nc^md^m|n≥1, m≥1\} L2′′={anbncmdm∣n≥1,m≥1}(S→AB,A→aAb|ab,B→cBd|cd)
L 3 ′ = { a m b m c n ∣ m , n ≥ 1 } L3'=\{a^mb^mc^n|m, n≥1\} L3′={ambmcn∣m,n≥1}(S→AC,A→aAb|ab,C→cC|c)(计数问题的抽象,要考【CFL复杂度高,则两个】)
2.CSL
CSG产生的语言就是CSL
二、形式语言
1.定义
定义3.8
若文法G=(N,T,P,S)的每个产生式α→β中,均有 α ∈ ( N ∪ T ) ∗ α∈(N∪T)* α∈(N∪T)∗,且至少含有一个非终结符, β ∈ ( N ∪ T ) ∗ β∈(N∪T)* β∈(N∪T)∗,则称G为0型文法。
对0型文法施加以下第i条限制,即得到i型文法。
①G的任何产生式α→β(S→ε除外)满足 ∣ α ∣ ≤ ∣ β ∣ |α|≤|β| ∣α∣≤∣β∣;
②G的任何产生式形如A→β,其中A∈N, β ∈ ( N ∪ T ) ∗ β∈(N∪T)* β∈(N∪T)∗;
③G的任何产生式形如A→a或者A→aB(或者A→Ba),其中A和B∈N,a∈T。
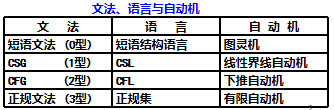
2.特点
结论:CSG、CFG、正规式能力递减
但是:能力越强的文法,其文法的设计和自动机的构造越困难
因此:语法分析仅用到CFG(除特别指出,文法即指CFG )
这篇关于编译原理(三)语法分析:4.上下文有关CSG、CSL和形式语言的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





