天线基础参数:增益与方向性系数、方向性函数的区别与联系

天线是作为一种可以将导行电磁波和自由空间电磁波之间的转换器件，广泛用于接收或发射电磁波。为了评价天线的性能，也相应的定义了一些有关天线的基础参数如:方向性函数、方向性系数、增益等。下面来简要介绍一下这几个参数之间的区别与联系

1、方向性函数$F(\theta ,\phi )$

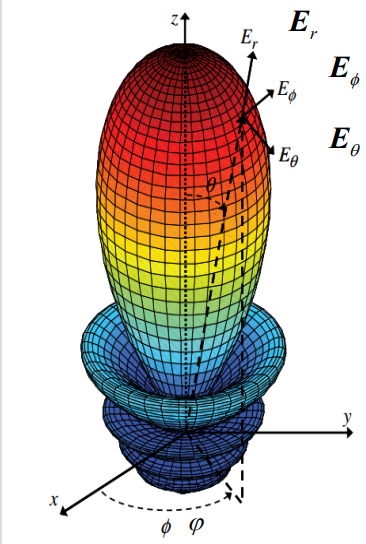
方向性函数描述了在距离天线r处的远区场电场强度幅值$|E=(\theta ,\phi )|$与辐射最强方向上距离天线r处的电场强度幅值$|E_{max}|$之比，描述了天线辐射的电场强度在空间中的相对分布情况，表达式如下：
$$F(\theta ,\phi )=\frac{|E=(\theta ,\phi )|}{|E_{max}|}$$

2、方向性系数$D(\theta ,\phi )$

方向性系数描述了在距离天线r处的远区场功率密度$S(\theta ,\phi )$与辐射功率$P_r$相同的理想无方向性天线在相同位置的功率密度 $S_0$之比。方向性系数定量描述了天线方向性的强弱。表达式如下：
$$D(\theta ,\phi )=\frac{S(\theta ,\phi )}{S_0}$$
或$$D(\theta ,\phi )=\frac{|{E=(\theta ,\phi )|}^2}{{|E_0|}^2}$$

3、方向性函数$F(\theta ,\phi )$与方向性系数$D(\theta ,\phi )$关系

假设天线任意方向辐射功率密度为：
$$S(\theta ,\phi )=\frac{|{E=(\theta ,\phi )|}^2}{2{\eta }_0}$$
${\eta }_0$为真空中波阻抗：
$${\eta }_0=20\pi \sqrt{\frac{{\mu }_0}{{\epsilon }_0}}=120\pi$$
求得半径为 的球面上的功率为:

$$\begin{array}{rl}{P}_r& ={\oint }_{s}S(\theta ,\phi )dS\\ & =\frac{r^2{|E_{max}|}^2}{2{\eta }_0}{\int }_0^{2\pi \pi }{\int }_0{F(\theta ,\phi )}^{2}sin\theta d\theta d\phi \end{array}$$
$$S_0=\frac{P_r}{4\pi r^2}$$
$$D(\theta ,\phi )=\frac{4\pi F^2(\theta ,\phi )}{{\int }_0^{2\pi \pi }{\int }_0{F(\alpha ,\beta )}^{2}sin\alpha d\alpha d\beta }$$

4、增益$G(\theta ,\phi )$

在距离天线r处的远区场功率密度$S(\theta ,\phi )$与输入功率$P_{in}$相同的理想无方向性天线在相同位置的功率密度$S_0$之比。可以看出，增益的定义与方向性系数的定义类似，与方向性系数一样，增益也可以用于表征天线方向性强弱。
$$G(\theta ,\phi )=\frac{S(\theta ,\phi )}{S_0}$$
或$$G(\theta ,\phi )=\frac{|{E=(\theta ,\phi )|}^2}{{|E_0|}^2}$$

5、增益$G(\theta ,\phi )$与方向性系数$D(\theta ,\phi )$关系

需要明确的是，增益计算的前提条件为输入功率$P_{in}$相同，而方向性系数的前提条件是辐射功率$P_r$相同这一点是需要注意的。