AK F.*ing leetcode 流浪计划之delaunay三角化

本文主要是介绍AK F.*ing leetcode 流浪计划之delaunay三角化，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

本期话题：给定二维点进行delaunay三角化
参考资料：

算法步骤与框架：
https://oi-wiki.org//geometry/triangulation/

空圆性深入解析：
【数字几何处理-中国科学技术大学-傅孝明】 【精准空降到 30:01】 https://www.bilibili.com/video/BV1B54y1B7Uc/?p=22&share_source=copy_web&vd_source=34b56bf81008e2621fca75c5166324c2&t=1801

定义

在数学和计算几何中，对于给定的平面中的离散点集 P，其 Delaunay 三角剖分 ，符号表示 为DT(P)，应该满足：

1. 三角部分后最外边界是一个凸包。
2. 空圆性：在 DT(P) 中，任意三角形的外接圆范围内不会有其它点存在。

算法过程

大概步骤

1. 排序: 对所有点按照x, y数值从小到大排序
2. 分治: 如果小2个点则直接加入边，否则继续分治
3. 合并：1)先找到一条基线（基线两点分别取待合并点集各一个），不与任何已经有边相交，如果有多条基线重合，则基线长越短越好。2）从基线2端点出发，找到直接相邻且邻边与基线夹角小于180的点作为候选点，如果没有候选点，则算法结束。3）从候选点中选出一个点（选中点）使得该点与基线两点的外接圆中不包含任意其他点（共圆除外）。4）添加一条边(ed), ed两端为选中点和基线中与选中点非同侧的点。5）删除与ed相交的所有边。更新基线一端为选中点，回到步骤2。

合并例子演示

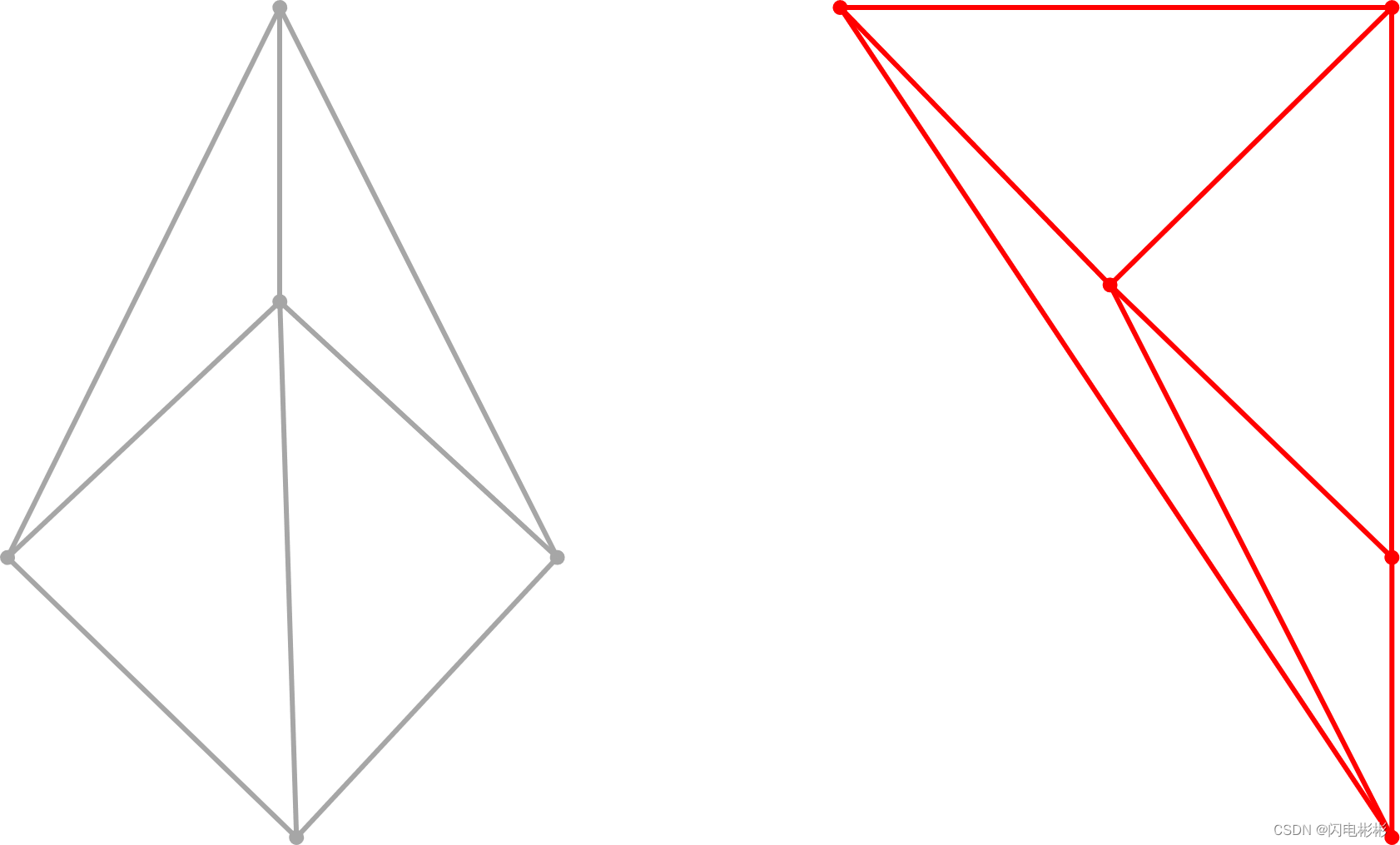
现在左右两边各自已经合并完成，需要整体合并。

1 找基线
具体查找方法在实现细节展示

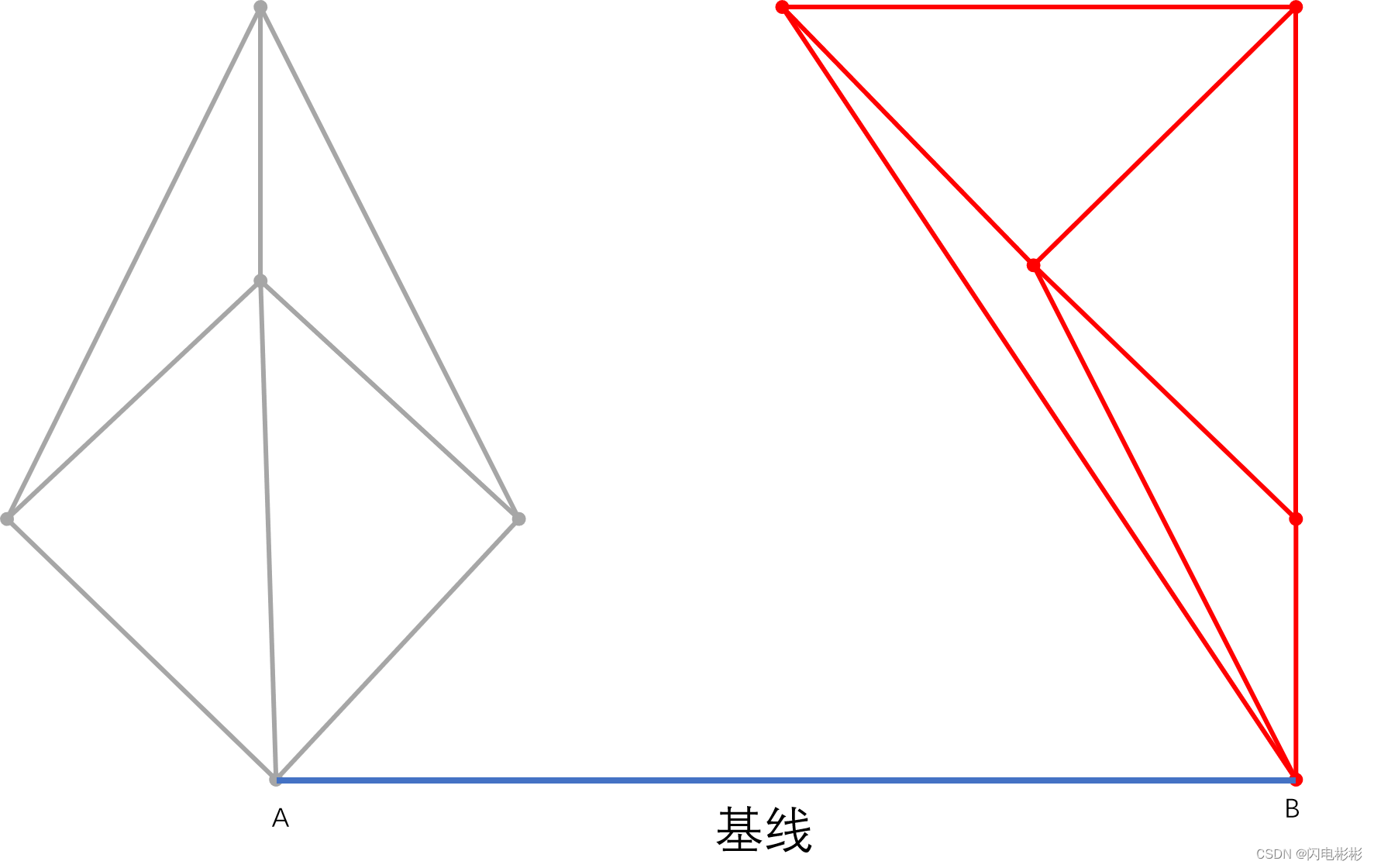
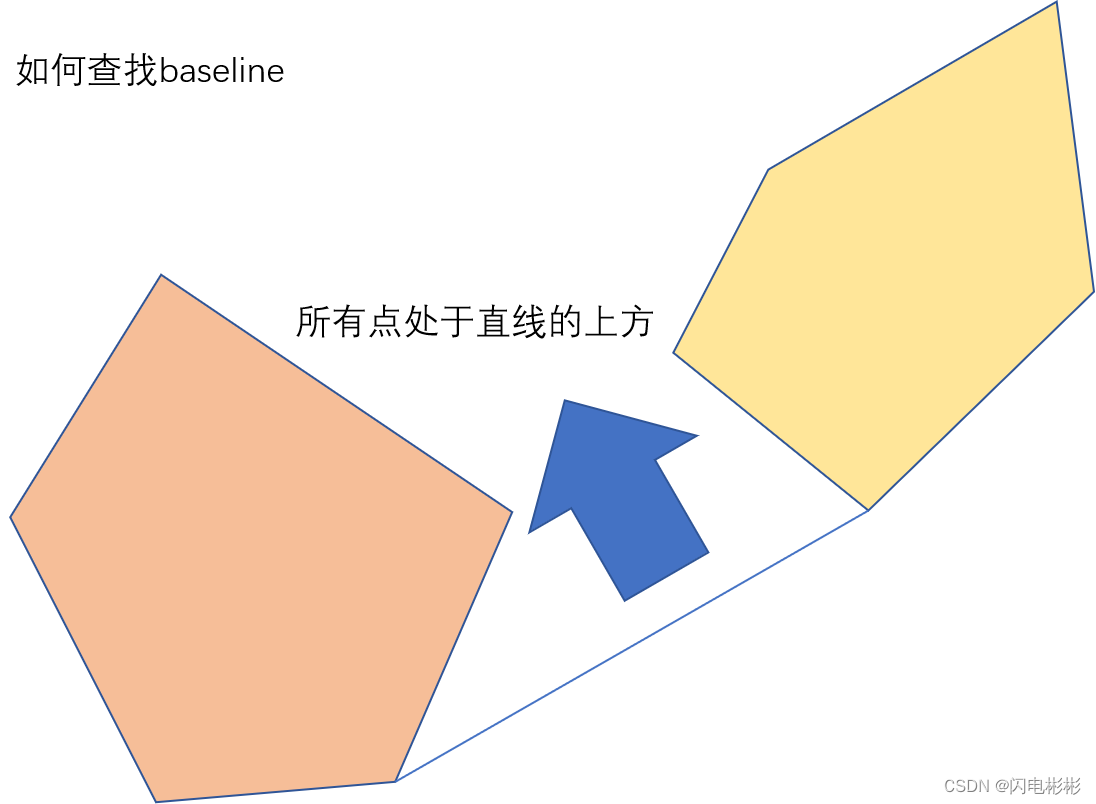
基线两点A, B分别位于左右两侧点集中。且所有点都处于基线上方。

2 候选点

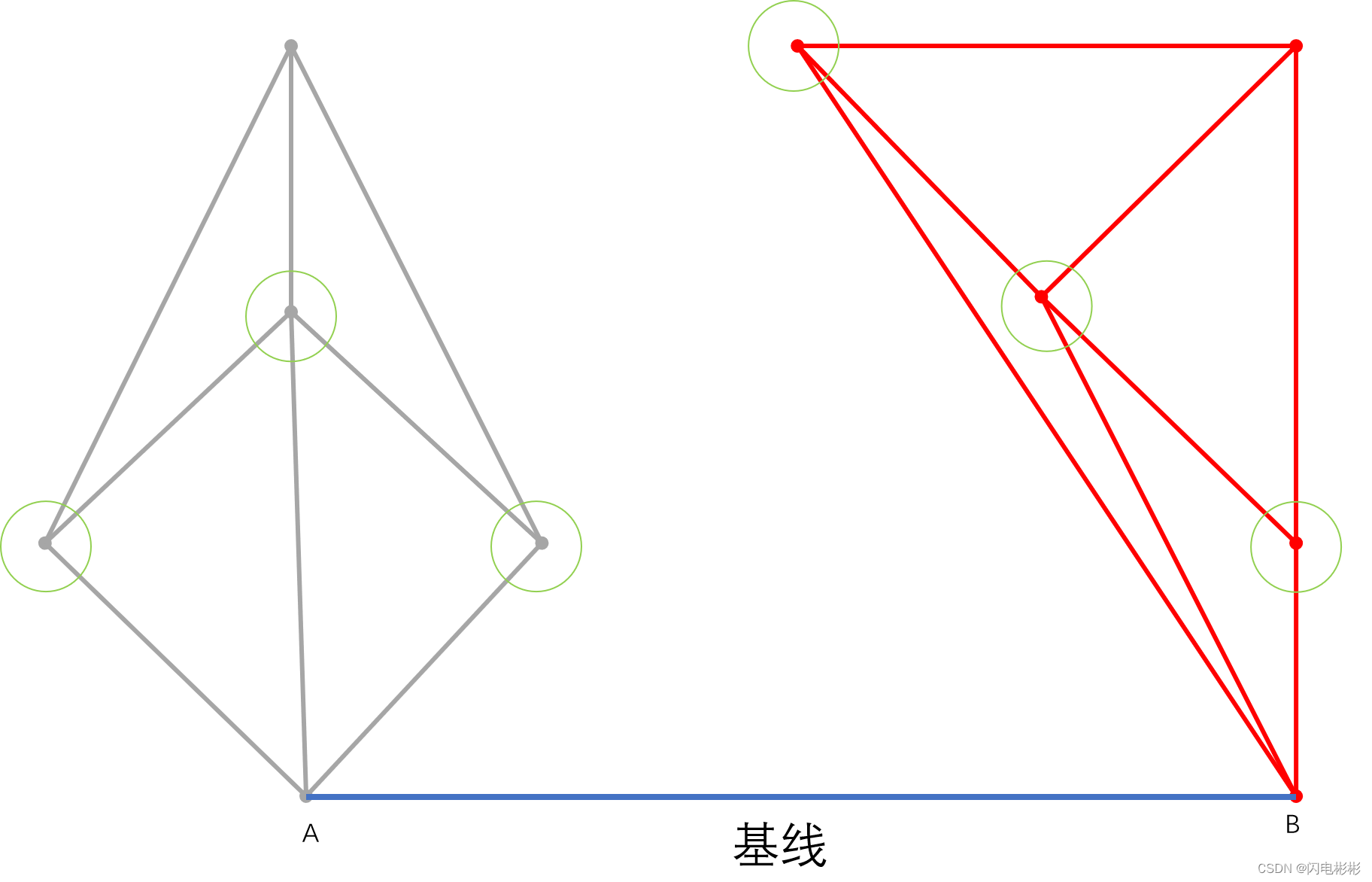
绿色圈中的点都为候选点，它们与A,B有边，且边与基线夹角小180度。

3 选中点，添加新边，更新基线
选中1个点p，使得pab所在外接圆不包含任何其他候选点。
具体算法在实现细节中给出。

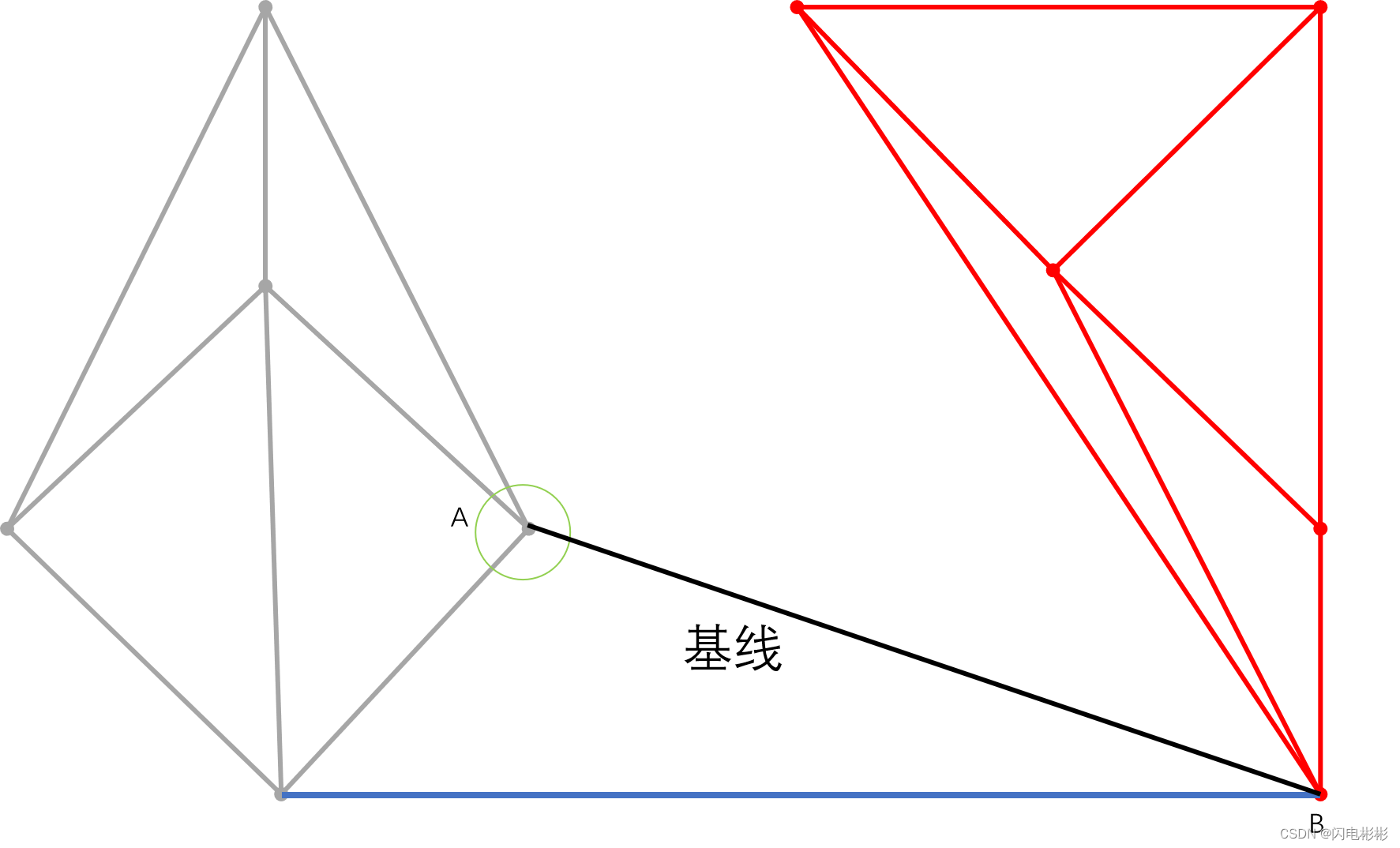
经过测试绿圆中的点为选中点, 添加边，更新基线位置。

到此，一次子操作就完成了。

继续上面步骤，依次添加和消失的边如下

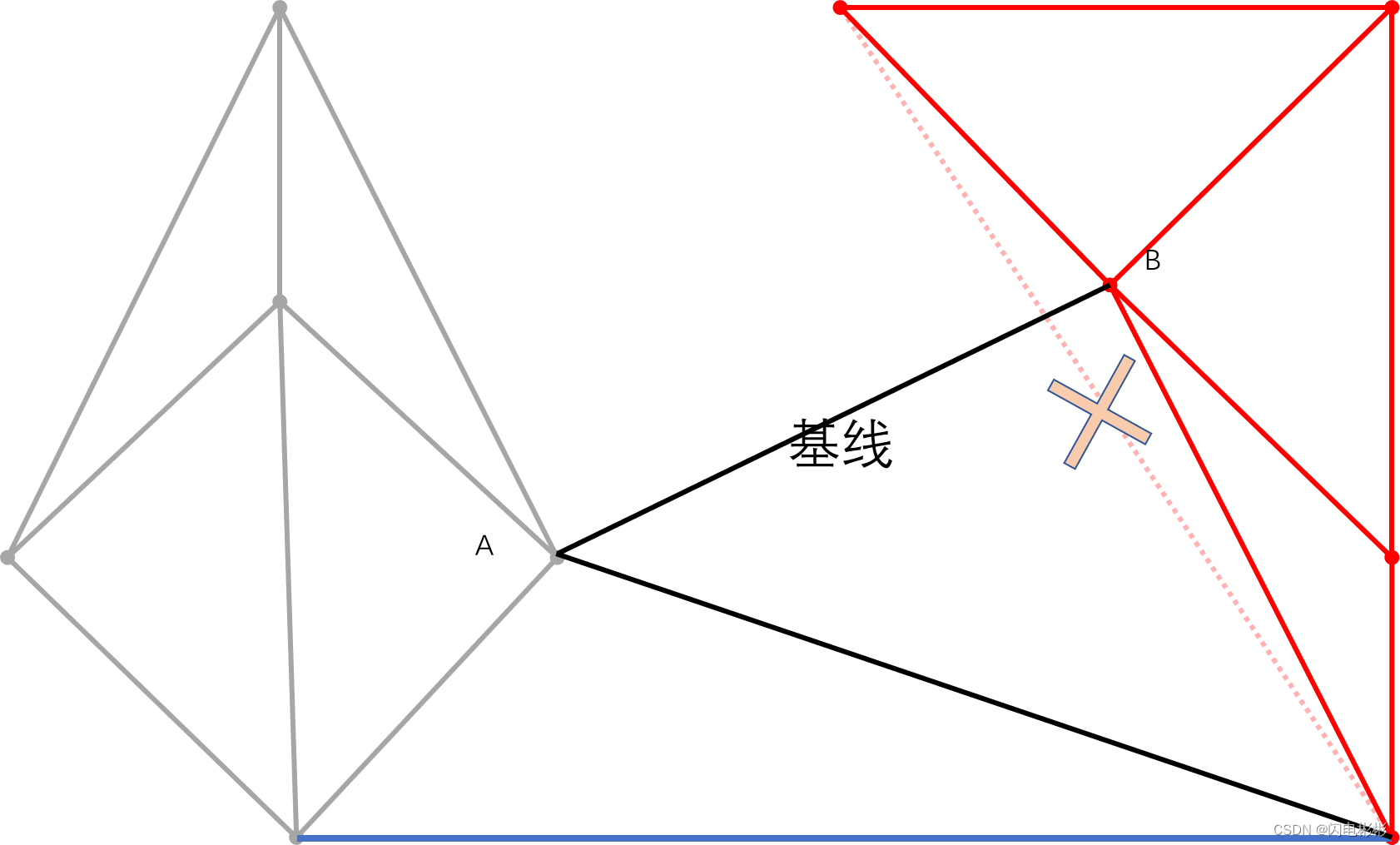
新的边与虚线有相交，需要删除。

继续加边

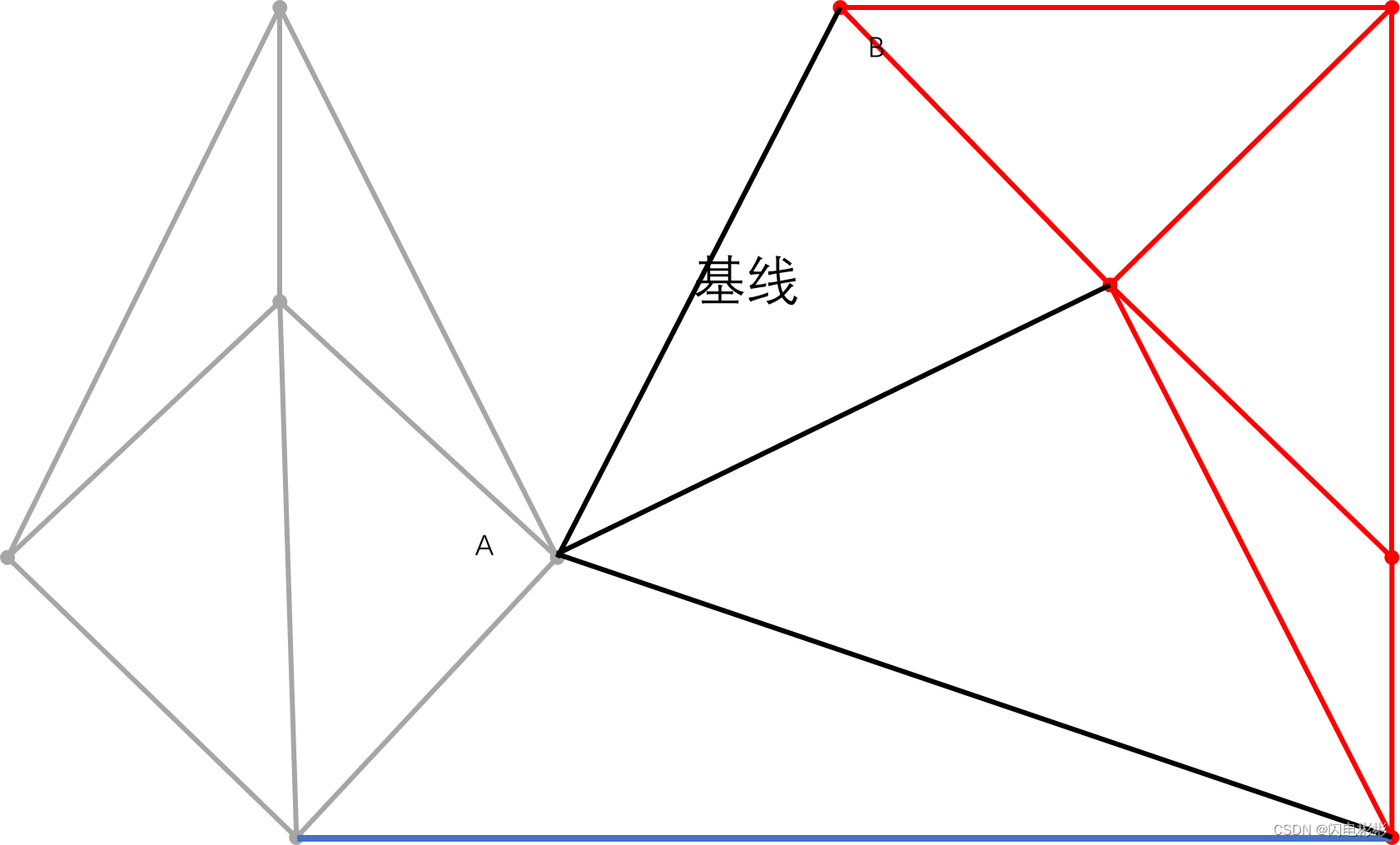
继续加边

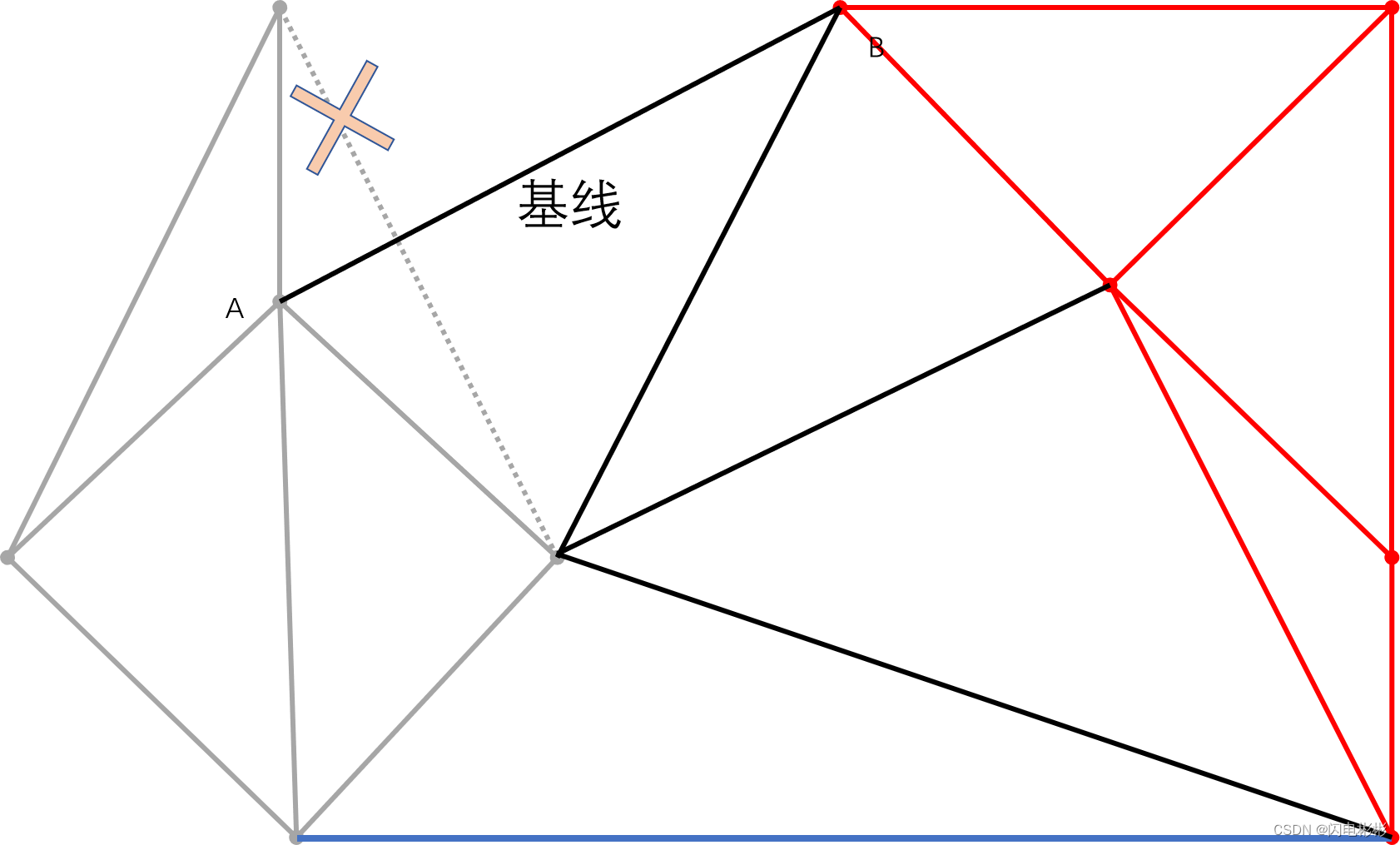
同样新边与现有边相交需要删除。

再添加新的边

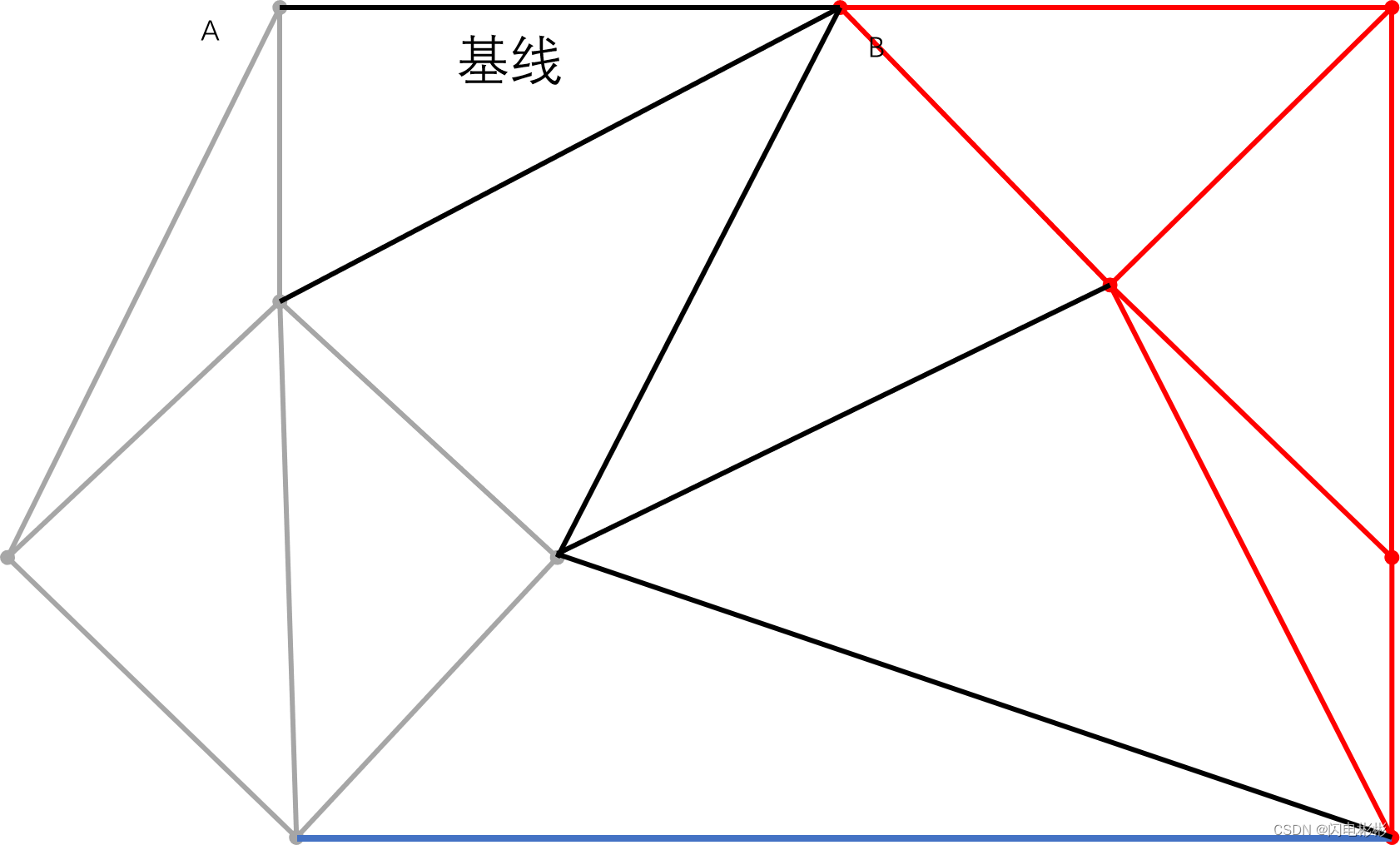
到此没有候选点在基线左上方。合并步骤结束。

实现细节

查找基线算法

由于点进行了排序，对于两个待合并的点集Q1（左边），Q2（右边）。
Q2的所有点肯定是在Q1的所有点的右上方。

已知Q1, Q2的外壳是一个凸包，所以基线的另一个性质是Q1,Q2中所有点都在基线的左上方。

具体实现思路：

1. 选择Q1中的任意点为基线的左点，选择Q2中的任意点为基线的右点。
2. 依次遍历Q1中的点，如果不在基线的左上方，则把左点更新，如果重合则选择长度短的，直到左点不更新。
3. 依次遍历Q2中的点，如果不在基线的左上方，则把右点更新，如果重合则选择长度短的，直到右点不更新，继续步骤2。

上述算法复杂度是O(n^2)

遍历优化：
在优化过程中，基线的点是不断往右下方移，之前遍历过的点是不需要再重复遍历。
所以，在遍历时可以根据当点的邻接点来遍历，不需要全部。
这样每个点最多被遍历一次，算法复杂度在O(n)。

如何从候选点找到选中点

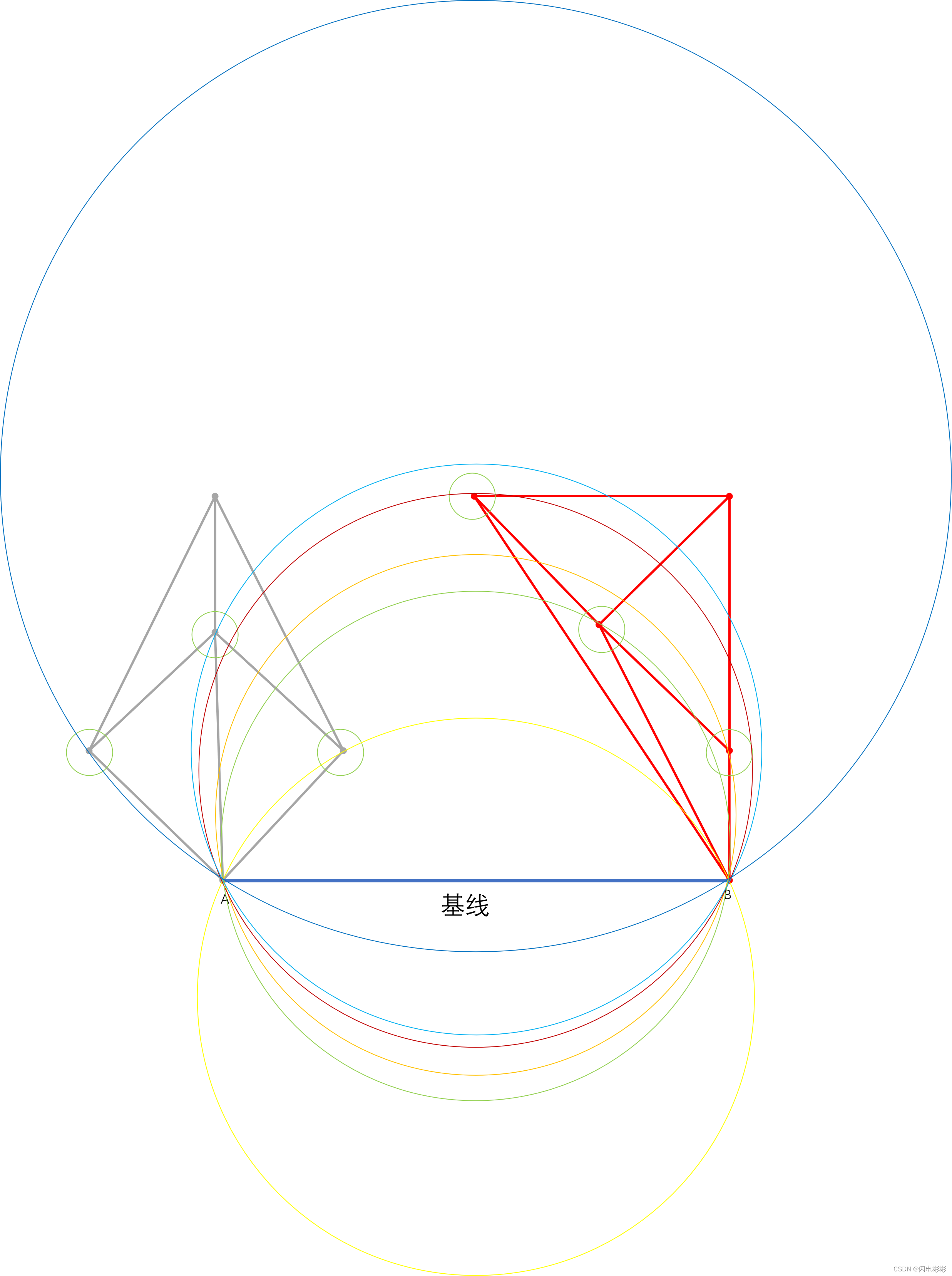
枚举出所有点形成的圆，可以看出只有基线往上面积最小的圆是符合要求的。

算法过程：
随机选中1点为选中点，遍历剩下的点，如果当前遍历点在外接圆里面，则更新当前遍历点为选中点。

删除边实现

1. 相交判断参考往期文章，利用跨立测试进行判断。 点击前往
2. 对边删除实现
   使用双边数据结构，在每一条边结构里加入一个对边指针。
   在删除自身时可以直接删除对边。

判断空圆性

利用三维抛物面判断点击前往

内存占用

主要是边数量的估计，点击前往

疑惑：新加入的边会之前构建三角形的空圆性

这里有一个疑惑需要解决。

在算法中每次检测空圆性只关注基线以上的点，有没有可能在加入新的边后影响到基线以下三角形的空圆性，如下图。

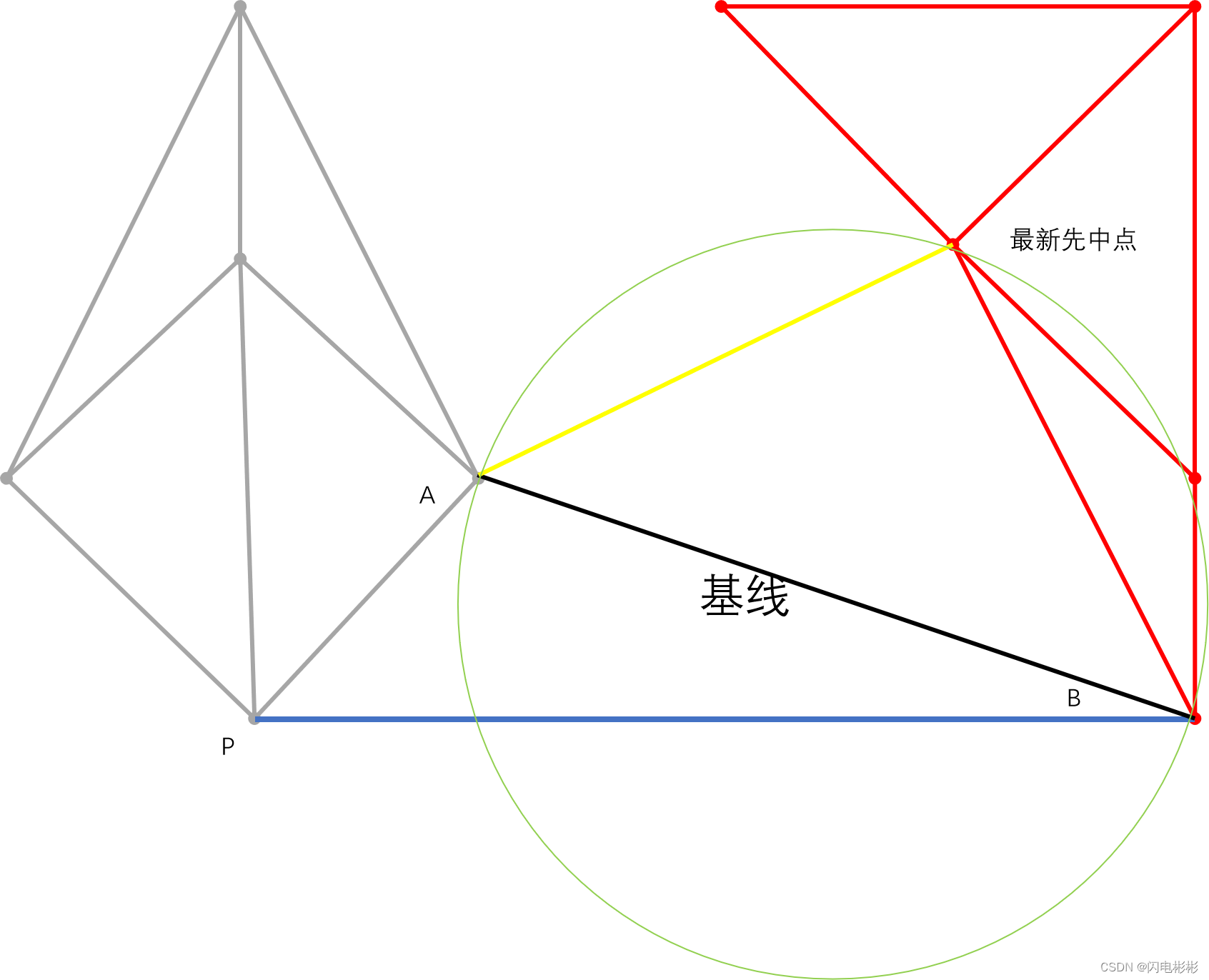
绿色圆有可能包含P点。

答案是不能。

先证明一个引理

引理1：如果一个4边形4点共圆，那么对角相加为180度

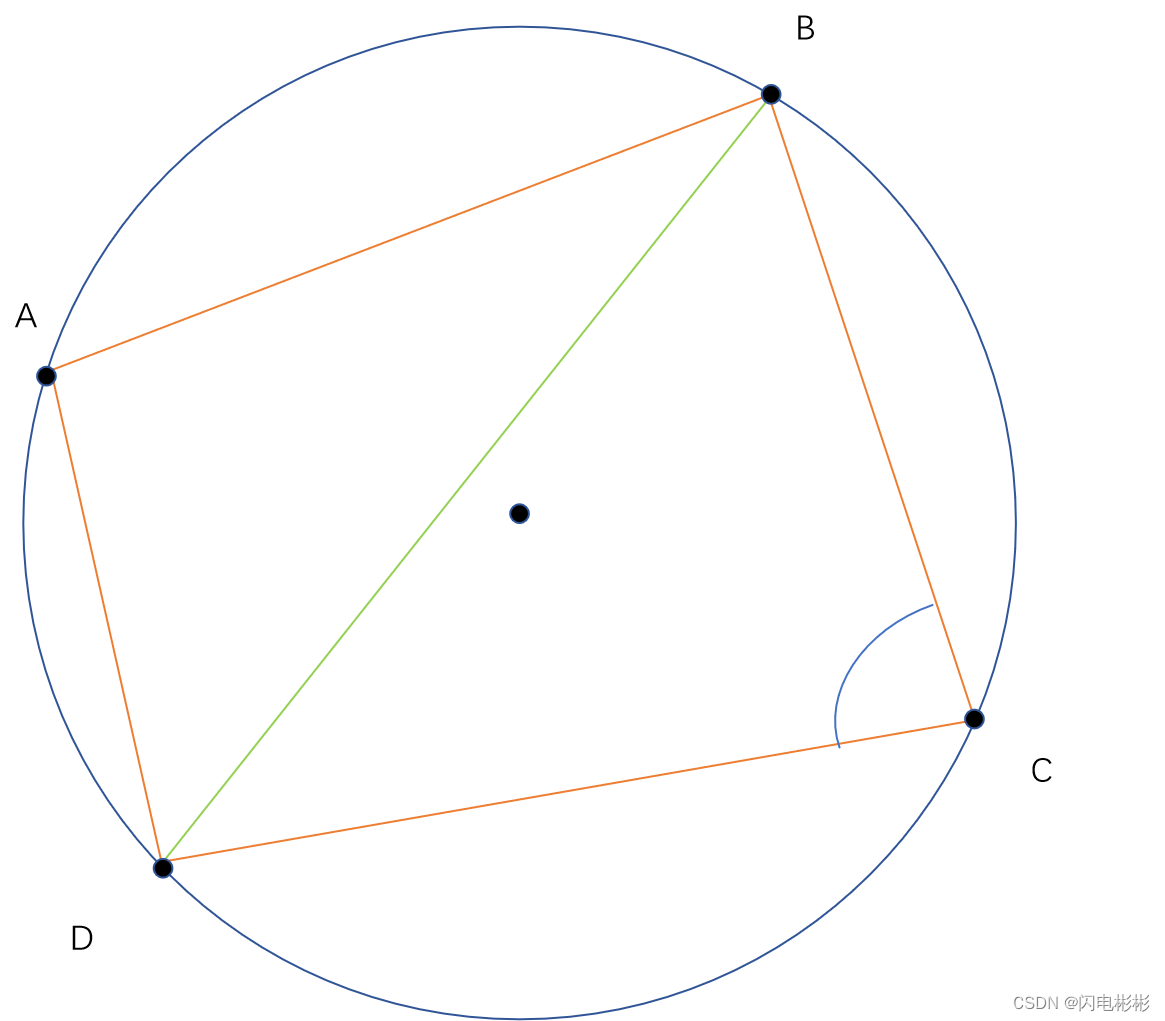
如上图，A,B,C,D 4点共圆。
$则\angle C+\angle A=180$

证明：

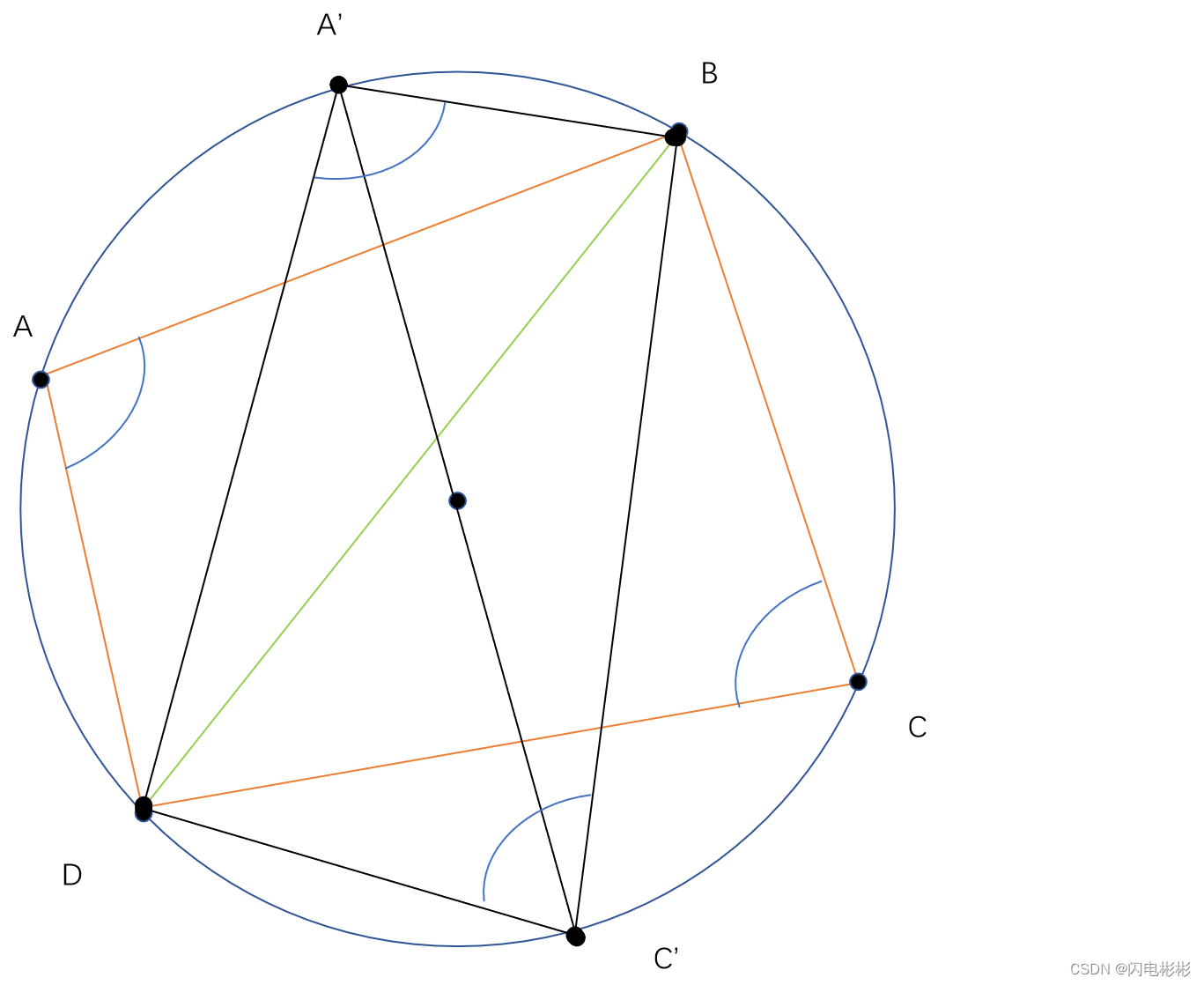
过圆心作一个直径A’C’, 连接A’D, A’B, C’D, C’B.

$可知\angle A^{\prime }D{C}^{\prime }=\angle C^{\prime }B{A}^{\prime }=90^0$

$根据四边形内角和为360^0,可知\angle B{C}^{\prime }D+\angle B{A}^{\prime }D=180^0$

$又\because \angle A和\angle D{A}^{\prime }B为同弦同侧圆周角，\angle C和\angle D{C}^{\prime }B为同弦同侧圆周角$

$\therefore \angle A=\angle D{A}^{\prime }B，\angle C=\angle D{C}^{\prime }B$

$\therefore \angle A+\angle C=\angle D{C}^{\prime }B+\angle D{A}^{\prime }B=180^0$

命题得证

引理2：4边形中如果1点所在角与对角和与180关系判断该点与另3点外接圆的关系

根据引理1可以得到如下结论：

4边形中如果1点所在角与对角和

1） >180: 在另三点外接圆内。
2）=180：在另三点外接圆上。
3）<180：在另三点外接圆外。

上述关系逆命题也成立。

之后加入的边不会影响之前的空圆性

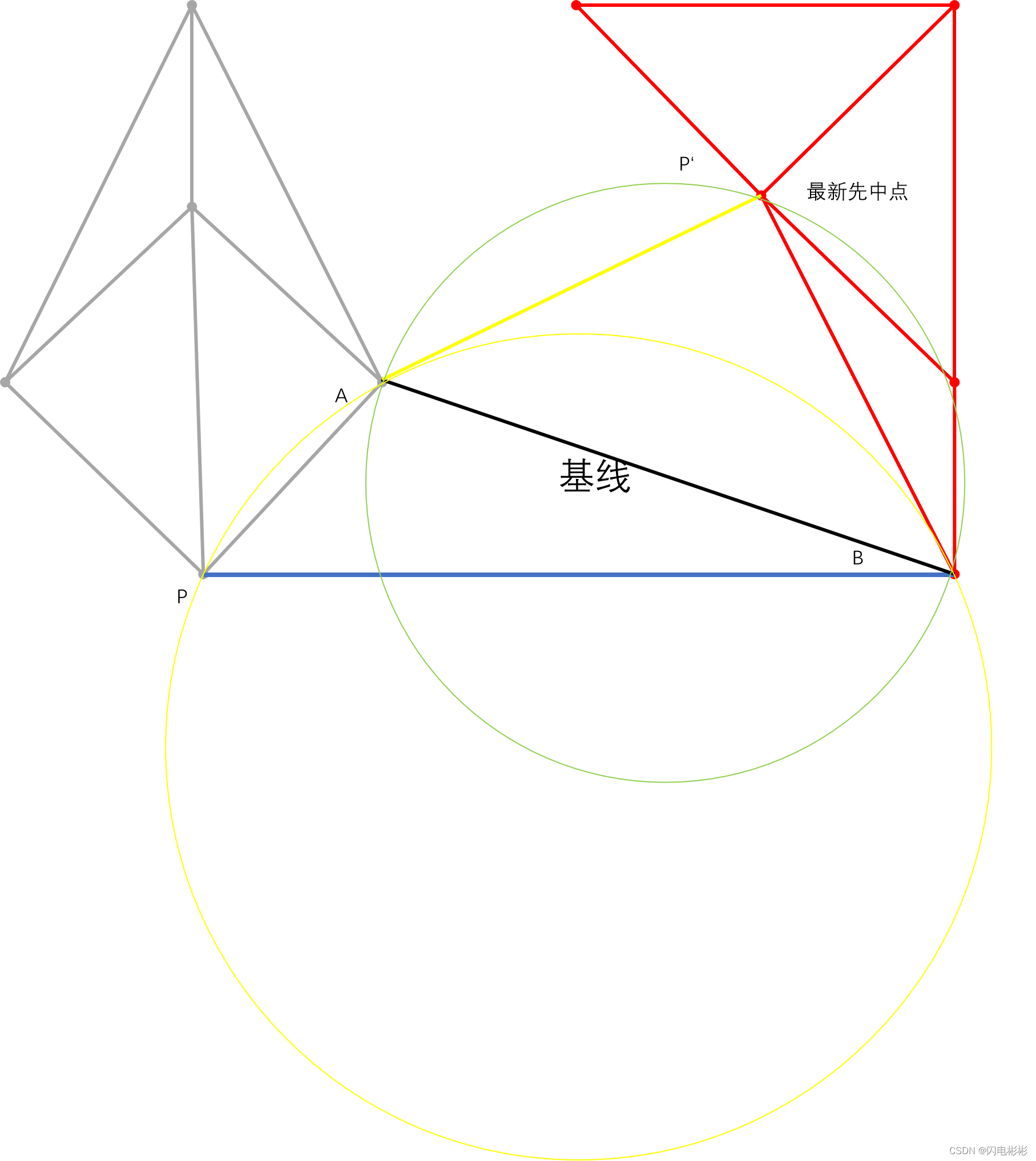
如上图，根据定义黄色的圆不会包含任何点

$可知，点p^{\prime }是在圆外面，\angle APB+\angle B{P}^{\prime }A<180^0$

$所以，反过来绿色的圆也不会包含P点$

代码模板

class Delaunay {
public:std::list<EdgeDelaunay> head[N];  // graphPoint p[N];int n=0;void init(int psize, Point ps[]) {this->n = psize;memcpy(this->p, ps, sizeof(Point) * n);std::sort(this->p, this->p + n);divide(0, n - 1);}void addEdge(int u, int v) {head[u].push_front(EdgeDelaunay(v));head[v].push_front(EdgeDelaunay(u));head[u].begin()->c = head[v].begin();head[v].begin()->c = head[u].begin();}void divide(int l, int r) {if (r - l <= 1) {  // #point <= 2for (int i = l; i <= r; i++)for (int j = i + 1; j <= r; j++) addEdge(i, j);return;}int mid = (l + r) / 2;divide(l, mid);divide(mid + 1, r);std::list<EdgeDelaunay>::iterator it;int nowl = l, nowr = r;for (int update = 1; update;) {// 查找左边最低线位置update = 0;Point ptL = p[nowl], ptR = p[nowr];for (it = head[nowl].begin(); it != head[nowl].end(); it++) {Point t = p[it->id];double v = cross(ptL - ptR, t - ptR);if (cmp(v) > 0 || (cmp(v) == 0 && (t - ptR).dis() < (ptL - ptR).dis())) {nowl = it->id, update = 1;break;}}if (update) continue;// 查找右边最低线位置for (it = head[nowr].begin(); it != head[nowr].end(); it++) {Point t = p[it->id];double v = cross(ptR - ptL, t - ptL);if (cmp(v) < 0 || (cmp(v) == 0 && (t - ptL).dis() < (ptL - ptR).dis())) {nowr = it->id, update = 1;break;}}}addEdge(nowl, nowr);  // 添加基线for (; true;) {Point ptL = p[nowl], ptR = p[nowr];int ch = -1, side = 0;for (it = head[nowl].begin(); it != head[nowl].end(); it++) {if (cmp(cross(ptR - ptL, p[it->id] - ptL)) <= 0)continue; // 判断夹角是否小于180if (ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0) {ch = it->id, side = -1;}}for (it = head[nowr].begin(); it != head[nowr].end(); it++) {if (cmp(cross(p[it->id] - ptR, ptL - ptR)) <= 0) continue;// 判断夹角是否小于180if (ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0) {ch = it->id, side = 1;}}if (ch == -1) break;  // 所有线已经加完if (side == -1) {for (it = head[nowl].begin(); it != head[nowl].end();) {// 判断是否相交，边缘不算相交if (cross(Line(ptL, p[it->id]), Line(ptR, p[ch]))) {head[it->id].erase(it->c);head[nowl].erase(it++);}else {it++;}}nowl = ch;addEdge(nowl, nowr);}else {for (it = head[nowr].begin(); it != head[nowr].end();) {// 判断是否相交，边缘不算相交if (cross(Line(ptR, p[it->id]), Line(ptL, p[ch]))) {head[it->id].erase(it->c);head[nowr].erase(it++);}else {it++;}}nowr = ch;addEdge(nowl, nowr);}}}std::vector<std::pair<int, int> > getEdge() {std::vector<std::pair<int, int> > ret;ret.reserve(n);std::list<EdgeDelaunay>::iterator it;for (int i = 0; i < n; i++) {//printf("%d : ", p[i].id);for (it = head[i].begin(); it != head[i].end(); it++) {//printf("%d, ", p[it->id].id);if (it->id < i) continue;ret.push_back(std::make_pair(p[i].id, p[it->id].id));}//puts("");}return ret;}
};

练习一

题目链接：https://codeforces.com/problemsets/acmsguru/problem/99999/383

题目大意

沙漠中有很多绿洲用点表示。有很多支队伍，每支队都有自己的起点和终点，队伍在行进过程中都要经过很多绿洲休息，所以都希望从一个绿洲出发时尽快的到下一个绿洲（也就是希望经过两个绿洲越近越好）。

也就是希望经过所有绿洲中相邻两个绿洲距离最大值越小越好。

答案是求一支队伍在从起点到终点经过的绿洲中最远的2个绿洲距离。

思路分析

首先题目只给出点，没有给出点与点之间的通路。

那么首先就要确定1个点到周围哪些点需要有通路。这个可以通过delaunay三角化解决。

有很了边以后，需要去掉很多没有用的边，肯定是希望边距离越小越好，可以使用最小生树，只留下必要的边。最小生成树点击前往

最后求2点之最经过的最大边，使用最近公共祖先解决点击前往

代码

#include<stdio.h>
#include<cmath>
#include <algorithm>
#include <vector>
#include <list>
#include <cstring>
#include <utility>using namespace std;
const double EPS = 1e-8;const int N = 1e5 + 10;
const int M = 1e5 + 10;int cmp(double d) {if (abs(d) < EPS)return 0;if (d > 0)return 1;return -1;
}class Point {
public:double x, y;int id;Point() {}Point(double a, double b) :x(a), y(b) {}Point(const Point& p) :x(p.x), y(p.y), id(p.id) {}void in() {scanf("%lf %lf", &x, &y);}void out() {printf("%f %f\n", x, y);}double dis() {return sqrt(x * x + y * y);}double dis2() {return x * x + y * y;}Point operator -() const {return Point(-x, -y);}Point operator -(const Point& p) const {return Point(x - p.x, y - p.y);}Point operator +(const Point& p) const {return Point(x + p.x, y + p.y);}Point operator *(double d)const {return Point(x * d, y * d);}Point operator /(double d)const {return Point(x / d, y / d);}void operator -=(Point& p) {x -= p.x;y -= p.y;}void operator +=(Point& p) {x += p.x;y += p.y;}void operator *=(double d) {x *= d;y *= d;}void operator /=(double d) {this ->operator*= (1 / d);}bool operator<(const Point& a) const {return x < a.x || (abs(x - a.x) < EPS && y < a.y);}bool operator==(const Point& a) const {return abs(x - a.x) < EPS && abs(y - a.y) < EPS;}
};// 向量操作double cross(const Point& a, const Point& b) {return a.x * b.y - a.y * b.x;
}double dot(const Point& a, const Point& b) {return a.x * b.x + a.y * b.y;
}class Point3D {
public:double x, y, z;Point3D() {}Point3D(double a, double b, double c) :x(a), y(b), z(c) {}Point3D(const Point3D& p) :x(p.x), y(p.y), z(p.z) {}double dis() {return sqrt(x * x + y * y + z * z);}double dis2() {return x * x + y * y + z * z;}Point3D operator -(const Point3D& p) const {return Point3D(x - p.x, y - p.y, z - p.z);}Point3D operator +(const Point3D& p) const {return Point3D(x + p.x, y + p.y, z + p.z);}Point3D operator *(double d)const {return Point3D(x * d, y * d, z * d);}Point3D operator /(double d)const {return Point3D(x / d, y / d, z / d);}void operator -=(Point3D& p) {x -= p.x;y -= p.y;z -= p.z;}void operator +=(Point3D& p) {x += p.x;y += p.y;z += p.z;}void operator *=(double d) {x *= d;y *= d;z *= d;}void operator /=(double d) {this ->operator*= (1 / d);}
};// 向量操作
Point3D cross(const Point3D& a, const Point3D& b) {return Point3D(a.y * b.z - a.z * b.y, -a.x * b.z + a.z * b.x,a.x * b.y - a.y * b.x);
}double dot(const Point3D& a, const Point3D& b) {return a.x * b.x + a.y * b.y + a.z * b.z;
}class Line {
public:Point front, tail;Line() {}Line(Point a, Point b) :front(a), tail(b) {}
};/*
0 不相交
1 相交
0 平行/重合
*/
int cross(const Line& a, const Line& b) {Point dir1 = a.front - a.tail;Point dir2 = b.front - b.tail;if (cmp(cross(dir1, dir2)) == 0) {return 0;}if (cmp(cross(a.front - b.tail, dir2)) * cmp(cross(a.tail - b.tail, dir2)) >= 0)return 0;if (cmp(cross(b.front - a.tail, dir1)) * cmp(cross(b.tail - a.tail, dir1)) >= 0)return 0;return 1;
}int inCircle(Point p0, Point p1, Point p2, Point p3) {Point d1 = p1 - p0;Point d2 = p2 - p0;if (cross(d1, d2) < 0)return inCircle(p0, p2, p1, p3); // 保证平面法向向上// 构建映射点Point3D lift0(p0.x, p0.y, p0.dis2());Point3D lift1(p1.x, p1.y, p1.dis2());Point3D lift2(p2.x, p2.y, p2.dis2());Point3D lift3(p3.x, p3.y, p3.dis2());Point3D z1(lift1 - lift0), z2(lift2 - lift0);Point3D normal = cross(z1, z2); // 计算平面法向double project = dot(normal, lift3 - lift0); // 计算点到平面距离return cmp(project);
}// https://oi-wiki.org//geometry/inverse/#%E5%8F%82%E8%80%83%E8%B5%84%E6%96%99%E4%B8%8E%E6%8B%93%E5%B1%95%E9%98%85%E8%AF%BB
// 根据官方定义实现圆的反演
class Circle
{
public:Point center;double r;Circle(const Point& c, double a) :center(c), r(a) {}Circle() {}void in() {center.in();scanf("%lf", &r);}void out() {center.out();printf("%f\n", r);}// 不过圆心的圆进行反演，得到1个圆Circle invert(const Circle& A) {Circle B;double oa = (center - A.center).dis();B.r = r * r / 2 * (1.0 / (oa - A.r) - 1.0 / (oa + A.r));double ob = r * r / (oa + A.r) + B.r;B.center = center + (A.center - center) * ob / oa;return B;}// 过圆心的圆进行反演，得到1条直线Point invert2line(const Circle& c) {return Point();}// 求反演点Point invertPoint(const Point& p) {Point dir = p - center;double dis = dir.dis();dir /= dis;dis = r * r / dis;return center + dir * dis;}// 直线反演，得到圆Circle invert2circle(const Line& l) {Point dir = l.front - l.tail;dir /= dir.dis();Circle c(Point(0, 0), 0);// 计算投影Point cdir = center - l.tail;Point project = l.tail + dir * (dir.x * cdir.x + dir.y * cdir.y);// 点乘得到投影长度// 计算圆到直线的距离Point op = project - center;if (op.dis() < 1e-6)return c;// 直线与圆心重合非法// 求解圆上的最远点double d = r * r / op.dis();Point pf = center + op / op.dis() * d;c.center = (center + pf) / 2;c.r = d / 2;return c;}};class Edge {
public:Edge() {}Edge(int t, int n, double w) :to(t), next(n), weight(w) {}int index;int from;int to;int next;double weight;bool isValid() const { return to >= 0; }
};class EdgeDelaunay {
public:int id;std::list<EdgeDelaunay>::iterator c;EdgeDelaunay(int id = 0) { this->id = id; }
};class Delaunay {
public:std::list<EdgeDelaunay> head[N];  // graphPoint p[N];int n=0;void init(int psize, Point ps[]) {this->n = psize;memcpy(this->p, ps, sizeof(Point) * n);std::sort(this->p, this->p + n);divide(0, n - 1);}void addEdge(int u, int v) {head[u].push_front(EdgeDelaunay(v));head[v].push_front(EdgeDelaunay(u));head[u].begin()->c = head[v].begin();head[v].begin()->c = head[u].begin();}void divide(int l, int r) {if (r - l <= 1) {  // #point <= 2for (int i = l; i <= r; i++)for (int j = i + 1; j <= r; j++) addEdge(i, j);return;}int mid = (l + r) / 2;divide(l, mid);divide(mid + 1, r);std::list<EdgeDelaunay>::iterator it;int nowl = l, nowr = r;for (int update = 1; update;) {// 查找左边最低线位置update = 0;Point ptL = p[nowl], ptR = p[nowr];for (it = head[nowl].begin(); it != head[nowl].end(); it++) {Point t = p[it->id];double v = cross(ptL - ptR, t - ptR);if (cmp(v) > 0 || (cmp(v) == 0 && (t - ptR).dis() < (ptL - ptR).dis())) {nowl = it->id, update = 1;break;}}if (update) continue;// 查找右边最低线位置for (it = head[nowr].begin(); it != head[nowr].end(); it++) {Point t = p[it->id];double v = cross(ptR - ptL, t - ptL);if (cmp(v) < 0 || (cmp(v) == 0 && (t - ptL).dis() < (ptL - ptR).dis())) {nowr = it->id, update = 1;break;}}}addEdge(nowl, nowr);  // 添加基线for (; true;) {Point ptL = p[nowl], ptR = p[nowr];int ch = -1, side = 0;for (it = head[nowl].begin(); it != head[nowl].end(); it++) {if (cmp(cross(ptR - ptL, p[it->id] - ptL)) <= 0)continue; // 判断夹角是否小于180if (ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0) {ch = it->id, side = -1;}}for (it = head[nowr].begin(); it != head[nowr].end(); it++) {if (cmp(cross(p[it->id] - ptR, ptL - ptR)) <= 0) continue;// 判断夹角是否小于180if (ch == -1 || inCircle(ptL, ptR, p[ch], p[it->id]) < 0) {ch = it->id, side = 1;}}if (ch == -1) break;  // 所有线已经加完if (side == -1) {for (it = head[nowl].begin(); it != head[nowl].end();) {// 判断是否相交，边缘不算相交if (cross(Line(ptL, p[it->id]), Line(ptR, p[ch]))) {head[it->id].erase(it->c);head[nowl].erase(it++);}else {it++;}}nowl = ch;addEdge(nowl, nowr);}else {for (it = head[nowr].begin(); it != head[nowr].end();) {// 判断是否相交，边缘不算相交if (cross(Line(ptR, p[it->id]), Line(ptL, p[ch]))) {head[it->id].erase(it->c);head[nowr].erase(it++);}else {it++;}}nowr = ch;addEdge(nowl, nowr);}}}std::vector<std::pair<int, int> > getEdge() {std::vector<std::pair<int, int> > ret;ret.reserve(n);std::list<EdgeDelaunay>::iterator it;for (int i = 0; i < n; i++) {//printf("%d : ", p[i].id);for (it = head[i].begin(); it != head[i].end(); it++) {//printf("%d, ", p[it->id].id);if (it->id < i) continue;ret.push_back(std::make_pair(p[i].id, p[it->id].id));}//puts("");}return ret;}
};class Graph {
public:int size;Graph() {}void init(int n) {size = n;head.assign(n, -1);edge.resize(M * 4);len = 0;emptyEdge = Edge(-1, -1, 0);}Edge headEdge(int a) {if (head[a] < 0)return emptyEdge;return edge[head[a]];}Edge nextEdge(const Edge& ed) {if (ed.next < 0)return emptyEdge;return edge[ed.next];}void add(int a, int b, double w) {//printf("add : %d %d %.6lf\n", a, b, w);edge[len] = Edge(b, head[a], w);edge[len].index = len;head[a] = len;len++;}private:vector<int> head;int len;Edge emptyEdge;vector<Edge> edge;
};Graph g;class UnionFindSet {
private:vector<int> father; // 父结点定义，father[i]=i时，i为本集合的代表vector<int> height; // 代表树高度，初始为1int nodeNum; // 集合中的点数public:UnionFindSet(int n); // 初始化bool Union(int x, int y); // 合并int Find(int x);bool UnionV2(int x, int y); // 合并int FindV2(int x);
};UnionFindSet::UnionFindSet(int n) : nodeNum(n + 1) {father = vector<int>(nodeNum);height = vector<int>(nodeNum);for (int i = 0; i < nodeNum; ++i) father[i] = i, height[i] = 1; // 初始为自己
}int UnionFindSet::Find(int x) {while (father[x] != x) x = father[x];return x;
}bool UnionFindSet::Union(int x, int y) {x = Find(x);y = Find(y);if (x == y)return false;father[x] = y;return true;
}int UnionFindSet::FindV2(int x) {int root = x; // 保存好路径上的头结点while (father[root] != root) {root = father[root];}/*从头结点开始一直往根上遍历把所有结点的father直接指向root。*/while (father[x] != x) {// 一定要先保存好下一个结点，下一步是要对father[x]进行赋值int temp = father[x];father[x] = root;x = temp;}return root;
}/*
需要加入height[]属性，初始化为1.
*/
//合并结点
bool UnionFindSet::UnionV2(int x, int y) {x = Find(x);y = Find(y);if (x == y) {return false;}if (height[x] < height[y]) {father[x] = y;}else if (height[x] > height[y]) {father[y] = x;}else {father[x] = y;height[y]++;}return true;
}// 最小生成树
class MST {vector<Edge> edges;UnionFindSet ufs;public:MST(int n, vector<Edge>& ed) :ufs(n), edges(ed) { g.init(n); }void build() {sort(edges.begin(), edges.end(), [=](Edge& a, Edge& b)->bool {return a.weight < b.weight; });for (auto d : edges) {if (ufs.UnionV2(d.from, d.to)) {g.add(d.from, d.to, d.weight);g.add(d.to, d.from, d.weight);}}}
};const int bitL = 22;
class LCA {int h[N];int father[bitL][N];double dis[bitL][N];
public:void dfs(int x, int fa, double w){if (fa == -1) h[x] = 0;else {h[x] = h[fa] + 1;father[0][x] = fa;dis[0][x] = w;for (int t = 1; t < bitL && (1 << t) <= h[x]; t++) {father[t][x] = father[t - 1][father[t - 1][x]];dis[t][x] = max(dis[t - 1][x], dis[t - 1][father[t - 1][x]]);}}for (auto ed = g.headEdge(x); ed.isValid(); ed = g.nextEdge(ed)){int j = ed.to;if (fa == j)continue;dfs(j, x, ed.weight);}}int lca(int a, int b) {if (h[a] < h[b]) {return lca(b, a);}int gap = h[a] - h[b];for (int t = bitL - 1; t >= 0; t--) {if (gap & (1 << t))a = father[t][a];}if (a == b)return a;gap = h[a];for (int t = bitL - 1; t >= 0; t--) {if (gap <= (1 << t))continue;if (father[t][a] == father[t][b])continue;a = father[t][a];b = father[t][b];gap -= 1 << t;}return father[0][a];}double optDis(int a, int b) {if (h[a] < h[b]) {return optDis(b, a);}double d = 0;int gap = h[a] - h[b];for (int t = bitL - 1; t >= 0; t--) {if (gap & (1 << t)) {d = max(d, dis[t][a]);a = father[t][a];}}if (a == b)return d;gap = h[a];for (int t = bitL - 1; t >= 0; t--) {if (gap <= (1 << t))continue;if (father[t][a] == father[t][b])continue;d = max(d, dis[t][a]);d = max(d, dis[t][b]);a = father[t][a];b = father[t][b];gap -= 1 << t;}d = max(d, max(dis[0][a], dis[0][b]));return d;}
};Point oiPs[N];
Delaunay de;
LCA lc;void  solve() {int n, m;scanf("%d", &n);int a, b;for (int i = 0; i < n; ++i) {scanf("%d%d", &a, &b);oiPs[i].x = a;oiPs[i].y = b;oiPs[i].id = i;}de.init(n, oiPs);auto oiedges = de.getEdge();vector<Edge> edges;for (auto oie : oiedges) {Edge ed(oie.second, -1, (oiPs[oie.first] - oiPs[oie.second]).dis());ed.from = oie.first;edges.push_back(ed);}MST mst(n, edges);mst.build();/*for (int i = 0; i < n; ++i) {printf("%d : ", i);for (Edge ed = g.headEdge(i); ed.isValid(); ed = g.nextEdge(ed)) {printf("%d ", ed.to);}puts("");}*/lc.dfs(0, -1, 0);scanf("%d", &m);while (m--) {scanf("%d%d", &a, &b);a--, b--;printf("%.11f\n", lc.optDis(a, b));}
}int main() {solve();return 0;}/*
3
0 0
50 10
150 0
3
1 2
1 3
2 34
0 1
1 0
1 1
0 04
1 2
2 3
4 1
1 34
0 0
0 1
1 0
1 14
1 2
2 3
4 1
1 36
0 0
0 1
0 2
0 3
0 4
0 54
1 2
2 3
4 1
1 36
1 0
5 0
0 0
2 0
3 0
4 04
1 2
2 3
4 1
1 310
0 0
1 1
1 2
2 1
2 3
2 9
3 2
4 6
7 9
9 810
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
10 17
0 0
1 1
1 2
2 1
2 3
2 9
3 21
1 210
1 2
2 1
1 1
9 8
7 9
2 3
4 6
2 9
0 0
3 210
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
10 1*//*10
1 2
1.00000000000
2 3
1.00000000000
3 4
4.24264068712
4 5
2.23606797750
5 6
4.24264068712
6 7
3.60555127546
7 8
3.60555127546
8 9
3.60555127546
9 10
1.41421356237
10 1
1.414213562374
1 2
1.00000000000
2 3
1.00000000000
4 1
1.00000000000
1 3
1.00000000000
*/

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。创作不易，帮忙点击公众号的链接。

这篇关于AK F.*ing leetcode 流浪计划之delaunay三角化的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---