P中值选址问题的整数规划求解-cplex

问题介绍

p-中值选址问题是一个常见的选址问题. 问题是给定I个需求结点和J个待选设施地点, 要求选择p个地点建立设施, 使得运输成本最低。

数学模型

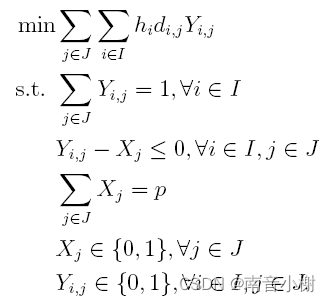
leapms介绍

使用Java+cplex求解问题前，先介绍一种全新且高效的建模工具——Leapms。
Leapms 是一个用于求解整数规划的免费建模语言，具备简洁的建模过程。Leapms 语言设计的原则包括：（1）采用描述性语言形式；（2）尽力与模型的数学表达形式一致。leapms软件应用网站：https://www.cnblogs.com/leapms/
语言开发者：陆教授(yplu@bjtu.edu.cn)

数据定义

//    数据参数定义
class DataMedian{//        需求double[] demand={3.1,2.2,4.3,5.0,7.1,8.0,9.9,3.4,4.3,3.3};//        距离矩阵double[][] distance={{73, 30, 15,  8, 67, 34, 82, 50,  9, 12},{89, 85, 90, 56, 79, 51, 52, 72, 51, 52},{26, 99, 60, 47, 47, 21, 20, 30, 42, 27},{97, 99, 89, 60, 96, 43,  2,  7, 45, 34},{27, 46, 34, 54, 61, 97, 12, 55, 39, 23},{73, 46, 81, 12, 15, 44, 46, 76, 48, 36},{6, 60, 31, 47, 41,  8, 34, 69, 57, 23},{46,  5, 45, 37, 14, 75, 72, 12, 15, 88},{42, 10, 93, 36, 19, 63, 71, 42, 94, 62},{62, 44, 66, 11, 88, 81, 52, 42, 81, 43}};//        选址数量int medianNumber=6;//        节点数量int nodeNumber=10;
}

问题建模

public class PMedianDemo {//    定义数据DataMedian data;public PMedianDemo(DataMedian data){this.data=data;}//    定义cplex内部对象IloCplex model;//    定义变量public IloNumVar[] x;public IloNumVar[][] y;//    求解函数public void solve() throws IloException {if(model.solve()==false){
//            模型不可解System.out.println("模型不可解");return;}else{System.out.println("目标值："+model.getObjValue());System.out.println("=========选择变量===========");for(int i=0;i<data.nodeNumber;i++){if(model.getValue(x[i])!=0) {System.out.println("变量值x[" + (i + 1) + "]:" + model.getValue(x[i]));}}System.out.println("=========分配关系===========");for(int i=0;i<data.nodeNumber;i++){for(int j=0;j<data.nodeNumber;j++) {if (model.getValue(y[i][j]) != 0) {System.out.println("变量值y[" + (i + 1) + "]["+(j+1)+"]:" + model.getValue(y[i][j]));}}}}}//    根据数学模型建立求解模型public void BuildModel() throws IloException{
//        modelmodel = new IloCplex();model.setOut(null);
//        variablesx = new IloNumVar[data.nodeNumber];y = new IloNumVar[data.nodeNumber][data.nodeNumber];
//        定义cplex变量x和y的数据类型及取值范围for(int i=0;i<data.nodeNumber;i++){x[i]=model.numVar(0,1, IloNumVarType.Int,"x["+i+"]");}for(int i=0;i<data.nodeNumber;i++){for(int j=0;j<data.nodeNumber;j++) {y[i][j] = model.numVar(0, 1, IloNumVarType.Int, "y[" + i + "]["+j+"]");}}
//        设置目标函数IloNumExpr obj = model.numExpr();for(int i=0;i<data.nodeNumber;i++){for(int j=0;j<data.nodeNumber;j++) {double odjTem=data.demand[i]*data.distance[i][j];obj = model.sum(obj, model.prod(odjTem,y[i][j]));}}model.addMinimize(obj);
//        添加约束1for(int i=0;i<data.nodeNumber;i++) {IloNumExpr expr1 = model.numExpr();for(int j=0;j<data.nodeNumber;j++){expr1=model.sum(expr1,y[i][j]);}model.addEq(expr1,1);}
//        添加约束2for(int i=0;i<data.nodeNumber;i++) {for(int j=0;j<data.nodeNumber;j++){model.addLe(y[i][j],x[j]);}}
//        添加约束3IloNumExpr expr3 = model.numExpr();for(int j=0;j<data.nodeNumber;j++){expr3=model.sum(expr3,x[j]);}model.addEq(expr3,data.medianNumber);}

问题求解

public static void main(String[] args)throws IloException{DataMedian data =new DataMedian();PMedianDemo lp=new PMedianDemo(data);lp.BuildModel();lp.solve();}

求解结果

=======================================
今天到此为止，后续记录其他cplex技术的学习过程。
以上学习笔记，如有侵犯，请立即联系并删除！