Real-Time Rendering——9.8.2 Multiple-Bounce Surface Reflection多次反射表面反射

As mentioned earlier in Section 9.7, the microfacet BRDF framework does not account for light that is reflected (“bounced”) from the microsurface multiple times. This simplification causes some energy loss and over-darkening, especially for rough metals [712].

如之前在第9.7节中提到的，microfacet BRDF框架没有考虑从微表面多次反射(“反弹”)的光。这种简化导致一些能量损失和过度变暗，特别是对于粗糙金属[712]。

A technique used by Imageworks [947] combines elements from previous work [811, 878] to create a term that can be added to the BRDF to simulate multiple-bounce surface reflection:

Imageworks [947]使用的一项技术结合了之前工作[811，878]中的元素，创建了一个可以添加到BRDF中的项，以模拟多次反弹表面反射:

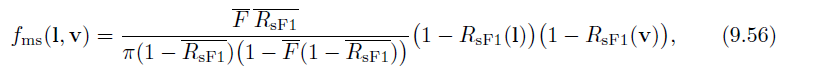
where RsF1 is the directional albedo (Section 9.3) of fsF1, which is the specular BRDF term with F0 set to 1. The function RsF1 depends on the roughness α and elevation angle θ. It is relatively smooth, so it can be precomputed numerically (using Equation 9.8 or 9.9) and stored in a small two-dimensional texture. Imageworks found that 32 × 32 resolution is sufficient. 

其中RsF1是fsF1的方向反照率(第9.3节)，fsF1是F0设置为1时的镜面BRDF项。函数RsF1取决于粗糙度α和仰角θ。它是相对平滑的，因此可以用数值方法预先计算(使用方程9.8或9.9)并存储在一个小的二维纹理中。Imageworks发现32 × 32的分辨率已经足够了。

The function RsF1 is the cosine-weighted average value of RsF1 over the hemisphere. It depends only on α, so it can be stored in a one-dimensional texture, or an inexpensive curve could be fitted to the data. Since RsF1 is rotationally symmetric about n, RsF1 can be computed with a one-dimensional integral. We also use the change of variables μ = cos θ (see Equation 9.6 on page 312):

函数RsF1是RsF1在整个半球上的余弦加权平均值。它只依赖于α，所以它可以存储在一维纹理中，或者可以用一条便宜的曲线来拟合数据。因为RsF1关于n旋转对称，所以RsF1可以用一维积分来计算。我们还使用变量μ = cos θ的变化(见312页的方程9.6):

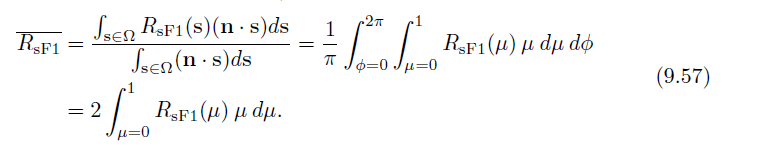
Finally, F is the cosine-weighted average of the Fresnel term, computed in the same way: 

最后，F是菲涅耳项的余弦加权平均值，计算方法相同:

Imageworks provide a closed-form solution to Equation 9.58 in the case that the generalized Schlick form (Equation 9.18) is used for F: 

Imageworks为方程9.58提供了一个封闭形式的解 施利克形式(方程9.18)用于F:

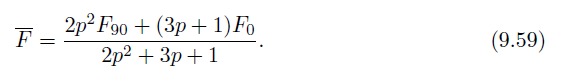
If the original Schlick approximation is used (Equation 9.16), then the solution simplifies to 

如果使用原始的施利克近似法(方程9.16)，则解简化为

In the case of anisotropy, Imageworks use an intermediate roughness between αx and αy for the purpose of computing fms. This approximation avoids the need to increase the dimensionality of the RsF1 lookup table, and the errors it introduces are small. 

在各向异性的情况下，Imageworks使用介于αx和αy之间的中间粗糙度来计算fms。这种近似避免了增加RsF1查找表维数的需要，并且它引入的误差很小。

The results of the Imageworks multiple-bounce specular term can be seen in Figure 9.39.

在图9.39中可以看到Imageworks多重反射镜面反射项的结果 .

Figure 9.39. In all rows the roughness of the surface increases from left to right. The top two rows show a gold material. The first row is rendered without the Imageworks multiple-bounce term, and the second is rendered with the multiple-bounce term. The difference is most noticeable for the rougher spheres. The next two rows show a black dielectric material. The third row is rendered without the multiple-bounce term, and the fourth row has the multiple-bounce term applied. Here the difference is more subtle, since the specular reflectance is much lower. (Figure courtesy of Christopher Kulla [947].) 

图9.39。在所有行中，表面的粗糙度从左到右增加。上面两行显示的是金色材质。第一行在不使用Imageworks多次反射术语的情况下进行渲染，第二行在使用多次反射术语的情况下进行渲染。对于较粗糙的球体，这种差异最为明显。接下来的两行显示黑色电介质材料。第三行渲染时没有多次反弹项，第四行应用了多次反弹项。这里的区别更加微妙，因为镜面反射率要低得多。(图由克里斯托弗·库拉[947]提供。)