混合模拟退火和教与学的鸽群优化算法-附代码

混合模拟退火和教与学的鸽群优化算法

摘要：为了改善鸽群优化算法（PIO）容易陷入局部最优和解精度较低的特点,提出一种混合模拟退火和教与学的鸽群优化算法。首先,将鸽群优化算法和模拟退火相结合,可以利用模拟退火跳出局部最优,得到较为精确的解。然后,在鸽群优化算法的速度更新公式中加入惯性权重,并采用线性递减的策略,与教与学算法相结合,增加种群的多样性。

1.鸽群算法

基础鸽群算法的具体原理参考，我的博客：https://blog.csdn.net/u011835903/article/details/109774886

2.改进鸽群优化算法

2.1 模拟退火鸽群优化算法

模拟退火 ${}^{[4]}$ 是模拟物体从高温降为低温的过程, 根据 Metropolis 准则, 由于降温操作, 物体从状态 $\mathrm{i}$ 变为状态 $\mathrm{j}$, 能 量也从 $E(i)$ 变为 $E(j)$, 能量的变化量为 $\Delta E=E(i)-E(j)$, 当 $\Delta E>0$, 接受变化的新状态; 当 $\Delta E<0$, 以一定的概率接 受当前的新状态。当概率 $p=\exp (E(i)-E(j)/T)>$ rand 时, 接受 当前的新状态, 否则保留旧的状态。其中, $\mathrm{T}=\mathrm{T}\cdot$ decayscale, decayscale 为退火系数。
模拟退火鸽群优化算法（SAPIO ) 是以鸽群优化算法为主 流程, 加人了模拟退火机制, 对每个鸽子的位置进行局部寻优, 使算法在接受较优解的同时, 以一定的概率接受较差解, 能够 使算法跳出局部最优。随着物体的降温, 能量逐渐趋于稳定状 态，算法达到全局最优。

2.2 线性递减的惯性权重和速度更新

在鸽群优化算法中, 前期需要较大的速度, 有利于全局搜 索, 能较快地定位最优解的大致位置。随着惯性权重的减小, 速度减小, 能够进行精细的局部搜索和得到更精确的解, 该方 法加快了算法的收敛速度, 提高了算法性能 ${}^{[5]}$ 。惯性权重的调 节和速度公式如下：
$$w=w_{\text{start }}-\frac{w_{\text{start }}-w_{\text{end }}}{T1}\times t\text{\hspace{1em}(6)}$$

$$\begin{array}{c}{v}_i^t=w\ast v_i^{t-1}\cdot e^{-Rt}+\mathrm{rand}\cdot \left(x_{\text{gbest }}-x_i^{t-1}\right)\end{array}\text{\hspace{1em}(7)}$$

2.3 教与学优化算法

教与学优化算法（TLBO） [6] 包括教师阶段和学习阶段。在教师阶段，选择种群中最好的个体作为教师，通过教行为提高学生的平均成绩。设 $x_{\text{teacher }}$ 是教师, $\alpha$ 是学习因子, 且 $\alpha =$ round $(1+$ rand $(0,1)),x_{\text{mean }}$ 种群内所有个体的平均值。教 师阶段的更新公式如下:
$$x_i^t=x_i^{t-1}+\mathrm{rand}(0,1)\times \left(x_{\text{teacher }}-\alpha \times x_{\text{mean }}\right)\text{\hspace{1em}(8)}$$
在学习阶段, 从种群中随机选出两个不同的个体 $x_p$ 和 $x_q$, 比较两个个体之间的差异。令 $x_i$ 向其中优秀的个体进行学习。 学生阶段的更新公式如下:
$$x_i^t=\{\begin{array}{ll}{x}_i^{t-1}+\mathrm{rand}(0,1)\times \left(x_p^t-x_i^{t-1}\right),& f\left(x_p\right)<f\left(x_q\right)\\ x_i^{t-1}+\mathrm{rand}(0,1)\times \left(x_q^t-x_i^{t-1}\right),& f\left(x_p\right)>f\left(x_q\right)\end{array}\text{\hspace{1em}(9)}$$
TLSAPIO 算法实现

输入: 种群规模 $\mathrm{N}$, 最大迭代次数 $\mathrm{T}1+\mathrm{T}2$ 。
输出：最优个体 $x_{\text{gbest 。 }}$
Step1: 初始化鸽群算法相关的参数, 包括速度和位置。
Step2: 计算鸽子的适应度值, 找出个体极值 $x_p$ 和全局极值 $x_{\text{gbest }\circ }$

Step3: 执行地图和指南针算子, 并根据公式（1）和（2） 更新鸽子的速度和位置。

Step4: 当 $t>\mathrm{T}1$ 时, 停止执行地图和指南针算子, 转而去执 行地标算子。否则继续 Step3。

Step5: 执行地标算子, 对鸽子的适应度值进行排序, 适应 度值较低的鸽子执行教与学优化算法, 并根据公式 (7) 、（8） 和（9）更新速度和位置, 同时计算适应度值。

Step6: 当 $t>\mathrm{T}2$ 时, 停止执行地标算子, 输出最后结果。否 则继续 Step5。

Step7: 计算两次位置变化引起的适应度值的变化量 $\Delta f=f_i\left(x_i(t+1)\right)-f_i\left(x_i(t)\right)$, 如果 $\Delta f<0$ 或 $\exp (-\Delta f/T)>$ rand, 则接受新位置, 否则保留旧位置。
Step8: 执行降温操作, $\mathrm{T}=\mathrm{T}\cdot$ decayscale。
Step9: 判断是否满足终止条件, 若满足, 则结束算法, 输 出全局最优值。否则转 Step2。

3.实验结果

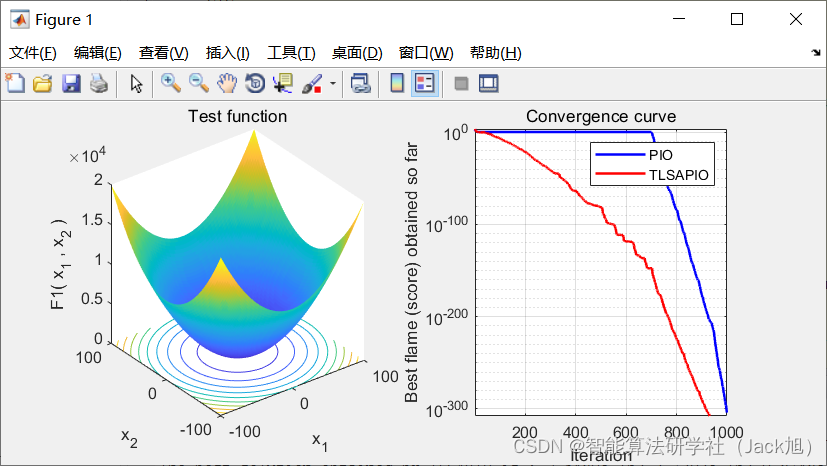
4.参考文献

[1]未建英,张丽娜,付发.混合模拟退火和教与学的鸽群优化算法[J].科技经济导刊,2019,27(12):153-155.

5.Matlab代码

6.python代码