本文主要是介绍多目标蜻蜓算法(MODA)附Matlab代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、MODA算法描述
二、MODA的伪代码
三、多目标蜻蜓算法(MODA)Matlab代码
四、运行结果
一、MODA算法描述
为了使用DA算法解决多目标问题,它首先配备了一个档案库(Archive),用于在优化过程中存储和检索最优解的最佳近似。搜索代理的更新位置与DA相同,但食物来源是从档案中选择的。类似于多目标粒子群优化算法,为了找到分布良好的帕累托最优前沿,从所获得的帕累托最优前沿的种群最少的区域中选择食物源。为了找到帕累托最优前沿的种群最少的区域,应该分割搜索空间。这是通过寻找得到的帕累托最优解的最佳和最差目标,定义一个超球来覆盖所有解,并在每次迭代中将超球划分为相等的子超球来实现的。在创建片段之后,通过轮盘赌机制进行选择,每个片段的概率如下,这是由Coello Coello等人提出的:
其中是大于1的常数,
是第i段中获得的帕累托最优解的个数。这个方程允许MODA算法有更高的概率从种群较少的部分选择食物来源。因此,将鼓励蜻蜓在这些区域周围飞行,并改善整个帕累托最优前沿的分布。然而,为了从档案库(Archive)中选择敌人,应该选择最差(种群最多)的超球体,以阻止蜻蜓在不太可能的拥挤区域搜索。选择是通过轮盘赌机制完成的,每个部分的概率如下:
其中是大于1的常数,
是第i段中获得的帕累托最优解的个数。在上式中可以看到。轮盘赌机制将高概率分配给最拥挤的超球体以被选为敌人。下图表示上述两个选择过程的例子。覆盖所有子超球体的主超球体没有在该图中示出。
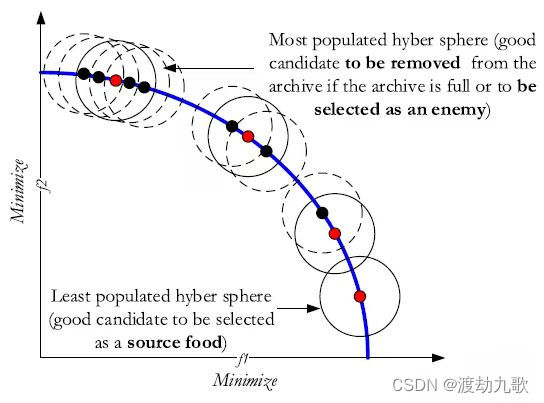
MODA算法的所有参数都与DA相同,除了两个新的参数用于定义超球体的最大数量和档案大小。
二、MODA的伪代码

三、多目标蜻蜓算法(MODA)Matlab代码
clc;
clear;
close all;
%% 多目标目标函数
ObjectiveFunction=@ZDT1;
dim=5;
lb=0;
ub=1;
obj_no=2;
if size(ub,2)==1ub=ones(1,dim)*ub;lb=ones(1,dim)*lb;
end
%% 初始化多目标蜻蜓优化算法参数
max_iter=100;
N=100;
ArchiveMaxSize=100;
Archive_X=zeros(100,dim);
Archive_F=ones(100,obj_no)*inf;
Archive_member_no=0;
r=(ub-lb)/2;
V_max=(ub(1)-lb(1))/10;
Food_fitness=inf*ones(1,obj_no);
Food_pos=zeros(dim,1);
Enemy_fitness=-inf*ones(1,obj_no);
Enemy_pos=zeros(dim,1);
X=initialization(N,dim,ub,lb);
fitness=zeros(N,2);
DeltaX=initialization(N,dim,ub,lb);
iter=0;
position_history=zeros(N,max_iter,dim);
for iter=1:max_iterr=(ub-lb)/4+((ub-lb)*(iter/max_iter)*2);w=0.9-iter*((0.9-0.2)/max_iter);my_c=0.1-iter*((0.1-0)/(max_iter/2));if my_c<0my_c=0;endif iter<(3*max_iter/4)s=my_c; % 分离权重a=my_c; %对齐权重c=my_c; % 聚集权重f=2*rand; % 食物吸引权重e=my_c; % 天敌驱散权重elses=my_c/iter; a=my_c/iter; c=my_c/iter; f=2*rand; e=my_c/iter; end%% 首先计算所有的目标值for i=1:N Particles_F(i,:)=ObjectiveFunction(X(:,i)');if dominates(Particles_F(i,:),Food_fitness)Food_fitness=Particles_F(i,:);Food_pos=X(:,i);endif dominates(Enemy_fitness,Particles_F(i,:))if all(X(:,i)<ub') && all( X(:,i)>lb')Enemy_fitness=Particles_F(i,:);Enemy_pos=X(:,i);endendend[Archive_X, Archive_F, Archive_member_no]=UpdateArchive(Archive_X, Archive_F, X, Particles_F, Archive_member_no);if Archive_member_no>ArchiveMaxSizeArchive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);[Archive_X, Archive_F, Archive_mem_ranks, Archive_member_no]=HandleFullArchive(Archive_X, Archive_F, Archive_member_no, Archive_mem_ranks, ArchiveMaxSize);elseArchive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);endArchive_mem_ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no);%% 提高复盖率的食物(选择种群最少地区的归档成员以提高复盖率的食物)index=RouletteWheelSelection(1./Archive_mem_ranks);if index==-1index=1;endFood_fitness=Archive_F(index,:);Food_pos=Archive_X(index,:)';%% (提高复盖率)选择种群最多的地区的档案成员作为敌人来提高复盖率index=RouletteWheelSelection(Archive_mem_ranks);if index==-1index=1;endEnemy_fitness=Archive_F(index,:);Enemy_pos=Archive_X(index,:)';for i=1:Nindex=0;neighbours_no=0;clear Neighbours_Vclear Neighbours_X%% 找到附近的解决方案for j=1:NDist=distance(X(:,i),X(:,j));if (all(Dist<=r) && all(Dist~=0))index=index+1;neighbours_no=neighbours_no+1;Neighbours_V(:,index)=DeltaX(:,j);Neighbours_X(:,index)=X(:,j);endend%% 分离S=zeros(dim,1);if neighbours_no>1for k=1:neighbours_noS=S+(Neighbours_X(:,k)-X(:,i));endS=-S;elseS=zeros(dim,1);end%% 对齐if neighbours_no>1A=(sum(Neighbours_V')')/neighbours_no;elseA=DeltaX(:,i);end%% 聚集if neighbours_no>1C_temp=(sum(Neighbours_X')')/neighbours_no;elseC_temp=X(:,i);endC=C_temp-X(:,i);%% 食物吸引Dist2Attraction=distance(X(:,i),Food_pos(:,1));if all(Dist2Attraction<=r)F=Food_pos-X(:,i);iter;elseF=0;end%% 天敌驱散Dist=distance(X(:,i),Enemy_pos(:,1));if all(Dist<=r)E=Enemy_pos+X(:,i);elseE=zeros(dim,1);endfor tt=1:dimif X(tt,i)>ub(tt)X(tt,i)=lb(tt);DeltaX(tt,i)=rand;endif X(tt,i)<lb(tt)X(tt,i)=ub(tt);DeltaX(tt,i)=rand;endendif any(Dist2Attraction>r)if neighbours_no>1for j=1:dimDeltaX(j,i)=w*DeltaX(j,i)+rand*A(j,1)+rand*C(j,1)+rand*S(j,1);if DeltaX(j,i)>V_maxDeltaX(j,i)=V_max;endif DeltaX(j,i)<-V_maxDeltaX(j,i)=-V_max;endX(j,i)=X(j,i)+DeltaX(j,i);endelseX(:,i)=X(:,i)+Levy(dim)'.*X(:,i);DeltaX(:,i)=0;endelse for j=1:dimDeltaX(j,i)=s*S(j,1)+a*A(j,1)+c*C(j,1)+f*F(j,1)+e*E(j,1) + w*DeltaX(j,i);if DeltaX(j,i)>V_maxDeltaX(j,i)=V_max;endif DeltaX(j,i)<-V_maxDeltaX(j,i)=-V_max;endX(j,i)=X(j,i)+DeltaX(j,i);endendFlag4ub=X(:,i)>ub';Flag4lb=X(:,i)<lb';X(:,i)=(X(:,i).*(~(Flag4ub+Flag4lb)))+ub'.*Flag4ub+lb'.*Flag4lb;enddisplay(['在迭代时 ', num2str(iter), '有 ', num2str(Archive_member_no), ' 非支配解决方案']);
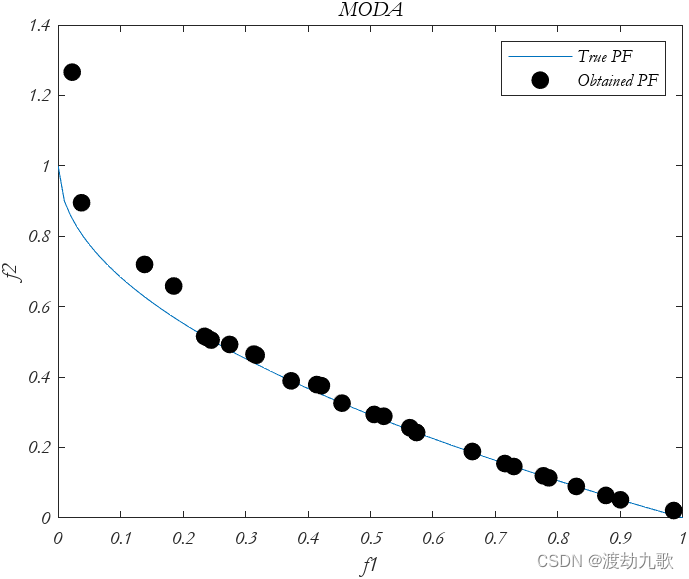
endfigureDraw_ZDT1();hold on
if obj_no==2plot(Archive_F(:,1),Archive_F(:,2),'ko','MarkerSize',8,'markerfacecolor','k');
elseplot3(Archive_F(:,1),Archive_F(:,2),Archive_F(:,3),'ko','MarkerSize',8,'markerfacecolor','k');
end
legend('True PF','Obtained PF');
title('MODA');
%======目标函数===========function o = ZDT1(x)o = [0, 0];dim = length(x);
g = 1 + 9*sum(x(2:dim))/(dim-1);o(1) = x(1);
o(2) = g*(1-sqrt(x(1)/g));
end
function [Archive_X_updated, Archive_F_updated, Archive_member_no]=UpdateArchive(Archive_X, Archive_F, Particles_X, Particles_F, Archive_member_no)
Archive_X_temp=[Archive_X ; Particles_X'];
Archive_F_temp=[Archive_F ; Particles_F];o=zeros(1,size(Archive_F_temp,1));for i=1:size(Archive_F_temp,1)o(i)=0;for j=1:i-1if any(Archive_F_temp(i,:) ~= Archive_F_temp(j,:))if dominates(Archive_F_temp(i,:),Archive_F_temp(j,:))o(j)=1;elseif dominates(Archive_F_temp(j,:),Archive_F_temp(i,:))o(i)=1;break;endelseo(j)=1;o(i)=1;endend
endArchive_member_no=0;
index=0;
for i=1:size(Archive_X_temp,1)if o(i)==0Archive_member_no=Archive_member_no+1;Archive_X_updated(Archive_member_no,:)=Archive_X_temp(i,:);Archive_F_updated(Archive_member_no,:)=Archive_F_temp(i,:);elseindex=index+1;end
endend
function o = RouletteWheelSelection(weights)
accumulation = cumsum(weights);
p = rand() * accumulation(end);
chosen_index = -1;
for index = 1 : length(accumulation)if (accumulation(index) > p)chosen_index = index;break;end
end
o = chosen_index;
end
function ranks=RankingProcess(Archive_F, ArchiveMaxSize, obj_no)my_min=min(Archive_F);
my_max=max(Archive_F);if size(Archive_F,1)==1my_min=Archive_F;my_max=Archive_F;
endr=(my_max-my_min)/(20);ranks=zeros(1,size(Archive_F,1));for i=1:size(Archive_F,1)ranks(i)=0;for j=1:size(Archive_F,1)flag=0; % 一个标志,以查看该点是否在所有维度上都在新区域中。for k=1:obj_noif (abs(Archive_F(j,k)-Archive_F(i,k))<r(k))flag=flag+1;endendif flag==obj_noranks(i)=ranks(i)+1;endend
end
end
function o=Levy(d)beta=3/2;sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;
v=randn(1,d);
step=u./abs(v).^(1/beta);o=0.01*step;
end
%% 初始化
function X=initialization(SearchAgents_no,dim,ub,lb)Boundary_no= size(ub,2); % 边界数%% 如果所有变量的边界相等,用户对ub和lb都输入一个标志号
if Boundary_no==1ub_new=ones(1,dim)*ub;lb_new=ones(1,dim)*lb;
elseub_new=ub;lb_new=lb;
end%% 如果每个变量具有不同的lb和ub
for i=1:dimub_i=ub_new(i);lb_i=lb_new(i);X(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
endX=X';
end
function [Archive_X_Chopped, Archive_F_Chopped, Archive_mem_ranks_updated, Archive_member_no]=HandleFullArchive(Archive_X, Archive_F, Archive_member_no, Archive_mem_ranks, ArchiveMaxSize)for i=1:size(Archive_F,1)-ArchiveMaxSizeindex=RouletteWheelSelection(Archive_mem_ranks);Archive_X=[Archive_X(1:index-1,:) ; Archive_X(index+1:Archive_member_no,:)];Archive_F=[Archive_F(1:index-1,:) ; Archive_F(index+1:Archive_member_no,:)];Archive_mem_ranks=[Archive_mem_ranks(1:index-1) Archive_mem_ranks(index+1:Archive_member_no)];Archive_member_no=Archive_member_no-1;
end
Archive_X_Chopped=Archive_X;
Archive_F_Chopped=Archive_F;
Archive_mem_ranks_updated=Archive_mem_ranks;
endfunction TPF=Draw_ZDT1()
%====TPF是真正的帕累托最优前沿=====
addpath('ZDT_set')
ObjectiveFunction=@(x) ZDT1(x);
x=0:0.01:1;
for i=1:size(x,2)TPF(i,:)=ObjectiveFunction([x(i) 0 0 0]);
end
line(TPF(:,1),TPF(:,2));
title('ZDT1')
xlabel('f1')
ylabel('f2')
box on
fig=gcf;
set(findall(fig,'-property','FontName'),'FontName','Garamond')
set(findall(fig,'-property','FontAngle'),'FontAngle','italic')
endfunction o=dominates(x,y)
o=all(x<=y) && any(x<y);
endfunction o = distance(a,b)
for i=1:size(a,1)o(1,i)=sqrt((a(i)-b(i))^2);
end
end四、运行结果
这篇关于多目标蜻蜓算法(MODA)附Matlab代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





